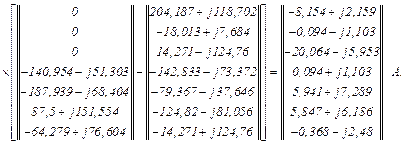Формалізовані методи розрахунку усталених
Режимів в електричних колах
Методичні вказівки
до практичних занять та лабораторних робіт
з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” для студентів електроенергетичних спеціальностей
Затверджено на засіданні
кафедри «Електричні станції»
Протокол № 1 від 28 серпня 2013 р.
Львів 2014
Формалізовані методи розрахунку усталених режимів в електричних колах. Методичні вказівки до практичних занять та лабораторних робіт з дисциплін “Математичне моделювання в електроенергетиці” та “Математичні моделі в електротехніці” / Укл. М.С. Сегеда, Т.А. Мазур – Львів: Національний університет “Львівська політехніка”, 2014. – 44 с.
Укладачі: Сегеда М.С., професор, доктор техн. наук
Мазур Т.А., асистент
Відповідальний за випуск: Сегеда М.С., професор, доктор техн. наук
Рецензенти: Варецький Ю.О., професор, доктор техн. наук
Гоголюк П.Ф., доцент, канд. техн. наук
Мета роботи: вивчення формалізованих методів аналізу електричних кіл, оволодіти навиками використання системи символьної математики МаthCad.
Основні відомості
Використання теорії графів, матрично-векторної алгебри, а також методів аналізу електричних кіл під час дослідження електромагнетних процесів у ЕЕС дає змогу створювати цифрові моделі, які працюють автоматично. Такий підхід забезпечує автоматичне формування та розв’язання рівнянь стану ЕЕС.
Найширше застосовуються під час дослідження електромагнетних процесів у ЕЕС методи аналізу електричних кіл, складених із двополюсників. Як було показано в розділі 2, використовуючи теорію графів і теорію множин, можна аналітично описати структурні елементи та фізичні величини електричного кола.
Основними фізичними величинами електричного кола є параметри заступної схеми та координати режиму. До параметрів заступної схеми електричного кола належать – імпеданс (комплексний опір), складовими якого є резистанс (активний опір), реактанс (реактивний опір); адмітанс (комплексна провідність), яка складається з кондуктансу (активної провідності), сусцептансу (реактивної провідності). До координат режиму чи процесу (фізичні величини, які змінюються в часі) належать джерело ЕРС, джерело струму, струм, напруга, заряд, магнетний потік, напруженість електричного та магнетного полів тощо. У деяких джерелах координати режиму називають ще параметрами режиму чи змінними стану.
Приклади розрахунку
для схеми, зображеної на рис. 1, обчислити струми та напруги віток електричного кола на підставі: - законів Ома та Кірхгофа; - вузлових та контурних рівнянь у координатах струмів та напруги віток; - методом незалежних струмів; - методом контурних струмів; - методом незалежних напруг; - методом вузлових напруг; - методом міжвузлових напруг; - методом координат віток; методом визначальних координат.
Рис. 1. Схема електричного кола
Дано: 
Схема має 
віток, 
вузлів, 
електрично не зв’язаних схем, а між опорами віток 
і 
є взаємоіндуктивний зв’язок. Граф схеми електричного кола наведено на рис. 2.
Рис. 2. Граф заступної схеми електричного кола
Серед вершин графа вузол 
є елементарним. Вузли 
і 
приймаємо за базові.
Приклад 1. Аналіз електричного кола на підставі законів Ома та Кірхгофа
Розв’язання.
Запишемо у матрично-векторній формі рівняння законів Ома та Кірхгофа
Граф схеми електричного кола (рис. 1) показано на рис. 2. Формуємо матриці, які описують структуру, параметри та координати електричного кола:
– перша матриця інциденцій
– друга матриця інциденцій
– матриця імпедансів
– вектор ЕРС
– вектор джерел струму
Відповідно формуються вектори струмів та напруг віток, тобто
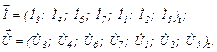
Формуємо блочне матрично-векторне рівняння
Використовуючи систему символьної математики MathCad, розв’язуємо одержане блочне матрично-векторне рівняння і отримуємо напруги та струми віток, тобто
|
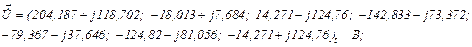
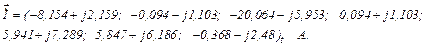
► Приклад 2. Аналіз електричного кола на підставі вузлових і контурних рівнянь
Розв’язання.
Запишемо у матрично-векторній формі рівняння законів Ома та Кірхгофа
Граф схеми електричного кола (рис. 1) показано на рис. 2. Формуємо матриці, які описують структуру, параметри та координати електричного кола:
– перша матриця інциденцій
– друга матриця інциденцій
– матриця імпедансів
– вектор ЕРС
– вектор джерел струму
Відповідно формуються вектори струмів та напруг віток, тобто
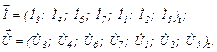
Формуємо блочне матрично-векторне рівняння
Використовуючи систему символьної математики MathCad, розв’язуємо одержане блочне матрично-векторне рівняння і отримуємо напруги та струми віток, тобто
|
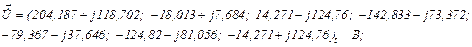
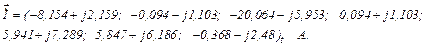
► Приклад 3. Аналіз електричного кола на підставі вузлових
і контурних рівнянь в координатах струмів віток
Розв’язання.
Запишемо матрично-векторні вузлові та контурні рівняння у координатах струмів віток у блочній формі
Граф схеми електричного кола (рис. 1) показано на рис. 2. Формуємо матриці, які описують структуру, параметри та координати електричного кола:
– перша матриця інциденцій
– друга матриця інциденцій
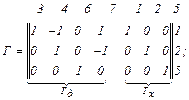
– матриця імпедансів
– вектор ЕРС
– вектор джерел струму
Відповідно формуються вектори струмів та напруг віток, тобто
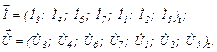
Формуємо контурні матриці опорів та ЕРС
Формуємо блочне матрично-векторне рівняння
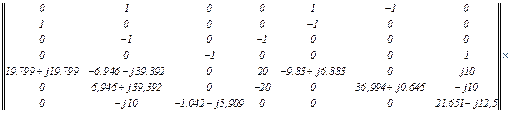
Використовуючи систему символьної математики MathCad, розв’язуємо одержане блочне матрично-векторне рівняння й отримуємо струми віток, тобто
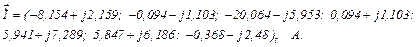
Напругу віток обчислюємо на підставі рівняння віток
|
► Приклад 4. Аналіз електричного кола на підставі вузлових і контурних рівнянь в координатах напруг віток
Розв’язання.
Запишемо матрично-векторні вузлові та контурні рівняння в координатах напруг віток у блочній формі
Граф схеми електричного кола (рис. 1) показано на рис. 2. Формуємо матриці, які описують структуру, параметри та координати електричного кола:
– перша матриця інциденцій
– друга матриця інциденцій
– матриця імпедансів
– матриця адмітансів
– вектор ЕРС
– вектор джерел струму
Відповідно формуються вектори струмів та напруг віток, тобто
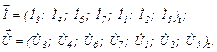
Формуємо матрицю перетворення ЕРС в еквівалентні ДС
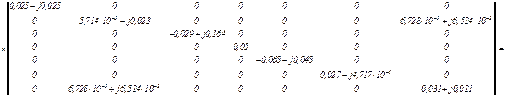
Формуємо праву частину блочного матрично-векторного рівняння, тобто
Формуємо блочне матрично-векторне рівняння
Використовуючи систему символьної математики MathCad, розв’язуємо одержане блочне матрично-векторне рівняння й отримуємо напруги віток, тобто
Струми віток обчислюємо на підставі рівняння віток
|
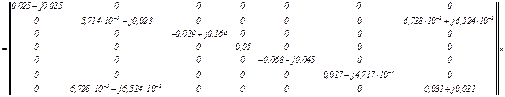
