Рассмотрим СЛАУ:
 ~ ~ 
| (7.1) |
По аналогии со СЛАУ второго порядка выпишем  ,
,  ,
, 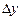 и
и  .
.
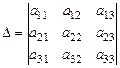 , ,  , ,
 , , 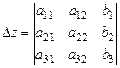 . .
| (7.2) |
Тогда получим:
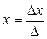 ; ;  ; ;  . .
| (7.3) |
Пример №7.1:
Решите систему линейных алгебраических уравнений третьего порядка методом Крамера.

Решение:
Решим данную СЛАУ методом Крамера. Для этого выпишем сначала расширенную матрицу этой:
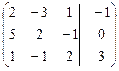
Далее воспользуемся формулами Крамера (7.2):

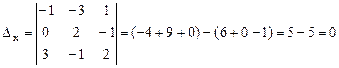


Тогда используя формулы (7.3) получим:
 ;
;
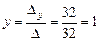 ;
;
 .
.
Ответ:  ,
,  ,
,  .
.
Решение СЛАУ методом Гаусса.
Рассмотрим СЛАУ:
 ~
~ 
Метод Гаусса это итерационный метод решения СЛАУ. Эти итерации основаны на равносильных преобразованиях СЛАУ. Для того чтобы дать представление о равносильных преобразованиях систем сформулируем несколько определений и правил. Для определенности перечисленные определения и понятия дадим для случая трех переменных.
Определение №1: Равенство  будем называть линейным уравнением с тремя неизвестными.
будем называть линейным уравнением с тремя неизвестными.
Пусть  , тогда
, тогда  , тоже линейное уравнение с тремя неизвестными.
, тоже линейное уравнение с тремя неизвестными.
Определение №2: Два линейных уравнения с тремя неизвестными  и
и  называются равносильными, если каждое решение
называются равносильными, если каждое решение  первого есть решение второго, а каждое решение
первого есть решение второго, а каждое решение  второго есть решение первого. При этом пишут:
второго есть решение первого. При этом пишут:  .
.
Правило равносильных преобразований систем.
Дадим несколько основных правил равносильных преобразований СЛАУ. Для простоты будем говорить о СЛАУ третьего порядка. Заметим, что все правила перечисленные здесь для СЛАУ третьего порядка справедливы и для СЛАУ второго порядка и порядка большего трех.
8.2.1°. Если в СЛАУ одно уравнение заменить на равносильное ему уравнение, то получим систему, равносильную данной.
8.2.2°. Система содержит уравнение вида  , где
, где  – некоторое неизвестное,
– некоторое неизвестное,  – функция, не зависящая от
– функция, не зависящая от  . Тогда, если во всех оставшихся уравнениях СЛАУ вместо
. Тогда, если во всех оставшихся уравнениях СЛАУ вместо  подставить
подставить  , то полученная таким образом система будет равносильна исходной.
, то полученная таким образом система будет равносильна исходной.
8.2.3°. Допустим, что СЛАУ содержащей уравнение 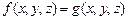 и
и  . Если в этой СЛАУ уравнение
. Если в этой СЛАУ уравнение 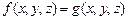 заменить уравнением
заменить уравнением  , где
, где  , то получим систему, равносильную данной.
, то получим систему, равносильную данной.
Метод Гаусса.
Опишем теперь сам алгоритм метода Гаусса для нахождения решения СЛАУ.
1. Выписать расширенную матрицу СЛАУ.
2. В таблице в первом столбце выбрать ведущий элемент и эту строку поменять местами с первой строкой таблицы.
3. С помощью правил 3° сделать так, чтобы элементы выбранного столбца под ведущим элементом обратились в ноль.
4. Выбрать ведущий элемент в следующем столбце и поменять строку с выбранным элементом со строкой, стоящей ниже строки с прошлым выбранным элементом и снова повторить п.3, продолжая делать это, пока таблица не примет один из видов:
а. 1) В одной из строк все элементы  , а
, а 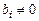
 система решений не имеет.
система решений не имеет.
б. 2) Если в одной из строк все  и
и  , то поменять эту строку с самой нижней строкой, в которой хотя бы одно
, то поменять эту строку с самой нижней строкой, в которой хотя бы одно 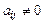 и снова перейти к п.3. Когда исчерпаются все такие строки, принимая неизвестные, которые находятся в конце таблицы, за независимые функции, по правилу 8.2.20, найдем решение СЛАУ. Заметим, число таких неизвестных равно числу нулевых строк. В этом случаи СЛАУ имеет бесконечное множество решений.
и снова перейти к п.3. Когда исчерпаются все такие строки, принимая неизвестные, которые находятся в конце таблицы, за независимые функции, по правилу 8.2.20, найдем решение СЛАУ. Заметим, число таких неизвестных равно числу нулевых строк. В этом случаи СЛАУ имеет бесконечное множество решений.
3) Если мы получим таблицу вида (в частности):

Тогда, используя правило 8.2.2°, получим, что 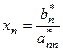 . Подставляя, полученный
. Подставляя, полученный  в строку выше, снова используя правило 8.2.2°, найдем
в строку выше, снова используя правило 8.2.2°, найдем  . Продолжая этот процесс далее, последовательно найдем оставшиеся
. Продолжая этот процесс далее, последовательно найдем оставшиеся 
 . Очевидно, что в этом случаи СЛАУ имеет единственное решение.
. Очевидно, что в этом случаи СЛАУ имеет единственное решение.
Пример №8.3.1:
Решите систему линейных алгебраических уравнений третьего методом Гаусса.

Решение:
Решим данную систему методом Гаусса. Для этого выпишем сначала расширенную матрицу этой:
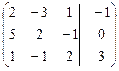
Далее начнем производить шаги метода Гаусса. Ведущий элемент будем обозначать квадратиком. Строки будем обозначать буквой С, а действия производимые над строками будем писать правее матрицы.



Сопоставив последней расширенной матрице СЛАУ, получим

Заметим, что решение данной СЛАУ, полученное с помощью метода Гаусса, совпадает с решением, полученным с помощью метода Крамера.
Ответ:  ,
,  ,
,  .
.
9 Решение систем двух уравнений с двумя неизвестными, когда одно линейное, а другое – второй степени.
Запишем еще одно правило равносильного преобразования систем:
9.4°. Система, содержащая уравнение вида  , распадается на две системы: в одной это уравнение заменено на
, распадается на две системы: в одной это уравнение заменено на  , а в другой – уравнением
, а в другой – уравнением  . При этом, если уравнение
. При этом, если уравнение  равносильно совокупности уравнений
равносильно совокупности уравнений  и
и  , то данная система равносильна совокупности этих систем, то есть множество решений данной системы есть объединение множеств решений этих систем.
, то данная система равносильна совокупности этих систем, то есть множество решений данной системы есть объединение множеств решений этих систем.
Пример №9.1:
Решить систему уравнений

Решение:
Для решения данной системы применим сначала правило 8.2.2о, тогда получим
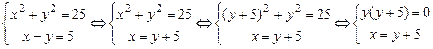
Применив к последней системе правило 9.4о получим

Ответ: (5;0) и (0;-5).
10 Практические задания
1. По заданной системе линейных алгебраических уравнений постройте ее расширенную матрицу:
1.1  1.2
1.2 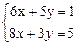 1.3
1.3 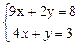
1.4  1.5
1.5  1.6
1.6 
1.7  1.8
1.8  1.9
1.9 
1.10  1.11
1.11  1.12
1.12 
1.13  1.14
1.14  1.15
1.15 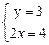
1.16  1.17
1.17  1.18
1.18 
1.19  1.20
1.20  1.21
1.21 
1.22  1.23
1.23 
2. Найдите значение определителя методом разложения и графическим методом. Сравните результаты.
2.1 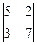 2.2
2.2  2.3
2.3 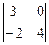 2.4
2.4 
2.5  2.6
2.6  2.7
2.7  2.8
2.8 
2.9  2.10
2.10  2.11
2.11 
2.12  2.13
2.13  2.14
2.14 
2.15  2.16
2.16 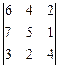 2.17
2.17 
2.18 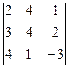 2.19
2.19  2.20
2.20 
2.21  2.22
2.22 
3. Найдите корни уравнения:
3.1  3.2
3.2 
3.3  3.4
3.4 
3.5 
3.6  3.7
3.7 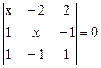
3.8 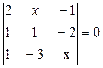 3.9
3.9 
3.10 
4. Приведите уравнения к каноническому уравнению эллипса, гиперболы, параболы или окружности и найдите для кривых второго порядка заданных данными уравнениями оси, фокусы, асимптоты, директрису и эксцентриситет:
4.1  4.2
4.2 
4.3  4.4
4.4

4.5 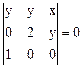 4.6
4.6 
4.7 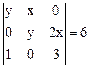 4.8
4.8 
5. Решите систему линейных уравнений методом подстановки, методом Крамера и методом Гаусса:
5.1  5.2
5.2 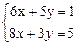 5.3
5.3 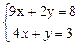
5.4  5.5
5.5  5.6
5.6 
5.7  5.8
5.8  5.9
5.9 
5.10  5.11
5.11  5.12
5.12 
5.13  5.14
5.14  5.15
5.15 
5.16  5.17
5.17  5.18
5.18 
6. Найдите все значение параметра, при котором система алгебраических уравнений имеет единственное решение, бесконечно много решений и является несовместной:
6.1  6.2
6.2  6.3
6.3 
6.4 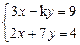 6.5
6.5  6.6
6.6 
6.7 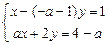 6.8
6.8  6.9
6.9 
6.10 
7. Решите систему уравнений
7.1  7.2
7.2  7.3
7.3 
7.4  7.5
7.5 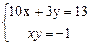 7.6
7.6 
7.7 






