Else ОПЕРАТОР,
End
Краткая форма
If ЛВ then ОПЕРАТОР1
End
Здесь
ЛВ, ЛВ1, ЛВ2, ЛВ3 – логические выражения;
ОПЕРАТОР1, ОПЕРАТОР2, ОПЕРАТОР– любые операторы или группы операторов языка Scilab.
Разделителями в операторах могут быть запятая или точка с запятой. Если ОПЕРАТОР расположен в следующей строке, то разделитель ставить не обязательно.
Порядок выполнения оператора условия следующий.
Полная форма 1
- Логическое выражение вычисляется до константы (0 или 1).
- Если логическое выражение истинно, то выполняется оператор, стоящий после слова then, а затем следующий за оператором if оператор.
- Если логическое выражение ложно, то выполняется оператор, стоящий после слова else, а затем следующий за оператором if оператор.
Краткая форма
- Логическое выражение вычисляется до константы (0 или 1).
- Если логическое выражение истинно, то выполняется оператор, стоящий после слова then, а затем следующий за оператором if оператор.
- Если логическое выражение ложно, то выполняется следующий за оператором if оператор.
При программировании логических выражений используются следующие операции отношения и логические операции.
| Название | Знак операции | Пример |
| Равно | == | x==y |
| Не равно | ~= | x~=y |
| Меньше | < | x<y |
| Больше | > | x>y |
| Меньше или равно | <= | x<=y |
| Больше или равно | >= | x>=y |
| Логическое И | & | x&y |
| Логическое ИЛИ | | | x|y |
| Логическое НЕ | ~ | ~x |
В простых логических выражениях используется знак операции отношения, например: a > b или c <= 5.8. В сложных логических выражениях используются знаки логических операций, например:
a>b | b<0
(a > 0) & (b>0)
Ниже приведен фрагмент программы, в котором с помощью оператора if в командную область выводится либо символьная константа "корни мнимые" либо "корни вещественные" в зависимости от того отрицателен ли результат арифметического выражения
b^2 - 4*a*c.
if b^2 - 4*a*c < 0 then disp("корни мнимые") else disp("корни вещественные")endОператоры цикла предназначены для программирования циклических алгоритмов, они изменяют естественный ход выполнения программы и относятся к операторам управления. Операторы являются взаимозаменяемыми, выбор для применения того или иного оператора зависит от программиста.
Операторы цикла в Scilab можно классифицировать следующим образом:
- оператор цикла с параметрами for;
- оператор цикла с предусловием while.
При классификации циклических алгоритмов отмечалось, что цикл может управляться явно выраженной переменной цикла, имеющей параметры, либо цикл не содержит переменной цикла и управляется иным способом.Операторы цикла можно разделить по тому же принципу:
- для программирования циклов с переменной цикла и параметрами;
- для программирования циклов без явно выраженной переменной цикла.
Оператор цикла for предназначен для программирования циклических алгоритмов, когда переменная цикла явно выражена и изменяется от начального значения до конечного значения с постоянным шагом.
Общий вид оператора цикла for
for x= xn: dx: xk
ОПЕРАТОР,
End
Здесь:
x – переменная цикла,
xn – начальное значение переменной цикла,
dx – шаг изменения переменной цикла,
xk – конечное значение переменной цикла,
ОПЕРАТОР – любой оператор или группа операторов рабочей части цикла.
Порядок выполнения оператора цикла:
- проверяется условие xn<=xk;
- если условие не выполняется, то оператор цикла прекращает свою работу, и выполняется следующий за ним оператор программы;
- если условие выполняется, то переменной цикла присваивается ее начальное значение x=xn;
- выполняется оператор рабочей части цикла;
- до тех пор, пока x< = xk переменная цикла увеличивается на шаг dx и выполняется рабочая часть цикла.
Количество повторений цикла вычисляется по формуле:
|xk – xn|/dx +1.
Примеры правильной записи оператора for:
| Фрагмент программы for k=1: 5 disp(k) end | Командное окно |
Оператор while предназначен для программирования любых циклов, где проверка условия повторения цикла выполняется перед выполнением рабочей части цикла.
Общий вид:
While ЛВ,
ОПЕРАТОР,
End
где
ЛВ – логическое выражение,
ОПЕРАТОР – любой оператор или группа операторов рабочей части цикла.
Порядок выполнения оператора следующий:
- проверяется истинность логического выражения;
- до тех пор, пока оно истинно, выполняется оператор рабочей части цикла;
- если логическое выражение стало ложным, то выполняется следующий за оператором цикла оператор программы.
Если логическое выражение в заголовке цикла while заведомо ложно, то цикл может не выполниться ни разу.
Примеры правильной записи оператора цикла while приведены ниже.
Вывести на экран дисплея четные целые числа от 2 до 12.
k=2;
while k<=20
Disp(k)
k=k+2;
End
Практическая часть
Задание 1. Программирование разветвляющихся алгоритмов
Постановка задачи. Разработать программу для формирования функции y(x). Подобрать набор тестов для проверки правильности работы программного фрагмента. Вычислить значения функции y(x) для тестовых значений x.
| Вид функции |

|
Порядок составления программы таков.
Шаг 1. Программируем ввод исходного данного – переменной х с использованием оператора ввода input.
Шаг 2. Проверяем, выполняется ли условие x > 20, и если оно выполнится, то программируем вычисление y=sqrt(x).
Шаг 3. Продолжаем оператор if, описывая, что будет в случае, если первое условие не выполняется. Для этого воспользуемся полной формой 2 и после elseif формируем второе условие в виде сложного логического выражения.
Шаг 4. Завершаем оператор if, указывая после else, чему равен результат в остальных случаях. Завершаем оператор if словом end.
Шаг 5. Выводим полученный результат в командную область.
| Программа | Результаты расчетов |
| x= input ("Задайте х=")if x>20 then y=sqrt(x), elseif (x>=1) & (x<=20) then y=x else y=4*x^2 enddisp('y=')disp(y) | Задайте х=25 y= 5. Задайте х=15 y= 15. Задайте х=-3 y= 36. |
Индивидуальные варианты приведены в таблице 2.7.
Таблица 2.7.
| № | Вид функции | № | Вид функции |
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 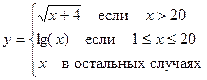
|
Задание 2. Программирование циклических алгоритмов
Постановка задачи. Задан вектор произвольной длины N. Разработать программу для вычисления результата по индивидуальному заданию. Проверить работу программы на тестовом примере (числовые значения вектора подобрать самостоятельно).
| Вычислить произведение отрицательных элементов вектора с четными номерами. |
Порядок составления программы таков.
Шаг 1. Программируем ввод исходного данного – вектора X с использованием оператора присваивания. Числа в векторе подбираем таким образом, чтобы встречались и отрицательные и положительные числа. Программа должна выделить отрицательные числа и найти их произведение.
Шаг 2. Для вычисления произведения выбираем переменную P, первоначально присваиваем ей значение 1.
Шаг 3. Для того, чтобы просмотреть элементы, имеющие в векторе четные номера, например, 2, 4, 6 и т.д., организуем цикл с переменной цикла i. Этой переменной первоначально присвоим значение 2, т.е. будем первоначально рассматривать второй элемент вектора.
Шаг 4. Цикл должен выполняться до тех пор, пока текущий номер элемента в векторе (переменная цикла i) меньше общего количества элементов. В данном векторе 10 элементов, поэтому заголовок цикла имеет вид: while i<=10.
Шаг 5. В цикле используется оператор if, чтобы проверить, является ли элемент вектора Х отрицательным, т.е. меньшим нуля. Если это условие выполняется, то переменную Р умножаем на этот элемент и результат помещаем в ту же самую переменную Р. Завершаем оператор if словом end.
Шаг 6. В цикле изменяем переменную цикла на 2 (i=i+2) и заканчиваем цикл словом end.
Шаг 7. Выводим элементы исходного вектора и полученный результат в командную область.
| Программа | Результаты расчетов |
| X=[-2 -3 -6 5 2 -4 8 9 -10 -7]P=1; i=2while i<=10 if X(i)<0 then P=P*X(i) end i=i+2enddisp(X); disp(P) | - 2. - 3. - 6. 5. 2. - 4. 8. 9. - 10. - 7. - 84. |
Индивидуальные варианты приведены в таблице 2.8.
Таблица 2.8.
| № | Условие задачи |
| 1. | Подсчитать количество элементов вектора, по значению принадлежащих интервалу [ 3,1…5,4] |
| 2. | Подсчитать количество отрицательных элементов вектора |
| 3. | Подсчитать сумму чисел, по значению меньших последнего элемента вектора |
| 4. | Подсчитать произведение чисел, по значению больших 7 |
| 5. | Подсчитать среднее арифметическое отрицательных элементов вектора |
| 6. | Подсчитать количество элементов вектора, по значению больших 5 и стоящих на нечетных местах |
| 7. | Подсчитать сумму квадратов положительных элементов вектора, стоящих на четных местах |
| 8. | Подсчитать количество элементов вектора, больших первого элемента |
| 9. | Подсчитать сумму элементов вектора, по значению принадлежащих интервалу [ 2,5…8,4] |
| 10. | Подсчитать количество чисел, больших последнего элемента вектора |
| 11. | Вычислить произведение положительных элементов вектора |
| 12. | Подсчитать сумму элементов вектора, больших 12 и стоящих на четных местах |
| 13. | Подсчитать произведение элементов вектора, меньших 4 и стоящих на нечетных местах |
| 14. | Подсчитать сумму отрицательных и стоящих на четных местах элементов вектора |
| 15. | Подсчитать среднее арифметическое положительных элементов вектора |






