Фирмы Ф 1 и Ф 2 производят однородный сезонный товар, пользующийся спросом в течение n единиц времени. Доход от продажи товара в единицу времени составляет С ден. ед. Фирма Ф 2, будучи более состоятельной, в ходе конкурентной борьбы стремится вытеснить фирму Ф 1 с рынка сбыта, способствуя своими действиями минимизации ее дохода, не считаясь при этом с временными потерями части своего дохода в надежде наверстать упущенное в будущем. Действующее законодательство не позволяет злоупотреблять для этого заведомым занижением цены на товар (прибегать к демпинговым ценам). Единственным допустимым способом достижения своей цели для фирмы Ф 2 (как и для фирмы Ф 1 в целях защиты своих интересов на рынке сбыта) остаются повышение качества товара и надлежащий выбор момента времени поставки его на рынок сбыта. Уровень спроса на товар зависит от его качества, и в данный момент реализуется тот товар, качество которого выше. Повышение же качества требует дополнительных затрат времени на совершенствование технологии его изготовления и переналадки оборудования. В связи с этим будем предполагать, что качество товара тем выше, чем позже он поступает на рынок. Придать описанной ситуации игровую схему и построить платежную матрицу. Дать рекомендации фирмам Ф 1 и Ф 2 по оптимальным срокам поставки товара на рынок сбыта, обеспечивающие фирме Ф 1 наибольший средний доход, а фирме Ф 2 – наименьшие потери.
Решение. Если фирма Ф 1 предложит свой товар в момент i, а фирма Ф 2 в момент j > i, то фирма Ф 1, не имея конкурента в течение (j - i) единиц времени, получит за этот период доход в C (j - i) ден. ед. В момент j на рынке появляется товар фирмы Ф 2 более высокого качества (ведь j > i!), и фирма Ф 1 теряет рынок и дохода не получает.
Если i > j, то фирма Ф 1, предлагая товар более высокого качества, будет единолично получать доход на отрезке от t до n, состоящем из (n - i + 1) единиц времени. Доход фирмы Ф 1 на нем будет равен С (n – i +1) ден. ед.
Наконец, если i = j, т. е. если на рынок одновременно поступает товар обеих фирм, то он реализуется с одинаковым спросом, а потому доход как фирмы Ф 1, так и фирмы Ф 2, будет составлять 0,5 С (n - i + 1) ден. ед.
А теперь формализуем рассмотренную ситуацию в терминах теории игр. Фирмы Ф 1 и Ф 2 примем соответственно за игроков А и В. Через 
обозначим чистую стратегию игрока А, состоящую в том, что он поставляет свой товар на рынок сбыта в i -ю единицу времени; через 
чистую стратегию игрока В, в соответствии с которой он поставляет свой товар для реализации в j -ю единицу времени. Игрок А, выбирая i -ю единицу времени поставки товара, стремится максимизировать свой доход, а игрок В, выбирая j -ю единицу времени поставки своего товара, преследует прямо противоположную цель – минимизировать доход игрока А. В этом проявляется антагонистичность конфликта между игроками.
Что же касается выигрышей aij игрока А, то ими будут величины дохода фирмы Ф 1, найденные нами выше для всех возможных случаев. Их можно компактно записать в виде следующей функции выигрыша игрока А:
(6.5)
Если, например, n = 5 и С = 1, то функцию выигрыша (6.5) можно записать в форме следующей платежной матрицы (табл. 6.2):
Таблица 6.2
| B j A i | B1 | B2 | B3 | B4 | B5 | ||
| A1 | 2,5 | ||||||
| A2 | |||||||
| A3 | 1,5 | ||||||
| A4 | |||||||
| A5 | 0,5 | ||||||
Найдем решение игры, заданной этой платежной матрицей. Поскольку 
, то решать игру в чистых стратегиях нельзя. Найдем оптимальные смешанные стратегии игроков.
Задача нахождения оптимальной смешанной стратегии 
игрока A сводится к задаче линейного программирования (6.1), (6.2). В нашем случае она примет вид
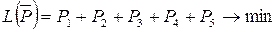
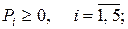
где Pi = pi / v,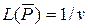 
.
Задача нахождения оптимальной смешанной стратегии 
игрока B сводится к задаче линейного программирования (6.3), (6.4). В нашем случае она примет вид
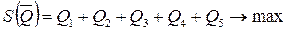
где Qi = pi / v.
