Процессы в цепи возбуждения электрических машины без учёта влияния реакции якоря, потоков рассеяния и вихревых токов можно описать следующими дифференциальными уравнениями:
UВ = IВ×RВ + WВ 
; (4.1)
ФВ = ¦(IВ), (4.2)
где UВ, IВ - соответственно напряжение и ток возбуждения;
RВ - суммарное сопротивление цепи возбуждения с учётом силовой цепи возбудителя;
WВ - суммарное число витков обмотки возбуждения;
ФВ - поток возбуждения;
¦(IВ) - нелинейная зависимость, не имеющая аналитического выражения, называемая кривой намагничивания электрической машины.
На рис. 4.1, приведена обобщённая кривая намагничивания двигателя в относительных единицах.
Рис. 4.1
Вводим оператор дифференцирования в уравнение (4.1)
UВ = IВ×RВ + WВ×ФВ×р. (4.1)
Отсюда
ФВ = 
. (4.2)
Преобразуем выражение за скобками в (4.2) к виду
= 
= 
,
где КВН = 
и ТВН = 
.
Соответственно коэффициент и электромагнитная постоянная времени цепи возбуждения электрической машины для спрямлённой характеристики намагничивания рис. 4.1 (прямая 2).
Тогда выражение (4.2) преобразуется к виду
ФВ = . (4.2)
На основе (4.2) и обратной кривой намагничивания
IВ = ¦1(ФВ) нелинейная цепь возбуждения может быть представлена структурной схемой вида (рис. 4.2).
Рис. 4.2
Если провести линейную аппроксимацию кривой намагничивания для какого-либо конкретного значения потока ФВ0, то структурная схема на рис. 4.2 может быть преобразована к виду (рис. 4.3).
Рис. 4.3
Здесь Кi = 
, причём DIВ и DФВ относительно небольшие приращения тока и потока возбуждения, полученные по кривой намагничивания в окрестности аппроксимируемой точки IВ0 (см. рис. 4.1). После эквивалентных преобразований структурная схема на рис. 4.3 может быть представлена на рис. 4.4.
Рис. 4.4
Здесь КВ = 
и ТВ = 
соответственно коэффициент и электромагнитная постоянная времени цепи возбуждения для выбранной точки аппроксимации. Очевидно, что по мере возрастания тока возбуждения растёт и величина коэффициента Кi, а это, в свою очередь, снижает значения КВ и ТВ по мере насыщения магнитной системы электрической машины.
Параметры исследуемой цепи возбуждения по вариантам приведены в таблице 4.1.
Таблица 4.1.
| № вар. | ||||||||||||
| парам. | ||||||||||||
| ФН, В×с | 0.146 | 0.2 | 0.11 | 0.12 | 0.16 | 0.18 | 0.22 | 0.2 | 0.18 | 0.16 | 0.14 | 0.12 |
| IВН, А | ||||||||||||
| RВ, Ом | 9.5 | 9.1 | 8.15 | 7.33 | 6.28 | 6.66 | 7.09 | 7.58 | 8.46 | 9.56 | 10.5 | |
| ТВН, с | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | 6.0 | 5.5 | 5.0 | 4.5 | 4.0 | 3.5 |
Внимание! До того, как приступить к выполнению лабораторной работы, необходимо рассчитать реальную кривую намагничивания двигателя для своего варианта, используя для этого рис. 4.1 и номинальные данные из таблицы. Кривая намагничивания моделируется с помощью блока Look-Up Table.
После этого рассчитать параметры и реализовать цифровую модель в соответствии со структурной схемой на рис. 4.2.
В отчёте по лабораторной работе необходимо:
1) проанализировать переходные процессы в цепи возбуждения, обусловленные изменением напряжения возбуждения DUВ = +0.1UВН при условии, что к обмотке возбуждения уже приложено напряжение UВ0 = 0.3UВН, 0.6UВН и 0.9UВН. Для того, чтобы исключить переходные процессы, связанные с приложением к обмотке возбуждения начального напряжения UВ0, необходимо в интегрирующем звене на модели задать начальное значение потока возбуждения, рассчитанное для этого режима с учётом кривой намагничивания;
2) для трех начальных значений протока возбуждения построить частотные характеристики (ЛАЧХ и ЛФЧХ), входной сигнал для частотной характеристики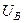 
, выходной 
.
3) по полученным кривым переходных процессов рассчитать значения КВ и ТВ для каждого режима;
4) построить зависимости КВ и ТВ от величины 
;
5) сделать выводы по полученным результатам.
Лабораторная работа № 5
