а) Замена ветви с несколькими источниками ЭДС ветвью с одной эквивалентной. ЭДС.
Условиями эквивалентности является равенство напряжений на зажимах (U ab, рис.13) исходной и эквивалентной ветвей, а также токов в ветвях.
 |
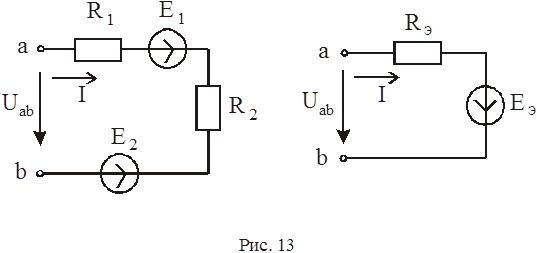Величины Е Э, R Э можно определить с помощью второго закона Кирхгофа. Так, для исходной ветви (рис. 13)
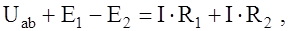
. (13)
для эквивалентной ветви
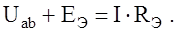
. (14)
Сравнивая выражения (13) и (14), получим
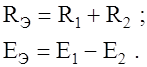
. (15)
Формула (15) получена с учетом того, что направление эквивалентной ЭДС выбрано совпадающим с направлением тока в цепи. Отсюда следует простое правило расчета Е Э: если направление ЭДС источника в исходной цепи (Е 1, рис.13) совпадает с направлением тока, то она входит в правую часть формулы (15) со знаком плюс, иначе - минус (Е 2, рис.13).
б) Замена параллельных ветвей, содержащих источники ЭДС и тока, одной эквивалентной.
 |
Эквивалентная ЭДС и сопротивление определяются по следующим формулам:
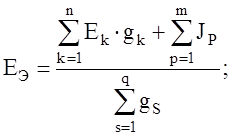
. (16)
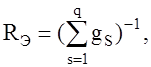
. (17)
где q – общее количество параллельных ветвей;
n – число ветвей, содержащих источники ЭДС;
m – число ветвей, содержащих источники тока.
В схеме (рис.14) направление эквивалентной ЭДС выбрано совпадающим с направлением тока. В этом случае знаки слагаемых в числителе формулы (16) можно определить по правилу: если направление ЭДС (источника тока) в исходной ветви совпадает с выбранным направлением эквивалентной ЭДС, то в числителе выражения (16) перед соответствующим слагаемым ставится знак плюс, иначе – минус.
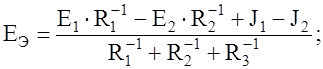
Так для схемы (рис.14)
 |
 |
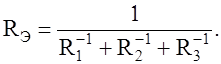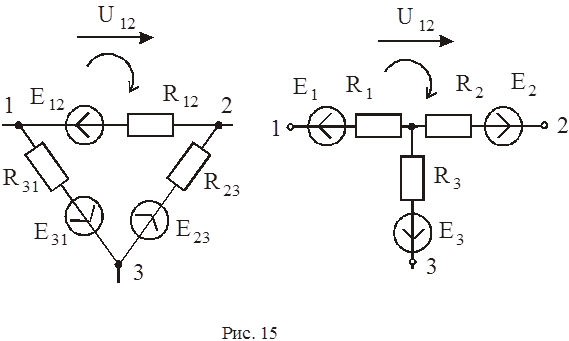в) Эквивалентные преобразования активных треугольника и звезды.
При преобразовании треугольник – звезда в ветвях эквивалентной звезды содержатся как пассивные элементы (сопротивления), так и активные (источники ЭДС). Величины эквивалентных ЭДС определяются из условия равенства разности потенциалов между соответствующими узлами до и после преобразования при полном отключении преобразуемого участка от остальной части цепи (рис.15). В этом случае во всех ветвях треугольника течет ток
/ (18)
а в ветвях звезды токи отсутствуют.
Запишем второй закон Кирхгофа для ветви R 12, E 12 треугольника:
 |
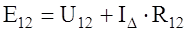и для звезды
 |
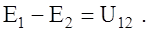Поскольку величины напряжений U12 в обеих схемах должны быть одинаковыми, получим
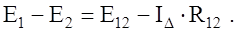
/ (19)
Аналогично для остальных ветвей имеем
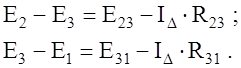/ (20)
/ (21)
Выражения (18) – (21) дают возможность определять величины эквивалентных ЭДС.
При переходе от треугольника к эквивалентной звезде с целью упрощения решаемой задачи величина ЭДС в одной из ветвей звезды может быть выбрана произвольно. Пусть, например, Е 3 = 0 тогда из выражения (20), (21) получим
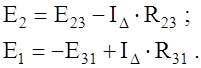/ (22)
/ (23)
При переходе от звезды к эквивалентному треугольнику в качестве дополнительного условия можно принять
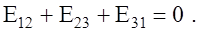
/ (24)
Тогда I ∆ = 0 и из (19) – (21) получим
.
.
.
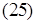
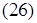
Величины эквивалентных сопротивлений звезды и треугольника определяются по формулам (7) – (12).
Рассмотрим, например схему (рис.16), которая при помощи преобразования звезды с ветвями (R 1, E 1), (R 2, E 2), (R 3, E 3) в эквивалентный треугольник получает вид
(рис.17).
Выберем в качестве дополнительного условия
тогда
 |
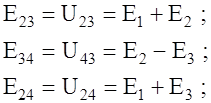
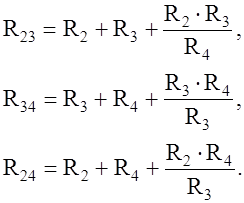Рассмотрим преобразование треугольника 1 2 3 (рис. 16) в эквивалентную звезду, для чего выделим его из цепи (рис. 18 а).
Ток треугольника
 |
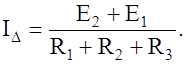Напряжения между узлами треугольника и звезды
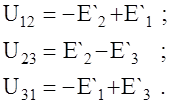
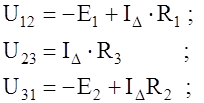
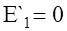
Принимаем для упрощения, тогда
 |
 |
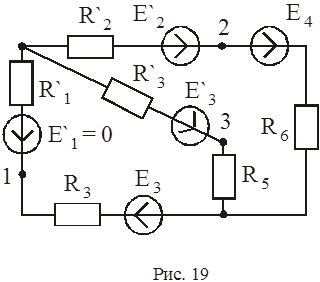В итоге схема (рис. 16) принимает вид, представленный на рис. 19.
ЗАДАНИЕ
Задача 1.
Определить эквивалентное сопротивление R Э (рис. 20, 21, 22) относительно указанных зажимов, если сопротивления равны 10 Ом.
 |
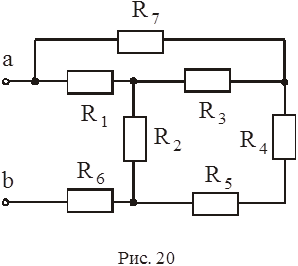Таблица 1
| № варианта | ||||||||||
| R7=0 | R4=¥ | R3=0 | R3=¥ | R1=0 | R1=¥ | R2=0 | R2=¥ | R4=0 R5=0 | R7=¥ |
 |
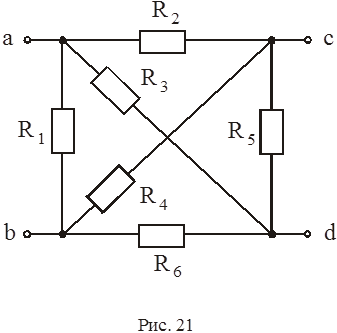Таблица 2
| № варианта | ||||||||||
| R5=0 Rab=? | R5=¥ Rab=? | R4=0 Rab=? | R3=0 Rcd=? | R3=0 Rac=? | R1=¥ Rbd=? | R5=0 Rac=? | R2=0 Rcd=? | R4=¥ Rad=? | R2=¥ Rbc=? |
 |
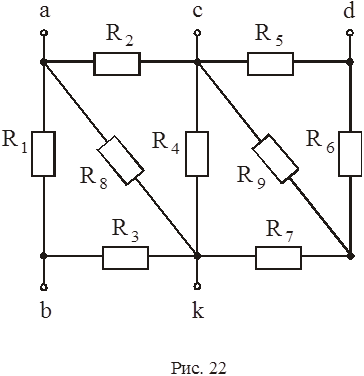Таблица 3
| № варианта | ||||||||||
| R9=0 Rab=? | R4=¥ Rab=? | R7=¥ Rab=? | R8=0 R9=0 Rbc=? | R8=¥ R9=0 Rac=? | R8=0 R9=¥ Rkd=? | R8=0 Rcd=? | R2=0 R7=0 Rcb=? | R6=¥ Rck=? | R3=¥ R8=0 Rak=? |
Задача 2.
Используя преобразования параллельных ветвей, упростить схему до трехконтурной. Составить уравнения по законам Кирхгофа для эквивалентной схемы.
Схемы к задаче 2:
 |
 |
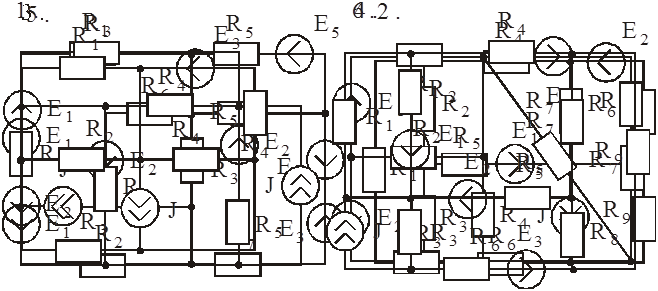Задача 3.
Используя взаимные преобразования активных треугольника и звезды, упростить схему до трехконтурной.
 |
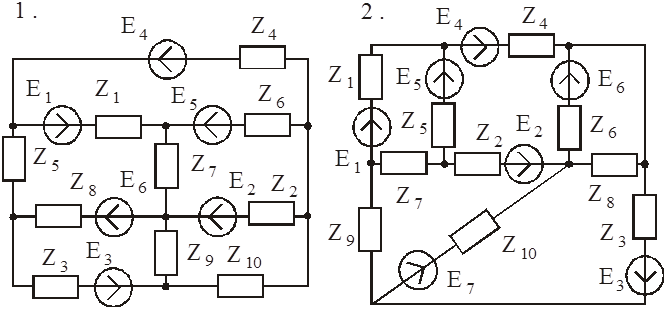Схемы к задаче 3:
 |
 |
 |
 |
 |
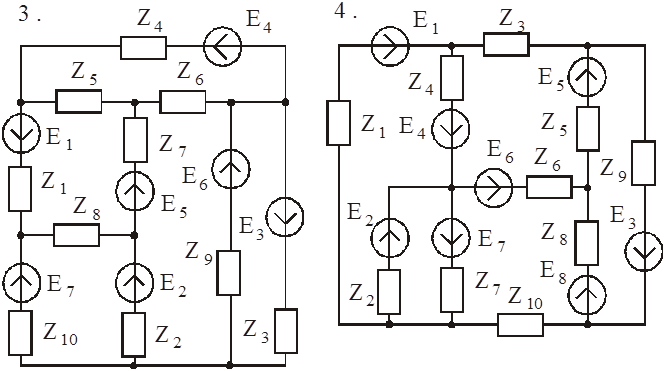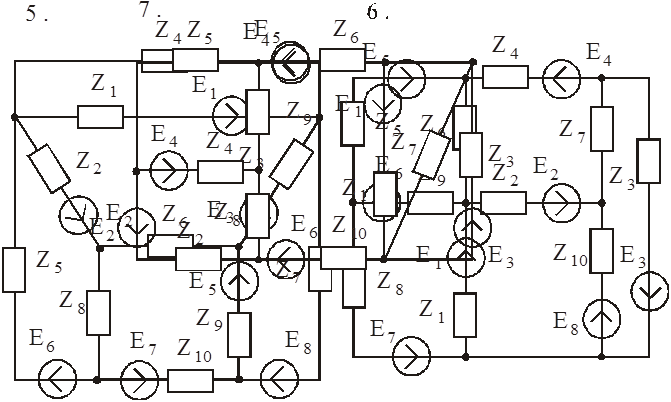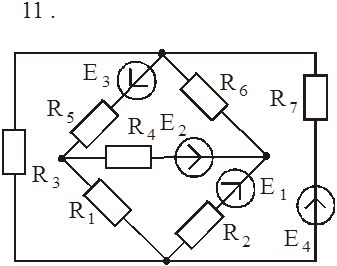Задача 4.
В схеме (рис. 23) определить показания приборов, если сопротивления амперметров считать равными нулю, а сопротивления вольтметров – бесконечно большими. Напряжение источника U=20 В.
 |
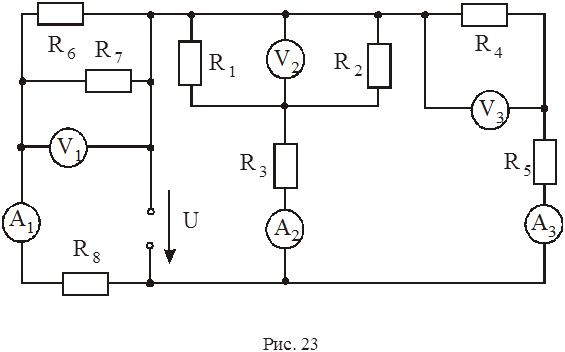Таблица 5
| Вариант | Данные к задаче 4 | |||||||
| R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | R7, Ом | R8, Ом | |
| ¥ | ||||||||
| ∞ | ||||||||
| ∞ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ¥ | |||||||
| ¥ | 2,5 | |||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| 7,5 | ||||||||
| ¥ | ¥ | |||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
| ¥ | ||||||||
Задача 5.
В цепи (рис. 24) три источника питания, ЭДС которых равны Е 1, Е 2, Е 3; их внутренние сопротивления соответственно равны R01=0,1 Ом; R02=0,2 Ом; R03=0,3 Ом. Отдельные ветви цепи могут быть разомкнуты при помощи рубильников Р1, Р2, Р3, Р4, Р5, Р6. Сопротивления в пассивных ветвях R1=1,5 Ом; R2=2 Ом; R3=2,5 Ом; R4=2 Ом; R5=R6=R7=R8=3 Ом. Определить по методу непосредственного применения законов Кирхгофа токи во всех ветвях и режимы работы источников энергии. Составить баланс мощностей.
 |
Таблица 6
| Вариант | Данные к задаче 5 | |||
| Е1, В | Е2, В | Е3, В | Разомкнуты рубильники | |
| Р4, Р5, Р6 | ||||
| Р2, Р5, Р6 | ||||
| Р2, Р4, Р5 | ||||
| Р1, Р4, Р6 | ||||
| Р2, Р3, Р6 | ||||
| Р4, Р5, Р6 |
Продолжение табл. 6
| Вариант | Данные к задаче 5 | |||
| Е1, В | Е2, В | Е3, В | Разомкнуты рубильники | |
| Р2, Р4, Р5 | ||||
| Р2, Р3, Р6 | ||||
| Р1, Р4, Р6 | ||||
| Р2, Р5, Р6 |
СПИСОК ЛИТЕРАТУРЫ
1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М.: Энергоатомиздат, 1989. – 528 с.
2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. – М.: Высш. шк., 1996. – 638 с.
3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники.– М.: Энергия, 1981. Ч. 1. – 536 с.
4. Теоретические основы электротехники. / Под ред. П.А. Ионкина. – М.:
Высш. шк., 1976. Т. 1. – 544 с.
5. Атабеков Г.И. Теоретические основы электротехники. – М.: Энергия,
1978. Ч. 1. – 592 с.
Составители: О. П. Куракина, В. Л. Федоров
Редактор В. А. Маркалева
ЛР № 020321 от 28.11.96
Подписано в печать. Формат 60x84 1/16.
Оперативный способ печати. Усл. печ. л. 2.0. Уч..-изд. л. 2.0
Бумага офсетная. Тираж. Заказ.
Издательство ОмГТУ. 644050, Омск, Пр. Мира, 11
типография ОмГТУ
