1. Выбираем случайные большие простые числа P и Q. Для обеспечения максимальной безопасности P и Q выбирают примерно равной длины и хранят в секрете.
2. Вычисляем модуль 
. Формируем функцию Эйлера 
.
3. Открытый ключ ОКА выбирается случайно таким образом, чтобы выполнялись следующие условия:
1<ОКA<  , НОД(ОКА, )=1
| (7.1) |
4. Секретный ключ СКA находится по сформированному открытому ключу так, что
| СКА×ОКА (mod )º1
или
СКА=ОКА-1 (mod (P-1) × (Q-1))
| (7.2) |
Здесь функция mod - взятия остатка от деления. Пользователь A может легко сформировать СКА, используя расширенный алгоритм Евклида, зная числа P и Q, а значит и 
.
Любой другой пользователь не может, зная открытый ключ ОКА вычислить СКА, так как ему не известны числа P и Q. Для их нахождения ему потребуется факторизовать известное ему большое число N, что является вычислительно сложной задачей.
Шифрование и дешифрование сообщений в криптосистеме RSA
Для того, чтобы зашифровать открытое сообщение M, отправитель B должен возвести его в степень открытого ключа пользователя А по модулю N. То есть шифрование выполняется в соответствие с формулой:
| (7.3) |
Обращение данной функции, то есть определение значения M по известным значениям С, ОКА, N практически не осуществимо при больших N (
).
Однако знание секретного ключа СКА позволяет обратить данную функцию, то есть решить задачу дешифровки криптограммы C. Для дешифровки криптограммы С необходимо возвести ее в степень секретного ключа пользователя А по модулю N. Таким образом, дешифрование сообщения выполняется в соответствие с формулой:
| (7.4) |
Получатель А, который создает ключевую пару (ОКА,СКА) защищает два параметра:
· секретный ключ СКА.
· пару чисел P и Q.
Рассекречивание данных чисел приводит к тому, что злоумышленник сможет вычислить 
, а значит и вычислить секретный ключ СКА согласно (7.3).
Открытыми в криптосистеме RSA являются только значения ОКА и N.
Пример 7.1
Зашифруем сообщение DAC по алгоритму RSA. Для простоты вычислений будем оперировать с небольшими числами P и Q.
Действия получателя А
1. Выберем P = 5 и Q = 13
2. Найдем 
3. 
.
4. В качестве ОКА необходимо выбрать значение, удовлетворяющее условиям 
, 
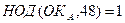. Пусть
ОКА = 5.
5. Необходимо найти СКА, такой что 
. Этому условию удовлетворяет число СКА =29,
определяемое подбором. Оно не единственно. Действительно, 
.
6. Отправляем пользователю B пару чисел по открытому каналу связи (N= 65, ОКА =5)
Действия отправителя B
1. Представим отправляемое сообщение в виде последовательности целых чисел от 0 до 63. Присвоим букве А
номер 1, букве B – 2, С – 3, D – 4 и т.д. Тогда открытый текст DAC запишется в виде последовательности чисел
413, то есть M1 =4, M2 =1, M3 =3.
2. Сформируем шифротекст по формуле (7.3):
, 
, 
.
2. B отправляет для A криптограмму { C1, C2, C3 }= {49, 1, 48}.
Действия пользователя A
1. Раскрываем шифротекст по формуле (7.4):
,
.
Таким образом, восстановлено исходное сообщение M1 =4=D, M2 =1=A, M3 =3=C. Исходное сообщение – DAC.
