ДВОЙСТВЕННЫЕ ЗАДАЧИ
Постановка задачи
Каждой ЗЛП определенным образом ставится в соответствие другая ЗЛП, называемая двойственной по отношению к исходной.
Исходная и двойственная задачи образуют единую пару двойственных задач.
Часто бывает так, что ЗЛП в исходной формулировке сложна для решения, – проще перейти к двойственной задаче, решить её и затем пересчитать и исследовать решение исходной задачи.
Симметричные двойственные задачи
Исходная задача в стандартной форме:
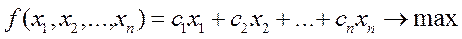(1)
при условиях связи: 
(2)
(3)
Правила построения двойственной задачи.
1. Каждому неравенству системы связей (2) ставим в соответствие переменную 
:
.
2. Составляем линейную целевую функцию переменных , коэффициентами которой являются свободные члены системы (2) и ищем её минимум:
. (4)
3. Составляем систему ограничений с матрицей, транспонированной к исходной матрице;
знаки неравенств меняем на противоположные;
свободными членами, равными коэффициентами исходной целевой функции:
. (5)
4. Вводим условие неотрицательности введенных переменных :
(6)
Кратко:
Исходная:
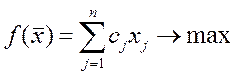
| Двойственная:
|
Замечание.
Если к двойственной задаче снова построить двойственную, то получим исходную задачу.
Прямая и двойственная задача называются симметричными взаимодвойственными задачами.
Пример 1. Построить двойственную задачу к исходной ЗЛП.
Исходная:
| Двойственная: |
Составим двойственную задачу.
1.
Исходная:
| Двойственная: |
2.
| Исходная:
| Двойственная:
|
3.
| Исходная:
| Двойственная:
|
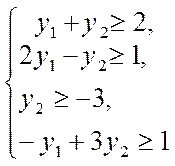
4.
| Исходная:
| Двойственная:
|
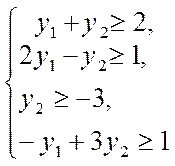
Несимметричные двойственные задачи
Исходная задача задана в канонической форме:
Исходная:
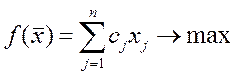
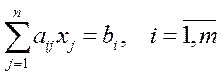
| Двойственная:
|
Исходная:
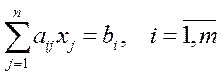
| Двойственная:
|
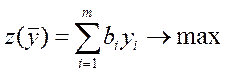
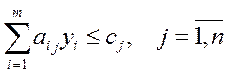
Замечание.
Для несимметричной двойственной задачи отсутствует условие неотрицательности 
.
Пример 2. Построить двойственную задачу к исходной ЗЛП.
Исходная:
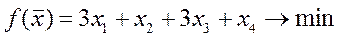
| Двойственная: |
Решение.
Исходная:
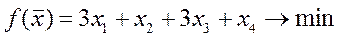
| Двойственная:
|
Смешанная двойственные задачи
Исходная задача задана в общем виде.
При составлении двойственной задачи руководствуемся правилами составления симметричных и несимметричных задач.
Пример 3. Построить двойственную задачу к исходной ЗЛП.
Исходная:
| Двойственная: |
Решение.
Исходная:
| Двойственная:
|
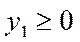
Основные теоремы двойственности
Теорема 1. (первая теорема двойственности)
Если одна из двойственных задач имеет оптимальное решение, то и другая его имеет, причем оптимальные значения целевых функций совпадают:
(7)
Если же в одной задаче целевая функция не ограничена, то двойственная ей задача не имеет допустимых решений.
Пример 4.
Исходная:
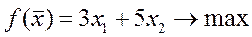
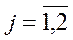
| Двойственная:
|
Теорема 2. (вторая теорема двойственности)
Для оптимальности допустимых решений 
и 
пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:
(8)
Исходная:
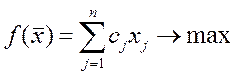
| Двойственная:
|
Теорема утверждает, что если в оптимальном решении одной из двойственных задач какая-либо переменная отлична от нуля, то соответствующее ей ограничение в другой задаче выполняется как строгое равенство.
Наоборот, если какое-либо ограничение выполняется как строгое неравенство, то соответствующая ему переменная в другой задаче равна нулю.
