Пример

Задача об использовании сырья
Для производства четырех видов изделий A1, A2, A3, A4 завод должен использовать три вида сырья I, II, III, запасы которого на планируемый период составляют соответственно 1000, 600 и 150 условных единиц. В приведенной ниже таблице даны технологические коэффициенты, т.е. расход каждого вида сырья на производство единицы каждого изделия и прибыль от реализации единицы изделия каждого вида.
| Виды сырья | Запасы сырья | Технологические коэффициенты | |||
| A1 | A2 | A3 | A4 | ||
| I | |||||
| II | |||||
| III | |||||
| Прибыль от реализации | 2,5 |
Требуется составить такой план выпуска указанных изделий, чтобы обеспечить максимальную прибыль от их реализации.
Составим математическую модель задачи
Обозначим через x1, x2, x3, x4 количество единиц соответствующих изделий: A1, A2, A3, A4. Тогда экономико-математическая модель задачи будет следующая: найти максимум функции
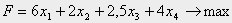
при выполнении системы ограничений

|
Для обращения системы ограничений-неравенств в систему уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные x5, x6, x7. Эти добавочные переменные в условиях данной задачи имеют конкретное экономическое содержание, а именно: объем остатков сырья каждого вида после выполнения плана выпуска продукции.

|
После введения добавочных переменных получим систему уравнений: Нужно найти такое допустимое базисное решение системы, которое бы максимизировало целевую функцию F, т.е. необходимо найти оптимальное решение задачи. Так как система ограничений состоит из трех независимых уравнений с семью переменными, то число основных (базисных) переменных должно равняться трем, а число неосновных — четырем.
Для решения задачи симплексным методом, прежде всего, нужно найти любое базисное решение. В условиях данной задачи оно может быть найдено без труда. Для этого достаточно принять за основные добавочные переменные x5, x6, x7. Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель (определитель единичной матрицы равен 1, т.е. отличен от нуля).
Положив неосновные (свободные) переменные x1, x2, x3, x4 равными нулю, получим базисное решение (0; 0; 0; 0; 1000; 600; 150), которое оказалось допустимым. Поэтому в условиях данной задачи отпадает надобность в применении первого этапа симплексного метода. Переходим сразу ко второму этапу, т.е. к поискам оптимального решения.
I шаг. Основные переменные x5, x6, x7. Составляем первую симплекс-таблицу. Находим разрешающий элемент.
| Базисные переменные | Свобод. члены | x5 | x6 | x7 | x1 | x2 | x3 | x4 |
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| F | -6 | -2 | -2,5 | -4 |
Базисное решение (0; 0; 0; 0; 1000; 600; 150).

II шаг. Основные переменные x1,x5, x6. Составляем новую симплекс-таблицу. Снова находим разрешающий элемент.
| Базисные переменные | Свобод. члены | x5 | x6 | x7 | x1 | x2 | x3 | x4 |
| x5 | -5 | -10 | -3 | |||||
| x6 | -4 | -6 | -3 | |||||
| x1 | ||||||||
| F | -2 | 9,5 |
Базисное решение (150; 0; 0; 0; 250; 0; 0).

III шаг. Основные переменные x1, x2, x5. Составляем новую симплекс-таблицу. Находим разрешающий элемент.
| Базисные переменные | Свобод. члены | x5 | x6 | x7 | x1 | x2 | x3 | x4 |
| x5 | -0,5 | -3 | -7 | -1,5 | ||||
| x2 | 0,5 | -2 | -3 | -1,5 | ||||
| x1 | ||||||||
| F | 3,5 | -1 |
Базисное решение (150; 0; 0; 0; 250; 0; 0).

IV шаг. Основные переменные х2, х4, х5. Переходим к следующей таблице.
| Базисные переменные | Свобод. члены | x5 | x6 | x7 | x1 | x2 | x3 | x4 |
| x5 | -0,5 | -1,5 | 1,5 | -4 | ||||
| x2 | 0,5 | -0,5 | 1,5 | |||||
| x4 | ||||||||
| F | 5,5 |
Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (0; 225; 0; 150; 475; 0; 0) при котором Fmax =1050, т.е. для получения наибольшей прибыли, равной 1050 денежных единиц, предприятие должно выпустить 225 единиц продукции вида A2, 150 единиц продукции вида A4, (продукцию вида A1 и A3 в данных условиях производить не выгодно) при этом сырье типа II и III будет использовано полностью, а 475 единиц сырья типа I останутся неизрасходованными.
http://matmetod-popova.narod.ru/theme24.htm






