Объем правильно восстановленной информации определяется следующим образом:
Назовем задачу чувствительной к возмущающим воздействиям (погрешностям исходных данных), если даже малые возмущающие воздействия (малые погрешности исходных данных) могут привести к значительной погрешности результата, и нечувствительной в противном случае. Значительная чувствительность к возмущениям лишает даже потенциальной возможности получения результата решения задачи с малой погрешностью. В силу этого чрезвычайно важной и актуальной является численная оценка такой чувствительности, установления параметров, определяющих чувствительность, достаточных условий нечувствительности задачи.
Если задача является чувствительной к возмущающим воздействиям, то даже незначительные изменения исходных данных (малые возмущающие воздействия) сильно изменят результат ее решения. Если же задача нечувствительна, то малые «сбои» исходных данных на самом объекте не отразятся. Пусть 
― входные данные для некоторой задачи, результатом решения которой является 
; 
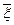― возмущенные входные данные, а решение задачи, полученное для этих входных данных, ― 
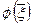. Числом обусловленности задачи называется величина, определяемая соотношением [69,70]:
. (1)
Расстояния, фигурирующие в формуле (1), определяются введением соответствующих метрик в пространствах входных данных и результатов. Необходимо отметить, что по смыслу соотношение (1) представляет из себя некий аналог абсолютного значения скорости изменения вещественной функции результата в точке .
Очевидно, чем меньше число обусловленности, тем меньше возмущение результата зависит от возмущения входных данных, тем меньше чувствительность задачи, а при малом числе обусловленности задача окажется нечувствительной к погрешностям исходных данных. Таким образом, число обусловленности задачи является ее мерой чувствительности к возмущающим воздействиям.
Одно из основных требований, выдвигаемых к любому СС с целью обеспечения эффективного декодирования секретной информации, — требование его нечувствительности к возмущающим воздействиям.
В общем случае чувствительность объекта определяется чувствительностью задачи о его формировании. Возмущающие воздействия, которым подвергается уже сформированное СС в ходе его транспортировки или хранения, — атаки, могут рассматриваться как дополнительные возмущения при его формировании. Чувствительность СС — это чувствительности задачи его получения. Если задача чувствительна, то даже малые возмущающие воздействия могут привести к значительным возмущениям результата — СС, что, в свою очередь, повлечет снижение эффективности декодирования секретной информации.
Определение 1. СС будем называть чувствительным, если даже незначительные возмущающие воздействия, которым оно подвергается, способны разрушить значительную часть погруженной ДИ и привести к большому росту количества ошибок при декодировании ДИ, и нечувствительным в противном случае.
1. Способ пересылки и декодирования дополнительной информации
Пусть 
— 
-матрица контейнера, 
, а в качестве ДИ выступает случайно сформированная бинарная числовая последовательность, содержащая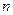 
элементов из множества 
, рассматриваемая ниже как вектор 
длины 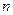. Последовательность может содержать менее 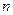элементов, тогда она дополняется незначащими элементами до нужной длины.
Основные шаги метода двухэтапного декодирования ДИ SYSTEMA следующие:
- Погружение ДИ.
а) Вычислить произведение
.
В предположении отсутствия ошибок округления, вектор является
точным решением СЛАУ
.
б) Вектор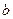 
погрузить в вместо вектора ДИ каким- либо СМ (СМ1).
- Декодирование.
а) Из полученого СС, возможно подвергшегося возмущениям при пересылке, извлечь погруженный вектор 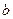в возмущенном виде 
при помощи СМ1. После извлечения вектора матрица изображения 
, в общем случае, будет отлична от .
б) Извлечь путем решения неоднородной СЛАУ
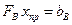, (2)
где 
;
— возмущения матрицы системы и вектора правой части 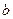соответственно;
— результат декодирования в условиях возмущенных входных данных.
Использование предлагаемого способа пересылки и декодирования ДИ SYSTEMA, включающего дополнительный этап в виде решения СЛАУ, при обеспечении достаточного условия устойчивости метода, обоснованного ниже, дает возможность увеличить объем 
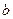правильно восстановленной информации по сравнению с непосредственной пересылкой на месте вектора при абсолютно аналогичных условиях.
- Условие устойчивости метода SYSTEMA
Пусть 
, где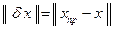 
— абсолютная погрешность 
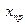. Тогда СЛАУ (2) представляется в виде:
(3)
Учитывая, что и , выразим из (3) 
:
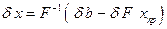, (4)
откуда, принимая во внимание элементарные свойства нормы и невырожденность матрицы , получаем:
(5)
Выбор конкретных матричной и векторной норм не существенен, поэтому никак не оговаривается. Важно лишь, что эти нормы согласованные.
Поскольку 
, разделив неравенство (5) на 
, получим:
. (6)
Из (6) вытекает, что 
является числом обусловленности, а значит мерой чувствительности задачи о решении СЛАУ к погрешности в исходных данных. Если число обусловленности матрицы ЦИ-контейнера мало, задача декодирования ДИ на втором этапе SYSTEMA является нечувствительной, малые возмущения на входе незначительно изменят результат, 
.
Предположим, что значения
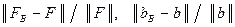(7)
невелики. Соотношения (7) анализируют возмущения всей матрицы и всего вектора в целом. Даже большая погрешность, возникающая в отдельных пикселях СС при небольшом их количестве не отразится значительно на оценках для выражений (7), а, значит, при хорошей обусловленности матрицы , и на значениях элементов вектора в силу (6), хотя некоторые элементы 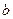могут быть сильно «испорчены». Подтверждением этого являются результаты вычислительного эксперимента, приведенные ниже.
Основным вычислительным звеном SYSTEMA является решение СЛАУ (2). Применение устойчивого численного метода к произвольной неоднородной системе с невырожденной матрицей в общем случае не гарантирует получение результата с малой погрешностью. Даже если вектор невязки, определяемый как
, (8)
мал, это не означает, что . Действительно, из (8) получаем, что 
, и соответственно
, (9)
откуда 
. Очевидно, что малость (8) гарантирует малую относительную погрешность решения только в том случае, когда матрица системы хорошо обусловлена.
Таким образом, для эффективного использования метода SYSTEMA в качестве контейнера нужно использовать ЦИ, с хорошо обусловленной матрицей.
Величина 
— число обусловленности Скила — также, как и 
, позволяет оценить относительную погрешность результата, где 
— матрица, составленная из модулей элементов .
Имеет место следующая теорема.
Теорема 1. Пусть матрица изображения, используемого в качестве контейнера, имеет малое число обусловленности Скила. Тогда метод SYSTEMA является устойчивым.
- Способ обеспечения малого числа обусловленности Скила матрицы произвольного изображения
Оценка числа обусловленности Скила для матрицы контейнера является ключевым моментом в вопросе выбора подходящего для пересылки ДИ методом SYSTEMA контейнера. Непосредственное вычисление числа обусловленности Скила для матриц большой размерности — процесс дорогостоящий. Кроме того, если контейнер является навязанным, его матрица плохо обусловлена, это, на первый взгляд, вообще лишает возможности использование метода SYSTEMA для обеспечения дополнительной защиты секретной информации.
Предлагается способ, позволяющий использовать практически любое изображение в качестве контейнера в методе SYSTEMA, независимо от его реального числа обусловленности.
Для диагональной матрицы 
, а значит SYSTEMA будет устойчив. Аналогичную картину можно ожидать и в случае, когда для элементов выполняется условие:
(15)
Но реальные изображения редко удовлетворяют свойству (15). Обеспечим малость числа обусловленности Скила матрицы изображения, не изменяя ее явно, а лишь моделируя виртуально значительное диагональное преобладание.
Пусть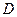 
— диагональная матрица размером 
с элементами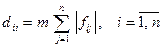 
, где 
, — элементы матрицы исходного изображения, 
— параметр. Выбор 
обеспечивает для 
наличие свойств, близких к (15), но поскольку 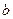для используемой СЛАУ вычисляется в соответствии с выражением 
, то значение не может быть произвольно большим.
Реально матрица не меняется, а виртуально построенная для нее матрица очевидно имеет диагональное преобладание. При получении СС, для которого контейнер — матрица , на втором этапе декодирования в SYSTEMA решается СЛАУ
, (16)
где 
— диагональная матрица, которая формируется декодером по полученной возмущенной матрице с элементами 
: 
, 
.
Поскольку свойства матрицы системы (16) близки к свойствам (15), решение СЛАУ (16) 
мало. Таким образом, практический метод введения виртуальной диагонали в матрицу реального изображения обеспечивает хорошую обусловленность Скила матрицы СЛАУ для декодирования ДИ и устойчивость SYSTEMA практически для любого ОС в предположении устойчивости алгоритма СМ1 декодирования b.
