Построение эпюр скоростей для сечения в месте установки скоростной трубки и т.д.

 

Анализируя схему циркуляционной установки можно сделать вывод, что расход жидкости постоянный в любом сечении трубопровода. Следовательно, режим течения жидкости зависит от диаметра трубопровода на рассматриваемом участке. Это, в свою очередь, говорит об идентичности режима течения на участках трубопровода с одинаковыми диаметрами. В месте установки скоростной трубки режим течения идентичен режиму течения на участке трубопровода всасывающей линии. Следовательно, мы имеем турбулентный режим течения, который происходит в зоне сопротивления шероховатых труб.

Формула для распределения скоростей в круглой трубе при турбулентном режиме в зоне шероховатых труб имеет следующий вид:

 

(23)

 

где U – местная скорость в данной точке сечения;

U٭ – динамическая скорость;

– диаметр трубопровода;

y – расстояние от оси трубопровода до рассматриваемой точки;

∆ – эквивалентная шероховатость стенок труб;

 

(24)

 

где 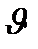– средняя скорость течения жидкости;

λ – коэффициент гидравлического сопротивления;

 

(25)

 

где h – показание дифманометра (или дифпьезометра) скоростной трубки. Подставив (24) и (25) в (23) получим:

 

(26)

 

 

где h – показание дифманометра скоростной трубки.

 

Аналогично по (26) для других значений y расчетные значения U приведены в табл. 2, а по ее данным построен рис. 3.

 

Таблица 2 – Расчетные значения скорости U по сечению трубопровода

y, м		0,01	0,02	0,03	0,04	0,05	0,055
U, м/c	1,01	0,99	0,97	0,93	0,88	0,77	0,36

 

 

Рис. 3 – Эпюра скоростей во всасывающем трубопроводе d₁=110 мм при расходе Q=0,0067 м³/c

 

4.4 Определение установившегося уровня жидкости в промежуточной ёмкости C

Для определения установившегося уровня жидкости в промежуточной ёмкости составим уравнение Бернулли для сечений 1–1 и 2–2 (рис.4):

 

(27)

 

где – расстояние от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

р – давления в сечениях А-А и В-В соответственно (Па);

– плотность циркулирующей жидкости (кг/м³);

g – ускорение свободного падения g = 9,81 м/ ;

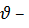скорость течения жидкости в сечении 1–1 и 2–2 соответственно (м/с);

коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях 1–1 и 2–2 соответственно. потери напора на участках между выбранными сечениями. Плоскость сравнения совместим с сечением 2-2, тогда . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора , (для практических расчетов).Т. к. диаметр промежуточной ёмкости во многом больше диаметра насадки значит .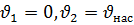

, т.к емкость открытая. Запишем уравнение Бернулли (31) с учётом всех утверждений:

(28)

Рисунок 4 – К определению уровня в промежуточной емкости С

 

Зная расход можно определить :

 

(29)

 

Подставляя (33) в (32) получим:

 

(30)

 

В действительности при прохождении жидкости через насадок в нем возникают потери напора, учтём их с помощью коэффициента расхода

, подставив его в формулу (34) получим:

 

(31)

 

Для цилиндрического внешнего насадка коэффициент расхода

. Тогда для нашего случая при получим:

 

(32)

 

4.5 Определение разности показаний манометров Р_м2 и Р_м3

Для сечений Р_м2 и Р_м3 уравнение Бернулли имеет вид:

 

(33)

 

где 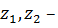расстояние от сечений Р_м2 и Р_м3 соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

– давления в сечениях Р_м2 и Р_м3 соответственно (Па);

– плотность циркулирующей жидкости (кг/м³);

g – ускорение свободного падения (м/с²);

скорость течения жидкости в сечении Р_м2 и Р_м3 соответственно (м/с);

коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях Р_м2 и Р_м3 соответственно.

потери напора на участках между выбранными сечениями.

 

Рисунок 5 – Манометры Р_м2 и Р_м3

Выберем ось трубопровода за начало отсчета, тогда , т.к трубопровод горизонтален. 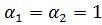, (для практических расчетов).

Потери напора между выбранными сечениями определяются только потерями напора по длине трубопровода, т.к местных сопротивлений на данном участке нет; , т.к расход и площадь поперечного сечения одинаковы для сечений Р_м2 и Р_м3. В итоге формула (37) примет вид:

 

; ; (34)

 

Потери напора по длине трубопровода определяются по формуле Дарси-Вейсбаха:

(35)

 

Подставим (35) в (34):

(36)

(37)

 

Подставив в (37) значения параметров получим при

 

=820 0,029 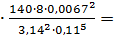7530 Па=7,53 кПа