Внимание!
Подставьте при необходимости значение переменной n в примеры Вашего варианта.
n -номер студента в списке группы.
Вопросы к ЗАЧЕТУ
1. Определение предела функции в точке. Бесконечно большие, бесконечно малые и ограниченные функции.
2. Понятие предела функции. Бесконечно малые и бесконечно большие функции: определение, сравнение, взаимосвязь. Теоремы о бесконечно малых и бесконечно больших функциях.
3. Основные теоремы о пределах.
4. I замечательный предел. Сравнение бесконечно малых функций. II замечательный предел.
5. Непрерывность функций в точке и на интервале. Точки разрыва.
6. Основные теоремы о непрерывных функциях.
7. Определение производной функции 1 переменной; её геометрический смысл. Дифференцируемость функции в точке и на интервале. Правила дифференцирования.
8. Определение производной функции 1 переменной. Дифференцирование обратных, сложных и параметрически заданных функций.
9. Определение производной и дифференциала функции 1 переменной. Производные и дифференциалы высших порядков.
10. Определение производной функции 1 переменной. Теорема Ролля и ее геометрический смысл. Теорема Лагранжа и ее геометрический смысл.
11. Правило Лопиталя для раскрытия неопределённостей  и
и 
12. Монотонность функции 1 переменной. Необходимые и достаточные условия возрастания и убывания.
13. Монотонность функции 1 переменной. Точки экстремума. Необходимое условие экстремума, его геометрический смысл. Критические точки.
14. Точки экстремума. I и II достаточное условия экстремума. Алгоритм исследования функции на экстремум.
15. Выпуклость и вогнутость графика функции. Точки перегиба. Достаточное условие точки перегиба.
16. Асимптоты графика функции: вертикальные и наклонные.
17. Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла.
18. Неопределенный интеграл. Подведение под знак дифференциала и правило масштабирования.
19. Неопределенный интеграл. Замена переменных. Интегрирование по частям.
20. Интегрирование дробно-рациональных функций. Интегрирование простейших дробей 4-х типов. Разложение дроби на сумму простейших дробей 4-х типов.
21. Интегрирование тригонометрических функций и иррациональных выражений.
22. Определенный интеграл. Определение. Геометрический смысл. Основные свойства. Формула Ньютона – Лейбница.
23. Замена переменной и интегрирование по частям в определенном интеграле.
24. Геометрические приложения определенного интеграла: вычисление площади плоской фигуры.
25. Геометрические приложения определенного интеграла: вычисление длины дуги плоской кривой и объёмов тел вращения.
26. Несобственные интегралы I и II рода; их сходимость и расходимость.
27. Приближенное вычисление определенных интегралов.
28. Применение дифференциального и интегрального исчисления к решению экономических задач.
Задача. Изобразить эскиз графика и описать по общей схеме функцию
| № п/п | Функция | № п/п | Функция |

| 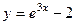
| ||
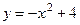
| 
| ||

| 
| ||

| 
| ||
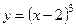
| 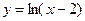
| ||
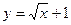
| 
| ||

| 
| ||

| 
| ||
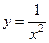
| 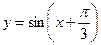
| ||
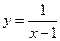
| 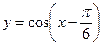
| ||
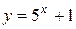
| 
| ||
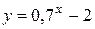
| 
| ||

| 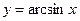
| ||
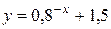
| 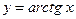
|
Основная литература:
- Высшая математика для экономистов. Под редакцией проф. Н.Ш. Кремера. М., Юнити, 2006, 2010.
- Демидович Б.П. Краткий курс высшей математики: уч. пособие для вузов / Б.П. Демидович, В.А. Кудрявцев. – М.: АСТ, 2007. – 654 с.
- Общий курс высшей математики для экономистов: Учебник / Под общ. ред. В.И. Ермакова. - М.: ИНФРА-М, 2008. – 656 с.
Министерство образования и науки российской федерации
Тульский филиал
федерального государственного бюджетного образовательного учреждения
высшего образования
«Российский экономический университет им. Г.В. Плеханова»
(Тульский филиал РЭУ им. Г.В. Плеханова)






