ДА min = ПР да /О да
ДА min = ДА к + (ПР да - ФР да)/О да
Диапазон колебаний остатка денежных активов в предстоящем периоде исходя из плана поступления и расходования денежных средств
| месяцы | Остаток денежных активов на конец месяца, млн. руб. | Отклонение месячного показателя от среднего, млн. руб. (+/-) | Отклонение месячного показателя от среднего, % (+/-) | Отклонение месячного показателя от минимального, млн. руб. | Отклонение месячного показателя от минимального, % |
| 1,30 | -0.16 | -10.9 | 0.05 | 4.0 | |
| 1,25 мин | -0.21 | -14.4 | |||
| 1,34 | -0.12 | -8.2 | 0.09 | 7.2 | |
| 1,42 | -0.04 | -2.7 | 0.17 | 13.6 | |
| 1,51 | 0.05 | 3.4 | 0.26 | 20.8 | |
| 1,48 | 0.02 | 1.4 | 0.23 | 18.4 | |
| 1,44 | -0.02 | -1.4 | 0.19 | 15.2 | |
| 1,52 | 0.06 | 4.1 | 0.27 | 21.6 | |
| 1,54 | 0.08 | 5.5 | 0.29 | 23.2 | |
| 1,56 | 0.10 | 6.8 | 0.31 | 24.8 | |
| 1,53 | 0.07 | 4.8 | 0.28 | 22.4 | |
| 1,58 max | 0.12 | 8.2 | 0.33 | 26.4 | |
| В среднем | 1.46 | ||||
Основной задачей любого финансового менеджера является максимально-точный прогноз объемов будущих запасов денежных средств, которые смогут обеспечить плановые темпы роста фирмы и ее способность своевременно погашать порожденные этим ростом обязательства. Исторически методами, используемыми для решения этой задачи, являются метод прогнозируемых пропорций, метод скорректированной доходности, модель Баумоля и модель Миллера-Орра.
Метод прогнозируемых пропорций заключается в том, что компания должна держать определенный процент от продаж в виде денежных средств. Стандартом часто служит отраслевое среднее. Весьма часто рассматриваемая модель является «неточной», так как не учитывает ни экономию на масштабах, ни возможные проблемы и/или задержки с платежами или с поступлением денег. Этот метод также не позволяет найти наилучшее значение кассового остатка.
Метод скорректированной доходности представляет собой «точку нулевого кассового остатка» и характеризует такой объем продаж, при котором совокупный приток денежных средств равен совокупному оттоку. Метод зависит от прогнозируемого отчета о прибылях и убытках и бухгалтерского баланса. Исходя из прогноза продаж, прибылей, источников и использования ресурсов, путем простых подсчетов возможно оценить, какой кассовый остаток потребуется предприятию в ближайшее время.
К сожалению, оба рассмотренных метода не учитывают стоимости хранения денежных средств. Этот недостаток отсутствует в моделях Баумоля, Миллера-Орра, Стоуна и в модели имитационного моделирования Монте-Карло. Рассмотрим основные положения данных моделей.
С помощью модели Баумоля можно определить оптимальное количество денежных средств для компании, которое следует хранить в условиях определенности. Модель Баумоля существенным образом опирается на условие, что альтернативой хранения денег является использование рыночных ценных бумаг и/или процентных депозитов.
Модель Баумоля основана на следующих предпосылках:
- спрос на денежные средства в каждом периоде известен и равен «D» денежных единиц;
- денежный остаток используется равномерно;
- все требования к оплате выполняются немедленно;
- стоимость затрат на конвертацию по превращению активов в деньги равна «с» денежных единиц и неизменна;
- альтернативная стоимость денег «v» равна упущенному проценту по облигациям за период.
В этих условиях, оптимальный остаток денежных средств определяется по формуле:
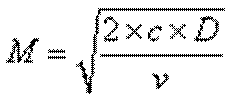
Модель Баумоля проста и приемлема для предприятий, денежные расходы которых стабильны и прогнозируемы. В действительности такое случается редко; остаток средств на расчетном счете изменяется случайным образом, причем возможны значительные колебания.
Модель Миллера - Орра
Модель, разработанная М. Миллером и Д. Орром, представляет собой компромисс между простотой и повседневной реальностью. Она помогает ответить на вопрос, как предприятию следует управлять своим денежным запасом, если невозможно с точностью предсказать каждодневный отток или приток денежных средств. Миллер и Орр использовали при построении модели процесс Бернул-ли — стохастический процесс, в котором поступление и расходование денег от периода к периоду являются независимыми случайными событиями.
|
| Рис. Модель Миллера — Орра |
Остаток средств на счете хаотически меняется до тех пор, пока не достигает верхнего предела. Как только это происходит, предприятие начинает скупать высоколиквидные ценные бумаги с целью вернуть запас денежных средств к некоторому уровню (точке возврата).
Если запас денежных средств достигает нижнего предела, то предприятие продает накопленные ранее ценные бумаги, пополняя запас денежных средств до нормального уровня.
При решении вопроса о размахе вариации (разность верхнего и нижнего пределов) рекомендуется придерживаться правила: если ежедневная изменчивость денежных потоков велика или постоянные затраты, связанные с покупкой и продажей ценных бумаг, высоки, то предприятию следует увеличить размах вариации, и наоборот. Также рекомендуется уменьшить размах вариации, если есть возможность получения дохода благодаря высокой процентной ставке по ценным бумагам.
Реализация модели осуществляется в несколько этапов.
1. Устанавливают минимальную величину денежных средств (Сmin). которую целесообразно постоянно иметь на расчетном счете. Она определяется экспертным путем исходя из средней потребности предприятия в оплате счетов, возможных требований банка, кредиторов и др.
2. По статистическим данным определяют вариацию ежедневного поступления средств на расчетный счет (Var) Предполагается также, что чистые денежные потоки колеблются с ежедневной дисперсией, равной.
3. Определяют расходы (v) по хранению средств на расчетном счете (обычно их принимают в сумме ставки ежедневного дохода по краткосрочным ценным бумагам, циркулирующим на рынке) и расходы (c) по взаимной трансформации денежных средств и ценных бумаг. Эта величина предполагается постоянной; аналогом такого вида расходов, имеющим место в отечественной практике, являются, например, комиссионные, уплачиваемые в пунктах обмена валюты.
4. Рассчитывают размах вариации остатка денежных средств на расчетном счете (R) по формуле
5. Рассчитывают верхнюю границу денежных средств на расчетном счете (Сmax), при превышении которой необходимо часть денежных средств конвертировать в краткосрочные ценные бумаги.
Cmax= Cmin+R
6. Определяют точку возврата (Сr) — величину остатка денежных средств на расчетном счете, к которой необходимо вернуться в случае, если фактический остаток средств на расчетном счете выходит за границы интервала
(Cmax, Cmin)
Пример
Приведены следующие данные, необходимые для оптимизации остатка денежных средств компании: минимальный запас денежных средств (Сmin) — 10 тыс. долл.; расходы по конвертации ценных бумаг (c) — 25 долл.; процентная ставка r= 11,6% в год; среднее квадратическое отклонение в день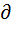 
— 2000 долл. С помощью модели Миллера — Орра определить политику управления средствами на расчетном счете.
Решение
1. Расчет показателя v
(1+r) = 1+0.116 = 1,116
отсюда: v = 0,0003, или 0,03% в день.
| 2. Расчет вариации ежедневного денежного потока Var = 20002 = 4000000. 3. Расчет размаха вариации (R). |
|
4. Расчет верхней границы денежных средств и точки возврата.
Сmax = 10000+ 18900 = 28900 долл.
Сr = 10000+1/3*18900 = 16300 долл.
Остаток средств на расчетном счете должен варьировать в интервале (10000, 28900); при выходе за пределы интервала необходимо восстановить средства на расчетном счете в размере 16 300 долл.
Эффективность использования оборотных активов может быть определена путем расчета продолжительности финансового цикла. Финансовый цикл – цикл обращения денежной наличности, в течение которого денежные средства отвлечены из оборота (с момента оплаты сырья и материалов, идущих в производство, до момента оплаты реализованной продукции, включая период дебиторской задолженности). Операционный цикл длиннее финансового на период погашения кредиторской задолженности.
Продолжительность финансового цикла может быть определена по формуле:
ПФЦ = ВОЗ + ВОД – ВОК, где
ВОЗ – время обращения производственных запасов
ВОД – время обращения дебиторской задолженности
ВОК – время обращения кредиторской задолженности
