Таблица 2
| Вариант | Тип задания | Поправка n |
| 1 – 10 | n = N | |
| 11 – 20 | n = N - 10 | |
| 21 – 30 | n = N – 20 | |
| 31 – 40 | n = N – 30 |
Например, для варианта 26 выбираются задачи третьего типа, а величина поправки равна 6.
 Указаниядлявведения исправлений в зависимости от поправки приводятся в условиях всех заданий.
Указаниядлявведения исправлений в зависимости от поправки приводятся в условиях всех заданий.
* За основу взят сборник заданий по геометрии недр (авт.: Базанов Г.А., Васильева Э.А.)
Указания к выполнению заданий и требования
К оформлению отчета
При решении задач первых четырех заданий рекомендуется придерживаться следующих правил:
1. Задания выполняются на листе миллиметровой бумаги размера А4. Размер чертежа для одной задачи 10х10 см. На одну страницу А4, таким образом, помещается две задачи (рис. 1).
2. Каждая задача обозначается тремя числами, например: 2–IV–(12), то есть вторая задача четвертого задания, вариант двенадцатый.
3. На листах следует наносить рамку сплошной основной линией на расстоянии 25 мм от левой стороны (для подшивки в альбом) и на расстоянии
10 мм от остальных сторон.
4. Подробные условия задач и методы их решения приводятся в пояснительной записке, а на чертеже – только цифровые данные.
5. Проекции точек обозначаются малыми, а совмещенные положения точек – большими буквами.
6. Основные элементы решения выделяются цветной тушью.
7. Пояснения по выполнению заданий пишутся на белом листе формата А4 в альбомной ориентации. С левой стороны каждой страницы оставляется поле для подшивки.

Рис. 1. Схема оформления заданий
8. Титульный лист отчета выполняется тушью на плотном листе ватмана формата А4 в альбомной ориентации.
Задачи на проекции, применяемые
В геолого-маркшейдерском деле
Задание I
1. Даны две точки А (х, у, z +n) и В (х, у, z +n), принадлежащие одной прямой (табл. 3).
Требуется:
а) изобразить прямую на плане в масштабе 1:1000 в проекции с числовыми отметками;
б) проградуировать прямую через h,м аналитическим и графическим методами.
Таблица 3
| Тип задачи | XА | YА | ZА | XВ | YВ | ZВ | h, м |
2. Дана прямая СD координатами точки С (х, у, z), дирекционным углом aСD + n и углом падения d + n (табл. 4).
Требуется:
а) построить в масштабе 1:5000 проекцию этой прямой;
б) проградуировать прямую через h, м.
Таблица 4
|
3. Дана прямая, проходящая через точки А (х, у, z) и В (х, у, z - n). Исходные данные приведены в табл. 5.
Требуется:
а) изобразить прямую на плане в масштабе 1:1000;
б) определить угол наклона прямой АВ к плоскости проекции;
в) определить дирекционный угол направления (ВА);
г) определить истинное расстояние между точками А и В;
Таблица 5
|
д) найти проекцию и координаты точки С, находящейся на прямой АВ на расстоянии l+n м от точки А.
4. На плане в масштабе 1:1000 изобразить прямую А (х, у, z), В (х, у, z - n) и точку С (х, у, z - n). Исходные данные приведены в табл. 6.
Таблица 6
|
Требуется:
а) через точку С провести прямую, параллельную прямой АВ;
б) определить дирекционный угол и угол наклона прямой АВ.
Примеры решения задач
Задача 1 – I. Дано А (130, 125, 187), В (150, 168, 211), h = 5 м.
Решение. По заданным координатам X и Y наносим на план проекции точек А и В, которые соединяют прямой линией. Около проекций точек записываем высотные отметки (рис. 2).
Для градуирования прямой АВ графическим способом необходимо построить вертикальный разрез по этой прямой. Этот разрез может быть построен на отдельном чертеже или на плане способом совмещения. Для совмещения вертикальную плоскость, проходящую через прямую АВ, вращают относительно какого-либо горизонта до совмещения этой вертикальной плоскости с горизонтальной. При этом все точки перемещаются по направлениям, перпендикулярным оси поворота. За горизонт поворота удобней всего выбрать горизонт точки с меньшей отметкой, для данного примера – 187.
Точка В находится выше точки А (оси поворота) на 24 м. Откладывая это расстояние по перпендикуляру, восстановленному из проекции точки В, к проекции прямой АВ получаем совмещенное положение точки В. Совмещенное положение точки А совпадает с ее проекцией, соединив совмещенные точки, получаем совмещенное положение прямой АВ. Горизонт, кратный 5 м и ближайший к 187 будет 190, его совмещенное положение будет изображаться прямой линией, параллельной оси (проекции АВ), проходящей на расстоянии 3 м от нее. Далее через 5 м пойдут горизонты 195, 200 и т.д. до 210 м. Проектируя совмещенные положения точек 190, 195, …210 на проекцию, решаем задачу по градуированию прямой.
Заметим, что если совмещенное положение прямой строится только для градуирования, то вертикальный масштаб может быть любым. Если же необходимо определить угол наклона прямой, расстояние АВ и т.д., тогда вертикальный масштаб должен быть одинаков с горизонтальным.
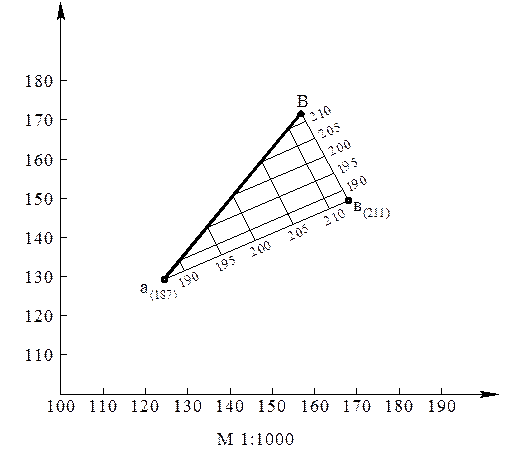
Рис. 2
Для того чтобы проградуировать прямую аналитическим способом, найдем заложение прямой при сечении h, составляя пропорцию:
 ,
,
где l АВ – заложение прямой АВ (длина проекции);
Н АВ – разность отметок точек А и В;
d – искомое заложение;
h – сечение градуирования.
Для данного примера (l АВ =48 м; Н АВ = 24 м; h = 5м) определяем заложение как
 м.
м.
Для нахождения на проекции точки 190 определяем заложение на 3 м  , которое откладываем на проекции от точки а. Остальные точки строим, откладывая заложение на 5 м.
, которое откладываем на проекции от точки а. Остальные точки строим, откладывая заложение на 5 м.
Задача 2 – I. Дано: С (320, 420, 215), aCD = 258 ○, d = 46 ○, h = 50 м.
Решение. Совмещенное положение прямой CD в этом случае строится не по высотным отметкам точек, а по углу наклона прямой. Направление прямой всегда указывается в сторону падения (если в сторону восстания, то это оговаривается особо) На рис. 3 из проекции точки С проведено направление CD. Откладывая от проекции угол наклона d, проводим совмещенное положение. Отметки горизонтов, кратные 50 м, будут меньше, чем горизонт поворота 215. Горизонт 200 проводим в 15 м от проекции прямой, остальные идут через 50 м. Далее переносим точки 200, 150, 100 и т.д. на проекцию.
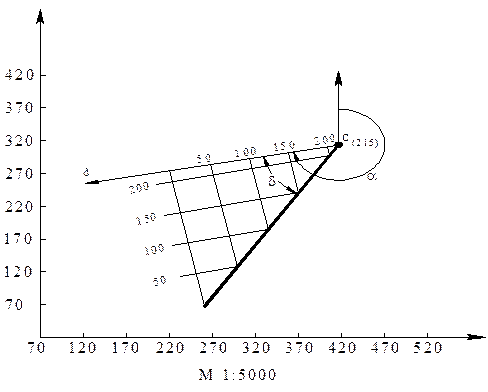
Рис. 3
Задача 3 – I. Решение этой задачи рассмотрим на примере задачи 1 – I.
Определение d = 26 ○, aВА = 245 ○ и расстояния АВ=55 м понятно из чертежа. Далее требуется найти проекцию и координаты точки С, находящейся на прямой АВ на расстоянии 25 м от точки А (рис. 4).
Откладывая это расстояние от точки А на совмещенном положении прямой, получаем совмещенное положение точки С, которую затем переносим на проекцию прямой. По осям X и Y снимаем соответствующие координаты (X = 139; Y = 145).
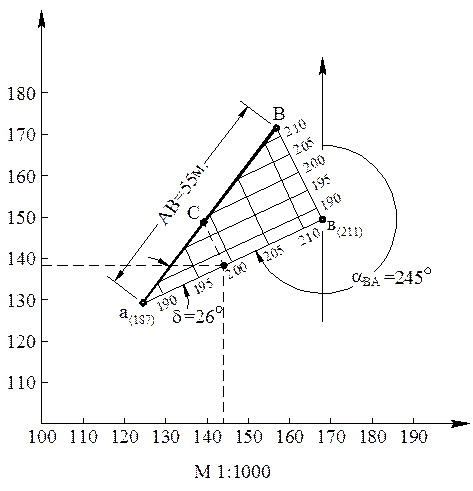
Рис. 4
Отрезок (С – с) является превышением точки С над горизонтом поворота (187), поэтому отметка точки С = 187 + (С – с) = 187 + 11 = 198 м.
Задача 4 – I. Дано: А (18, 32, 49), В (89, 56, 11), С (36, 82, 116).
Решение. Строим на плане проекцию прямой АВ. Через точку С проводим направление проекции параллельной прямой. Заложение для прямой АВ найдено, а заложение параллельной прямой должно быть таким же, причем отметки точек должны убывать в том же направлении, как и у прямой АВ.
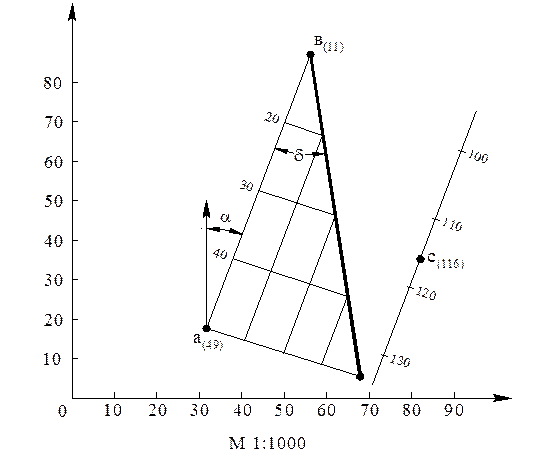
Рис. 5
Градуируем параллельную прямую, придерживаясь этих правил (рис. 5).
Задание II
1. Дана прямая с точками А (х, у, z), В (х, у, z), и точка С (х, у, z - n), не лежащая на этой прямой (табл. 7).
Требуется:
а) через прямую АВ и точку С провести плоскость, изобразив ее в горизонталях сечением через 10 м на плане в масштабе 1:1000;
б) определить дирекционный угол простирания плоскости и угол ее наклона.
Таблица 7
| Тип задачи | XА | YА | ZА | XВ | YВ | ZВ | XC | YC | ZC |
2. Даны две прямые, проходящие через точку А (х, у, z), из которых одна по направлению a1+2n и d1+n, другая – по направлению a2 и d2,
Требуется:
а) построить на плане плоскость;
б) определить элементы ее залегания (табл. 8).
Таблица 8
|
3. На плане в масштабе 1:2000 сечением горизонталей через 10 м изобразить плоскость по координатам трех точек: А (х, у, z), В (х, у, z), С(х, у, z). Исходные данные в табл. 9.
Требуется:
а) из точки D(х – 2n, у), лежащей на плоскости, восстановить перпендикуляр к плоскости длиной l + 2n, м;
б) определить координаты конца перпендикуляра и длину проекции перпендикуляра;
(табл. 10).
Таблица 9
|
с) определить угол наклона и дирекционный угол перпендикуляра (в сторону падения).
4. В точке А (х, у, z) измерены элементы залегания пласта aр+2n и dр+n
Требуется:
а) определить направление, угол наклона и длину проектной скважины, которая должна быть пробурена из точки С (х, у, z) перпендикулярно пласту;
б) найти координаты точки встречи скважины с пластом.
Таблица 10
|
Примеры решения задач
Задача 1 – II. Дано: А (138, 152, 49), В (209, 176, 11), С (156, 202, 35).
Решение. Строим проекции прямой АВ и точки С и градуируем прямую АВ через 10 м (рис. 6).
Через точку С и соответствующую ей отметку на прямой АВ проводим вспомогательную горизонталь плоскости. Параллельно этой горизонтали через отметки, кратные 10 м (20, 30 и т.д.), проводим остальные горизонтали плоскости. Направление простирания плоскости определяется по правилу: если встать лицом в сторону падения плоскости, то простирание будет влево. Дирекционный угол линии простирания определяется графически.
Угол наклона плоскости определятся через заложение. Для этого строится разрез вкрест простирания плоскости. Этот разрез может быть построен отдельно или на плане способом совмещения. Для данного примера aР = 280 ○,
dР = 28 ○.
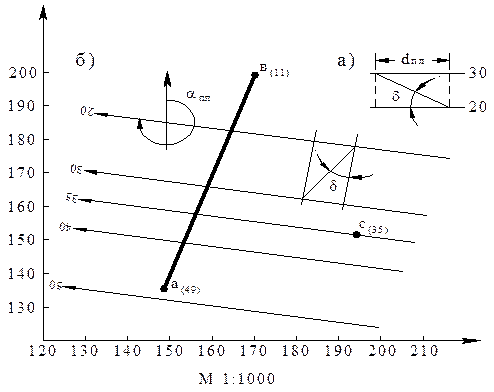
Рис. 6
Задача 2 - II. Дано: А (61, 55, 55), a1 = 120 ○, d1 = 30 ○, a2 = 250 ○, d2 = 25 ○.
Решение. Построив проекции прямых и проградуировав каждую, проводим горизонтали плоскости, соединяя точки с одинаковыми отметками (рис. 7). Дальнейшее решение ничем не отличается от предыдущего (задача 1 – II).

Рис. 7
Задача 3 – II. Дано: А (370, 90, 96), В (250, 230, 62), С (250, 370, 109), D (300, 300), l = 105 м.
Решение. Построим проекции точек А, В, С и, соединив их прямыми, получим проекцию треугольника, через который необходимо провести плоскость. Градуируем две стороны этого треугольника (у которых больше перепад высот) через 10 м и проводим горизонтали плоскости (рис. 8). Наносим на план точку D, которая находится на плоскости, и строим через нее разрез вкрест простирания плоскости (по линии наибольшего ската).
За ось поворота выбран горизонт точки D (88 м), эта точка при повороте остается на месте. Точка 1, имеющая отметку 100, при повороте сместится на 12 м по направлению, перпендикулярному оси поворота, в данном случае по горизонтали. Проводим через совмещенные положения точек D и 1 совмещенное положение плоскости. Восстанавливая из точки D перпендикуляр длиной 105 м, получаем его совмещенное положение. Проектируем далее совмещенное положение точки Е (конец перпендикуляра) на линию разреза и получаем проекцию перпендикуляра ed. Определение остальных элементов уже рассмотрено в предыдущих задачах.

Рис. 8
Задача 4 – II. Дано: А (185, 145, 190), aР =110 ○, dР = 30 ○, С (127, 120, 220).
Решение. Через точку А под дирекционным углом 110 ○ проводим горизонталь плоскости с отметкой 190. Принимая сечение горизонталей 10 м, определяем заложение плоскости графическим путем. Заложение может быть определено построением разреза отдельно или же на плане способом совмещения (рис. 9).
Из проекции точки С проводим направление перпендикуляра к плоскости и строим совмещенный разрез по этому направлению. Затем из совмещенного положения точки С проводим перпендикуляр к совмещенному положению плоскости. Точка К является совмещенным положением точки пересечения. Переносим ее на проекцию и определяем координаты этой точки. Длина линии С1 – К показывает длину скважины.
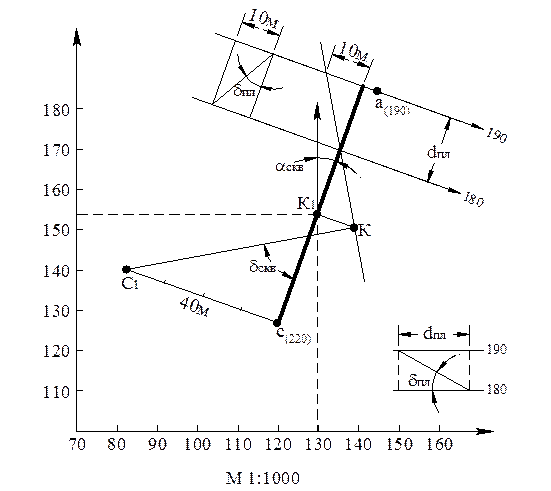
Рис. 9
Направление и угол наклона можно определить графическим путем, но так как нам известны элементы залегания пласта, то элементы залегания перпендикулярной скважины определяется aС =110 ○ – 90 ○ = 20 ○, d С = 90 ○ – 30 ○ = 60 ○.
Геометризация месторождений полезных ископаемых
Задание III
По результатам инклинометрической съемки скважины (табл. 11) требуется построить план скважины и проекцию ее на вертикальную плоскость разведочной линии. Дирекционный угол этой линии равен aЛ-n. Координаты устья скважины: ХС = 185 м, YС = 208 м, НС = 397 м.
В точке К, которая находится на расстоянии 15 м от точки 4, скважина встретила пласт угольной залежи.
Требуется определить:
1. Координаты точки встречи скважины с пластом (точка К);
2. Построить проекцию скважины на вертикальную плоскость разведочной линии.
Таблица 11
| Тип точки | |||||||||
| Точка замера | Глубина, м. | Зенит. угол Q° | Дирек-ционный угол a° | Зенит. угол Q° | Дирек-ционный угол a° | Зенит. угол Q° | Дирек-ционный угол a° | Зенит. угол Q° | Дирек-ционный угол a° |
| С | |||||||||
| aЛ° |
Решение:
1. По средним значениям зенитных углов для интервалов С-1, 1-2, и т.д. и длинам этих интервалов строится профиль по оси скважины (рис. 10, а; сплошная линия).
2. По средним значениям дирекционных углов интервалов и их горизонтальным проекциям (снимаемым с профиля) строится план скважины (рис. 19, б).
3. На плане через точку С проводитсянаправление плоскости разведочной линии, а затемна нее проектируются точки 1,2.....
4. Так как при проектировании точек на вертикальную плоскость высотные отметки точек остаются постоянными, то откладывая расстояния С-1', С-2 ', и т.д. на профиле на соответствующих уровнях от вертикали точки С, получаем проекции точек. Линия, соединяющая эти точки, является проекцией оси скважины на плоскость разведочной линии (рис. 19, а; пунктирная линия).
5. Плановые координаты точки К снимаются с плана, а высотная отметка с профиля (НК = НС - DНС-К).

Рис. 10.






