Постоянные и атмосферные нагрузки.

Постоянные нагрузки на ригель рамы обычно принимают равномер­но распределенными по длине ригеля (рис. а).

Величину расчетной постоянной нагрузки на 1 м² покрытия g_Kp удоб­но определять в табличной форме, в зависимости от конструкции кровли.

В распределенную поверхностную нагрузку включаются нагрузки от всех слоев кровли, конструкций фермы, фонаря, связей с соответствую­щими коэффициентами перегрузки. Линейная распределенная нагруз­ка на ригель собирается с площади A₁ (рис.1).

 

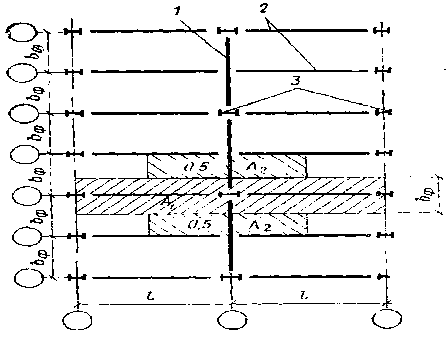
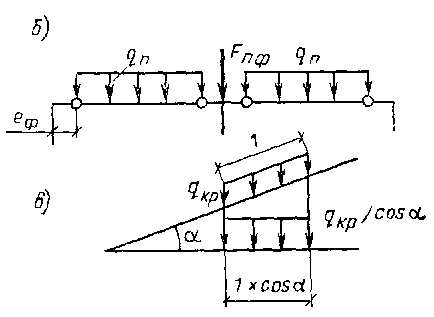
Рис. Расчетные схемы рам при расчете на постоянные нагрузки

1 — подстропильная ферма, 2 — стропильные фермы, 3 — колонны

При подсчете линейной нагрузки на ригель q_n(см. рис. а, б) нужно спроектировать q_KP на горизонтальную поверхность (см. рис.в) и собрать с ширины, равной шагу стропильных ферм b. Таким образом,

q_n = q_KP b /cos α

α – угол наклона верхнего пояса фермы. α<=250

то можно принять cos α=1;

Опорная реакция фермы

F_ПФ= q_n L/2

При шарнирном сопряжении ригеля с колонной нужно учесть внецентренность опирания фермы на колонну (см. рис. б), из-за которой возникает сосредоточенный момент, равный произведению опорной ре­акции фермы на эксцентриситет e.

M_Ф= F_ПФ e

При наличии подстропильных ферм на колонны передаются еще сосредоточенные силы F_ПФ, равные опор­ным реакциям подстропильных ферм.

Остальные постоянные нагрузки собирают в сосредоточенные силы, условно приложенные к низу подкрановой и надкрановой части колон­ны по оси сечения. Сила F₁ включает в себя собственный вес нижней части колонны и нагрузку от стен и остекления на участке от низа рамы до уступа колонны (если стена не самонесущая); аналогично сила F₂ включаете себя вес верхней части колонны и вес подвесных стен и остекления выше уступа F_П; си­лы F_1С и F_2С равны весу нижней и верхней частей средней колонны. Т.к. силы F_П и F_2С приложены с эксцентриситетом относительно оси нижней части колонны, то на уровне уступа возникает момент Mп

Mп= F_П(δ/2+ b +L)+(F_ПФ+ F_2С)e

Снеговая нагрузка. Нормативное значение снегового покрова P₀ на 1 м² горизонтальной поверхности земли определяется по данным гидромилиаративной службы и есть среднее значение веса снегового покрова за 10 лет наблюдений. Значения даны в СНиПе 2.01.07-85 нагрузки и воздействия в зависимости от района строительства. Нормативное значение на 1 м² покрытия определяется

P_Н=μ P₀

Эта нагрузка считается равномерно распределенной по длине ригеля. Расчётная линейная нагрузка.

q_СН = nμр₀ b, (12.9)

где р₀ — вес снегового покрова на земле, зависящий от района строительства и опре­деляемый по СНиП; μ — коэффициент перехода от нагрузки на земле к нагрузке на 1 м² проекции кровли, равный при уклоне а<25° единице; b —шаг ферм; n— коэф­фициент перегрузки равен 1,4.

Опорная реакция фермы

F_ПФ2= q_СН L/2

Опорный момент

M_Ф2= F_ПФ2 e

При сильных ветрах часть снега сносится с покрытия, и поэтому при строительстве в районах с сильными зимними ветрами расчетная снеговая нагрузка может быть снижена. Также снижается нагрузка на покры­тия зданий с неутепленной кровлей и уклоном для отвода талой воды при избыточных тепловыделениях (по СНиП 11-6-74). Схемы рам при расчете на снеговую нагрузку подобны схемам постоянной нагрузки от покрытия.

Ветровая нагрузка. В связи с тем, что скорость ветра достаточно рез­ко меняется, эта нагрузка воздействует динамически, но в низких широ­ких зданиях не появляются колебания от ветра и для них рассматрива­ется только статическая составляющая, связанная с разницей давлений внутри помещения и снаружи у стеновых (или кровельных) огражде­ний. Для высоких и узких зданий (высота более 36 м, отношение высоты к пролету более 1,5) учитывается динамическое воздействие ветра. Давление ветра на высоте 10 м над поверхностью земли в открытой местности, называемое скоростным напором ветра g_o, зависит от района строительства. Ветровая нагрузка меняется по высоте, но в нормах при­нято, что до высоты 10 м от поверхности земли скоростной напор не ме­няется. Он принят за нормативный, а увеличение его при большей вы­соте учитывается коэффициентами k, разными при разной высоте и при разных защищенностях от ветра проектируемого здания (прил. 3). За зданием (по направлению ветра) возникает зона пониженного давления и появляются поверхностная нагрузка g'₀ (отсос), направлен­ная так же, как и нагрузка g_o. Условия обтекания ветром учитываются аэродинамическими коэф­фициентами с, указанными в главе СНиП по нагрузкам и воздействиям. Таким образом, расчетная линейная ветровая нагрузка, передавае­мая на стойку рамы в какой-то точке по высоте при отсутствии продоль­ного фахверка, определяется по формуле

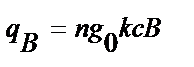
где go — нормативный скоростной напор ветра, принимаемый по СНнП П-6-74 (для некоторых городов значения go приведены в прил. 2); k — коэффициент, учитывающий высоту и защищенность от ветра другими строениями (см. прил. 3); Величина этого коэ-та зависит от площадки строительства, согласно СНиП площадки делятся на три категории

А – открытые поверхности

В – городские, защищённые зданиями, высотой более 10 м.

С - городские, защищённые зданиями, высотой более 25 м.

с—аэродинами­ческий коэффициент, зависящий от расположения и конфигурации поверхности. Для вертикальных стен с = 0,8 с наветренной стороны и с = 0,6 для отсоса; n — коэффициент перегрузки, который для зданий равен 1.2; В — ширина расчетного блока. В однопролётных зданиях, а также в многопролетных с одинаковым шагом колонн по всем рядам ширина В равна шагу рам b (рис. а). Ширина расчетного блока для многопролетного здания с разным ша­гом колонн по рядам, а также при наличии стоек фахверка показана на рис. б, в. Схема изменения ветровой нагрузки по высоте для однопролетного здания показана на рис. г. Для удобства расчета фактическую ли­нейную нагрузку (в виде ломаной прямой) можно заменить эквивалент­ной q_Э, равномерно распределенной по всей высоте. Если принять, что моменты в заделке консоли, равной по длине высоте рамы от эквива­лентной и фактической нагрузки, равны, то эквивалентные нагрузки ак­тивного давления и отсоса определяются по формулам:

С12.11)

где q_В10 — расчетная ветровая нагрузка на высоте 10 м; а — коэффициент (при H<=10 м— 1; 15 м— 1,04; 20 м — 1,1; 25 м — 1,17; 30 м — 1,23; 35 м — 1,29).

Ветровая нагрузка, действующая на участке от низа ригеля до на­иболее высокой точки здания, заменяется сосредоточенной силой, при­ложенной в уровне низа ригеля рамы. Величина этой силы от активного

 

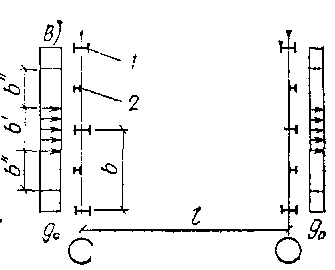
давления F_В и отсоса F'_В показана на рис г (заштрихованная часть площади эпюры):

FВ = (q₁+q₂)h//2; F'В = (q'₁+q'₂) h//2 (12.12)

Расчетная схема рамы однопролетного здания при действии вет­ровой нагрузки показана на рис д. Направление ветра может быть как в одну, так и в другую сторону. В многопролетных зданиях одинаковой высоты активное давление и отсос на наружные стойки определяют точно так же; в зданиях более сложной конфигурации или с продольным фахверком учитываются конкретные условия ветрового воздействия. Например, при наличии стоек продольного фахверка (см. рис в) на раму воздействует линейная нагрузка q_B, собираемая с ширины b', а нагрузка с ширины b" передается стойками фахверка частично на фундамент, а частично в виде сосредоточенной силы на рамы в верхних их узлах.