КУРСОВАЯ РАБОТА
по дисциплине «Математические задачи энергетики»
(Вариант - 20)
Выполнил: ст. группы ЭП-12
Тогонов В. Б.
Проверил: доцент кафедры ЭиЭТ
Грунин О.М.
Чита 2014
СОДЕРЖАНИЕ:
Введение…………………………………………………………………………….....3
1. Оптимальное распределение нагрузки между тепловыми электростанциями (ТЭС)…………………………………………………………………….……………..4
1.1. Найти экономичное распределение нагрузки между тремя ТЭС без учета технических ограничений………………………………………….…..……………..5
1.2. Найти экономичное распределение нагрузки между тремя ТЭС с учетом технических ограничений……………………………………………………….……7
2. Оптимальное размещение компенсирующих устройств…….………………..…8
3. Выбор оптимальной конфигурации сети………………………………….…….12
Выводы по проделанной работе……………………………………...……………..17
Введение
Цель данной курсовой работы состоит в том, чтобы ознакомить студента с математическими методами расчета электрических систем и сетей, дать общее представление о тех проблемах и задачах, которые решаются данными методами, повторить и закрепить на практике ранее изученные курсы высшей математики и теоретических основ электротехники.
Поскольку проект имеет тематику, непосредственно связанную с будущей специальностью и профессией, считаю его выполнение важным и актуальным с точки зрения введения в специфику профессии, а также углубления понимания того, какие должностные обязанности мне необходимо будет выполнять.
Задание 1. Оптимальное распределение нагрузки между тепловыми электростанциями (ТЭС)
Исходные данные: 
Рис.1. Схема распределения нагрузки между тремя ТЭС
Коэффициенты относительных приростов ТЭС:
a1=0.525, a2=0.35, a3=0.7, b1=2.842, b2=1.274, b3=4.164.
Допустимые границы изменения мощностей:
P1min=0.15, P2min=0.4, P3min=0.1
P1max=0.35, P2max=0.6, P3max=0.35.
Задача 1. Найти экономичное распределение нагрузки P∑=PН1+PН2+PН3 между тремя ТЭС без учета технических ограничений
Решение:
Характеристика относительных приростов (ХОП)
Ej (Pj) = 0.3 + ajPj + bjPj2,
где Pj – мощность ТЭС-j в относительных единицах;
aj, bj – коэффициенты ХОП;
j = 1, 2, 3
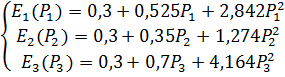
k=0
Зададим начальное приближение 
= 
Найдём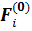 
= 
; 
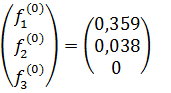Найдём численные значения элементов матрицы Якоби:
J ( 
;
Найдём вектор поправок:
J ( 
× 
;
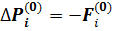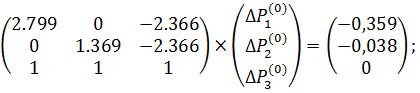
Мощности с учётом поправок:
Результат следующей итерации, приведен в таблице 1.
Таблица 1. Результаты выполненных итераций
| k | Pk |  Pk
| Fk | 
| ||||||
| P1 | P2 | P3 | P1
| P2
| P3
| F1 | F2 | F3 | ||
| 0 | 0,4 | 0,4 | 0,2 | -0,0913 | 0,0477 | 0,0436 | 0,359 | 0,038 | 0 | 0,361 |
| 1 | 0,309 | 0,447 | 0,244 | -0,0089 | 0,0084 | 0,0006 | 0,022 | -0,011 | 0 | 0,025 |
| 2 | 0,3001 | 0,4554 | 0,2446 | 0,0016 | -0,0337 | -0,0009 | -0,006 | 0,0025 | 0,0027 | 0,007 |
| 3 | 0,303 | 0,451 | 0,246 | - | - | - | - | - | - | - |
Задача 2. Найти экономичное распределение нагрузки P∑=P1+P2+P3 между тремя ТЭС с учетом технических ограничений
;
;
За рамки технических ограничений не выходят все три мощности станций,
поэтому мощности ТЭС с учётом технических ограничений:
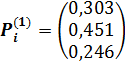
Задание 2. Оптимальное размещение компенсирующих устройств
Эффективно распределить мощность БСК на шинах НН ТП 1,…,4. Критерий оптимальности – минимум потерь активной мощности. Суммарная мощность БСК равна Qk. Мощности Qkj (j=1,…,4) должны отвечать условию 0 
и быть кратными 25 кВАр.
Исходные данные:
Рис.2.1. Схема сети 10 кВ
Мощности нагрузок, кВА:
Н1=310+j270; H2=210+j150; H3=800+j500; H4=660+j350;
Номинальные мощности трансформаторов, кВА:
Т1=400; Т2=250; Т3=1000; Т4=630;
Общая мощность БСК, кВАр:
Qk=625;
Параметры ВЛ:
Марка провода – А-70;
r0=0,42 (Ом/км)
Л1=1,6 (км); Л2=1,2 (км); Л3=1,8 (км); Л4=2,4 (км);
RT1=3,44 (Ом); RT2=1,22 (Ом); RT3=5,92 (Ом); RT4=1,91 (Ом)
Решение:
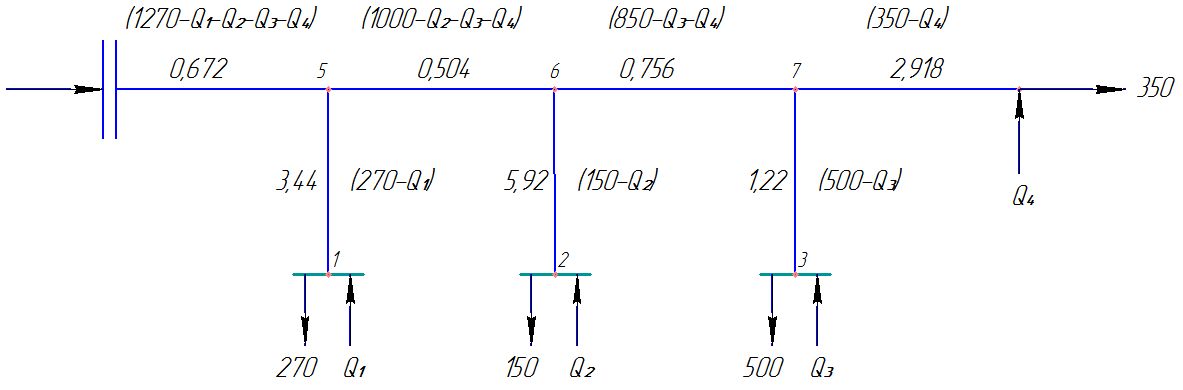
Рис.2.2. Преобразованная схема
Запишем функцию Лагранжа:
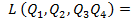
– произвольные начальные значения мощностей БСК
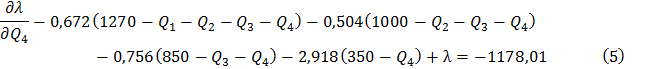
(6)
Считаем 
:
1) 100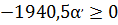 
2) 100 
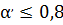
3) 150 
4) 200 
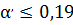
Выбираем 
и подставляем в уравнение (6):
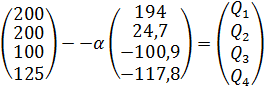
1)Пусть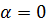 
, тогда
2)Пусть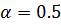 
, тогда
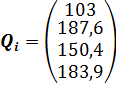
3)Пусть 
, тогда
Результаты дальнейшего расчёта сведены в таблицу 2.
Таблица 2. Результаты выполненных итераций
| k | 
| 
| ||||||||
| Q1 | Q2 | Q3 | Q4 | 1
| 2
| 3
| 4
| 
| 
| |
| 1 | 200 | 200 | 100 | 125 | 1940,5 | 247 | -1009,5 | -1178,01 | 2496,7 | 5,58 |
| 2 | 31,6 | 178,6 | 187,6 | 227,2 | -617 | 784 | -94,9 | -72,1 | 1234,6 | 4,35 |
| 3 | 106,4 | 83,6 | 199,1 | 235,9 | - | - | - | - | - | 3,96 |
Полученное решение округлим до ±25
; 
;
Задание 3. Выбор оптимальной конфигурации сети
Необходимо выбрать линии на такие пропускные способности Xij, чтобы суммарные потери были минимальны.
