Несмещённость – при увеличении объёма выборки оценка должна сходиться по вероятности и истинному значению параметра.
Согласованность – S2 – смещённая дисперсия. Смещение этой характеристики происходит из-за того, что отклонение выборочного значения отсчитывается не от математического ожидания теоретического распределения, а от его эмпирического аналога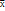 
ср, поэтому вводят поправку для получения несмещённой дисперсии (
).
Достаточность – число выборочных значений, которая отражала бы закон распределения всей совокупности.
Мера положения – 1 момент (арифметическое, геометрическое, гармоническое средние, медиана, мода)
Сре́днее арифмети́ческое — это сумма всех чисел в наборе, делённая на их количество (μ).
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X.
Гармоническое среднее – (среднее степенное) среднее значение: 
Медиана – среднее значение в группе измерений, когда они выстроены в порядке возрастания; если число показаний четное, то по соглашению это среднее двух центральных значений (
).
Мода – значение x, эмпирическая вероятность mi/n которого максимальна; находится графически по гистограмме или с помощью линейной интерполяции.
Рисунок 1 – Симметричное распределение
Рисунок 2 – Распределение с асимметрией
Меры рассеивания (дисперсия, стандартное отклонение, размах)
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается D [ X ], 
или 
. 
Среднеквадрати́ческое отклоне́ние — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. 
Стандартное отклонение (несмещённая оценка среднеквадратичного отклонения случайной величины x относительно её математического ожидания): 
Размах - расстояние xn- x1 между крайними членами вариационного ряда. Применяется при построении контрольных карт распределения значений выборки.
4) Меры формы
Вариационный ряд - реализации, записанные не в порядке получения, а в порядке возрастания, то есть упорядоченная выборка Выборка - совокупность объектов, отобранных для исследования из генеральной совокупности, а их число n- объём выборки
Доверительный интервал Jγ
интервал, накрывающий параметр с вероятностью γ (γ – доверительная вероятность или уровень доверия)
Математическая статистика - раздел математики, посвящённый математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов
Математическое ожидание - аналог понятия центра масс, то есть «средневзвешенное» значение случайной величины
Математическое ожидание дискретной случайной величины x
сумма произведений всех ее возможных значений на их вероятности:
Метод моментов метод получения оценок параметров, который состоит в том, что если оцениваемый параметр распределения является функцией от моментов распределения (в самом простом случае сам является моментом), то в эту функцию подставляются эмпирические значения Статистика - любая функция q(x1,¼, xn), зависящая от выборки; является случайной величиной
моментов и полученное значение берется в качестве оценки для параметра
Функция распределения F(x) - функция, применяемая для задания случайной величины, равная вероятности того, что случайная величина x примет значение, меньшее х: F(x) = p(x<x)
