ДЛЯ ФЗО
Варианты выбираются на основе набора вариантов двух задач 101-200, 201(NM). Номер NM соответствует двум последним цифрам зачетки для первой задачи и последней цифре зачетки для второй задачи.
Пример варианта: 113; 201(13), если две последние цифры зачетки 13.
Блок 1.
Современная математическая теория оптимизации. Решение задач линейного программирования –из набора 101-200 соответственно.
Пример 1. Найти оптимальный план исходной задачи, доставляющий предприятию максимальный доход.
Целевая функция имеет вид
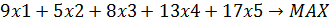
Ограничения задачи
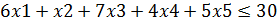
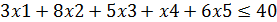
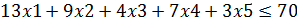
Приведем пример решения задачи в системе Excel данных через функцию «Поиск решения»
| Ограничения | ai1 | ai2 | ai3 | ai4 | ai5 | bi | |
| a 1j | |||||||
| a2j | |||||||
| a3j | |||||||
| Целевая функция | cj | ||||||
| x1 | x2 | x3 | x4 | x5 | |||
| Переменные решения | 6,375 | 0,875 | |||||
| Ограничение 1 | 41,75 | ||||||
| Ограничение 2 | |||||||
| Ограничение 3 | |||||||
| Целевая функция | 86,125 |
1. Найти оптимальный план исходной задачи, доставляющий предприятию максимальный доход.
Ответ: оптимальный план составляет
| x1 | x2 | x3 | x4 | x5 |
| 6,375 | 0,875 |
При этом доход равняется 86,125 условных единиц.
Для ответов на вопросы 2-4 необходимо построить отчет по устойчивости линейной модели.
Отчет по устойчивости линейной модели.
| Ячейка | Имя | Результ. значение | Нормир. стоимость | Целевой коэффициент | Допустимое увеличение | Допусти-мое уменьшение | |
| $C$8 | Переменные решения x1 | 6,375 | 3,75 | ||||
| $D$8 | Переменные решения x2 | -21,3125 | 21,3125 | - | |||
| $E$8 | Переменные решения x3 | -8,3125 | 8,3125 | - | |||
| $F$8 | Переменные решения x4 | 0,875 | 5,8 | ||||
| $G$8 | Переменные решения x5 | -12,4375 | 12,4375 | - | |||
| Ячейка | Имя | Результ.значение | Теневая Цена | Ограничение правая часть | Допустимое увеличение | Допусти-мое уменьшение | |
| $C$9 | Ограничение 1 x1 | 41,75 | - | 3,25 | |||
| $C$10 | Ограничение 2 x1 | 1,8125 | 2,364 | 14,57 | |||
| $C$11 | Ограничение 3 x1 | 1,3125 | 8,667 | 4,667 |
2. Оценить рентабельность продукции и ее цену, характеристики которой 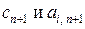 представлены отдельным столбцом, справа от основных таблиц.
представлены отдельным столбцом, справа от основных таблиц.
Ответ. В данном случае рентабельным будет только производство продукции 1 и 4 типа, цена которых составляет соответственно 12 и 11 условных единиц.
3. Найти интервалы изменения коэффициентов целевой функции, в пределах которых ассортимент выпускаемой продукции не меняется.
Ответ: интервалы изменения коэффициентов целевой функции находятся, если к столбцу коэффициентов целевой функции (столбец 5, строки от 2 до 6) прибавят или вычтут соответственно значения допустимого увеличения и допустимого уменьшения.
4. Найти интервалы изменения ресурсов, в пределах которых сохраняется устойчивость двойственных оценок.
Ответ: интервалы изменения ресурсов, в пределах которых сохраняется устойчивость двойственных оценок находятся, если к столбцу коэффициентов целевой функции (столбец 5 строки от 9 до 11) прибавят или вычтут соответственно значения допустимого увеличения и допустимого уменьшения.
Задачи 101 – 200
Ниже приведены комплексные задачи линейного программирования. Необходимо выполнить в указанном порядке следующие задания.
1. Найти оптимальный план прямой задачи графическим методом.
2. Построить двойственную задачу.
3. Найти оптимальный план двойственной задачи из графического решения прямой, используя условия дополняющей нежесткости.
4. Найти оптимальный план прямой задачи с применением функции поиска решения в Excel.
5. Дать интерпретацию изменения решения (по отчету на устойчивость) при условии изменения коэффициентов целевой функции на (N/3)% и (N/2)% соответственно.
6. Показать изменения оптимального плана при изменении правой части первого из ограничений задачи в системе уравнений на 6%. Сравнить результаты с результатом, полученный графическим методом (см. п.1).
7. Найти наиболее дефицитные ресурсы и показать возможности повышения дохода предприятия путем увеличения запаса дефицитного ресурса. Обосновать свой выбор по отчету на устойчивость из п.5.
 101 101
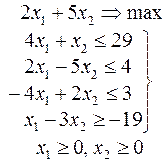
|
|
|
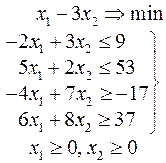
|
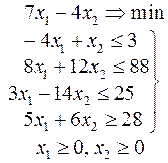
|
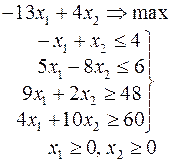
|
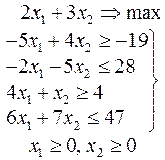
|
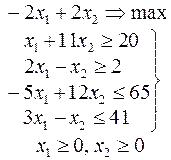
|
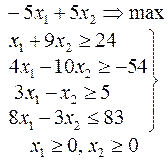
|
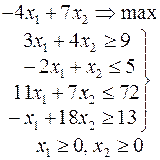
|
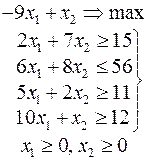
|
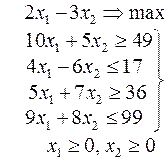
|
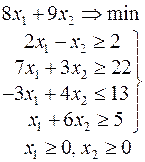
|
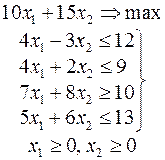
|

|
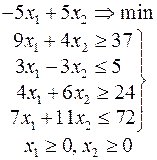
|
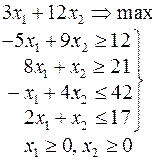
|
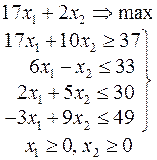
|
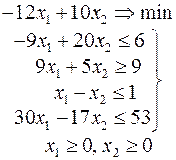
|
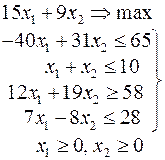
|
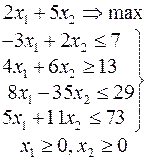
|
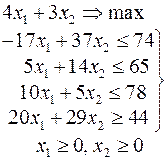
|
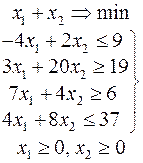
|
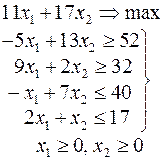
|
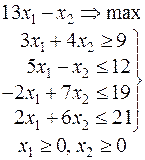
|

|
|
|
|
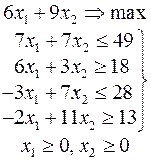
|
|
|
|

|
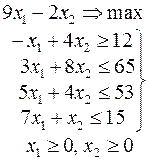
|
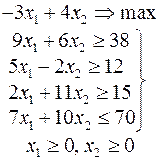
|
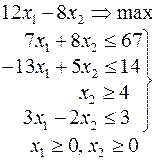
|
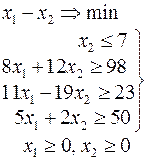
|
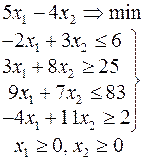
|
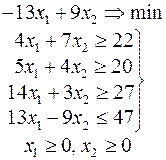
|
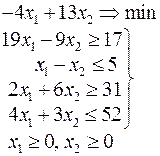
|
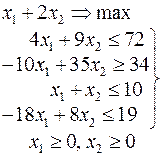
|
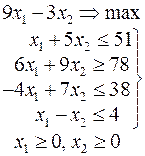
|
|
|
|
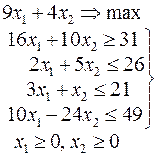
|
|
|
|
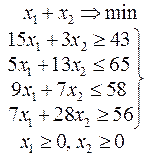
|
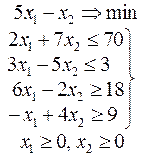
|
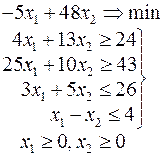
|
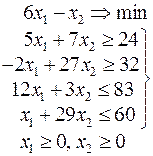
|
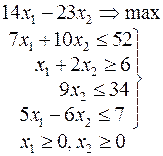
|
|
|
|
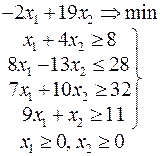
|
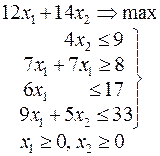
|
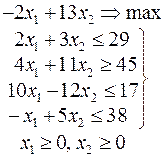
|
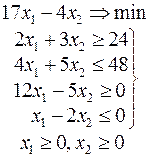
|
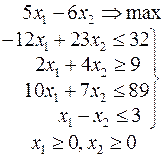
|
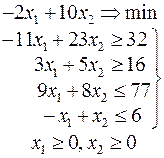
|
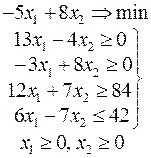
|
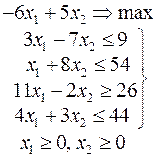
|
|
|

|
|

|
|
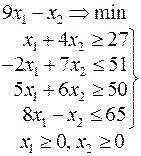
|
|
|
|
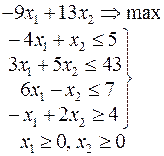
|
|
|
|
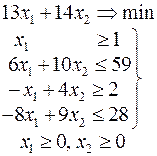
|
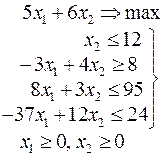
|
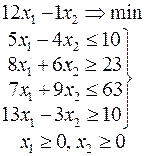
|
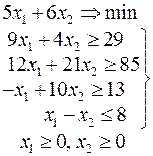
|
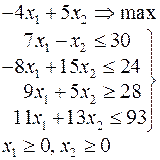
|
|
|
|
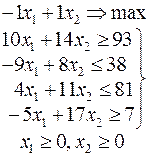
|
|
|
|
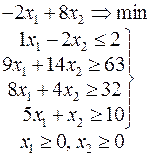
|
|
|
|
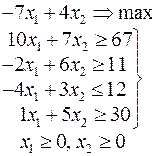
|
|
|
|






