Иррациональные уравнения
Иррациональным уравнением называется уравнение, содержащее неизвестное под знаком корня.
При решении иррациональных уравнений применяют метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
Следует учесть, что при возведении обеих частей уравнения в чётную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней подстановкой в исходное уравнение. Необходимо иметь в виду, что избавиться от иррациональности вида n 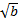
можно возвести в степень n,так как (n 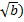 n=b. Этим приёмом нельзя избавиться от иррациональности в выражении n
n=b. Этим приёмом нельзя избавиться от иррациональности в выражении n 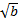 +с.
+с.
I. Уравнения, содержащие квадратные корни.
Для решения таких уравнений надо:
1) возвести обе части уравнения в квадрат;
2) упростить полученное уравнение;
3)при необходимости ещё раз возвести в квадрат и т. д. до тех пор, пока не получится уравнение, не содержащее корни.
4) решить это уравнение;
5) сделать проверку или определить область допустимых значений для неизвестного числа; отобрать соответствующие корни (решения)
6) записать ответ.
Пример 1. Решить уравнение  =2х-1
=2х-1
Решение.
В левой части уравнения находится только квадратный корень. Возьмём обе части уравнения в квадрат:
( )2=(2х-1)2
)2=(2х-1)2
х2+5х+1= 4х2-4х+1
3х2-9х=0
Х2-3х=0
х(х-3)=0
х1=0; х2=3
Проверка:
х1=0: 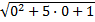 =1; 2·0-1=-1; 1≠-1 =>х1=0 не является корнем уравнения (посторонний корень).
=1; 2·0-1=-1; 1≠-1 =>х1=0 не является корнем уравнения (посторонний корень).
х2=3:  =5; 2·3-1=5; 5=5.
=5; 2·3-1=5; 5=5.
Ответ: х =3.
Пример 2. Решить уравнение 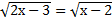
Решение.
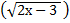 2
2 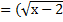 )2
)2
2х-3=х-2
2х-х=3-2
Х=1
Проверка:
Х=1: 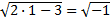 не существует => х=1-посторонний корень. Поэтому данное уравнение не имеет решений.
не существует => х=1-посторонний корень. Поэтому данное уравнение не имеет решений.
Ответ: решений нет.
Пример 3. Решить уравнение 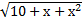 -х=4х-4
-х=4х-4
Решение.
Оставим в левой части только слагаемое с квадратным корнем
 =х+3х-4
=х+3х-4
 =4 х -4
=4 х -4
 2=(4х-4)2
2=(4х-4)2
10+х+х2=16х2-32+16
15х2-33х+6=0
Получили квадратное уравнение, решим его.
D= 
D=332- 4·15·6=1089-360=729
Х12 
Х12 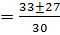 х1=2; х2=0,2
х1=2; х2=0,2
Проверка:
х1=2: 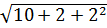 -2 =
-2 = 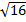 - 2= 4- 2=2; 3·2-4=2; 2=2
- 2= 4- 2=2; 3·2-4=2; 2=2
х2=0,2: 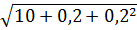 =
= 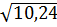 -0,2=3,2-0,2=3; 3·0,2-4=0,6-4= -3,4;
-0,2=3,2-0,2=3; 3·0,2-4=0,6-4= -3,4;
3≠-3,4 => [1]х2=-3,4- посторонний корень.
Ответ: х =2.
Пример 4. Решить уравнение 
Решение.
Возьмём обе части уравнения в квадрат:
(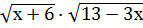 )2=(х+3)2
)2=(х+3)2
(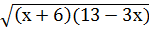 )2 =(х+3)2
)2 =(х+3)2
(х+6)(13-3х) = (х+3)2
13х-3х2+78-18х=х2+6х+9
4х2+11х-69=0
х1=3; х2= 
Проверка:
х1=3: 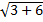 ·
· 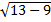 =3·2=6 3+3=6; 6=6.
=3·2=6 3+3=6; 6=6.
х2= 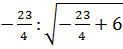 ·
· 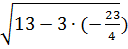 = -
= - 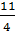
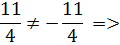 х2=
х2=  - посторонний корень
- посторонний корень
Ответ: х =3.
Пример 5. Решить уравнение 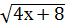 -
- 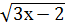 =2
=2
Решение.
Здесь нельзя избавиться от иррациональности сразу. Возведение обеих частей равенства в квадрат приводит к новому иррациональному уравнению.
(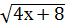 -
- 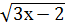 )2 =22
)2 =22
4х+8-2 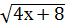 ·
· 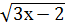 +3х-2=4
+3х-2=4
7х=2=2 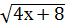 ·
· 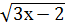
Возводим ещё раз в квадрат:
(7х+2)2=(2 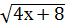 ·
· 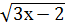 )2
)2
49Х2+28Х+4=4·(4Х+8)(3Х-2)
49Х2+28Х+4=4·(12х2-8х+24х-16)
х2-36х+68=0
х1=34; х2=2
Проверка:
х1=34: 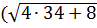 -
- 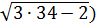 =
= 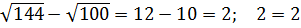
х2=2: 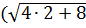 -
-  =
= 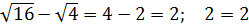 .
.
Ответ: х =34; х2=2.
Пример 6. Решить уравнение  =
= 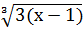 .
.
Решение.
( )3 =(
)3 =(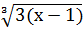 )3
)3
2х+7=3х-3
2х-3х=-3-7
-х=-10
х=10
Заметим, что в данном случае проверка необязательна, так как использовался метод возведения обеих частей в нечётную степень, при котором посторонние корни не появляются.
Ответ: х =10.
Пример7. Решить уравнение 4  =х
=х
Решение.
(4  )4 = (х)4
)4 = (х)4
25х2-144=х4
х4-25х2+144=0 - биквадратное уравнение.
Пусть х2=у, тогда у2-25у+144=0
Находим у1=16; у2=9. Поэтому: х2=16 => х1,2=±4 и
х2=9=> х3,4=±3
Проверка: х1=4: 4 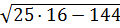
 =
=  =4; 4=4.
=4; 4=4.
х2=-4: 4 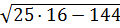 =
=  =4; 4≠-4=> х2=-4 - посторонний корень.
=4; 4≠-4=> х2=-4 - посторонний корень.
х3=3: 4  =
= 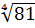 =3; 3=3.
=3; 3=3.
х4=-3 4  =
= 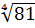 =3; 3≠-3- посторонний корень.
=3; 3≠-3- посторонний корень.
Ответ: х1=4;х2=3.
Пример8. Решить уравнение 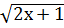 +
+ 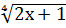 =12.
=12.
Решение.
Пусть 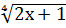 = у, тогда
= у, тогда 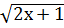 = (
= (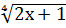 )2=у2.
)2=у2.
Поэтому у2+у-12=0; у1=3; у2=-4
1) 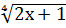 =3
=3
2х+1=34
2х+1=81
2х=80
х=40.
2) 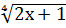 =-4. Это уравнение не имеет корней, так как
=-4. Это уравнение не имеет корней, так как
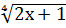 ≥0, а число (-4)˂0.
≥0, а число (-4)˂0.
Проверка: х=40: 
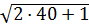 +
+  =
= 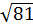 +
+ 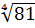 =9+3=12; 12=12.
=9+3=12; 12=12.
Ответ: х=40
Пример9. Решить уравнение

Решение.
Область определения уравнения: х≠±13.
Пусть  = у, тогда
= у, тогда
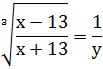
у≠0.
Поэтому 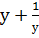 =
= 
3у2-10у+3=0; у1=3; у2=  . Отсюда:
. Отсюда:
1) 
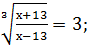
 3;
3; 
х+ 13=27·(х-13);
х+13=27х-351
26х = 364
х1=14;
2) 


27·(х+13)=х-13
27х+351=х-13
26х=-364
х2=-14.
Ответ: х1=14; х2=14.·
Упражнения для самостоятельной работы
Решить уравнения:
1. 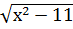 =-х-1;
=-х-1;
2. 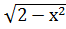 -
- 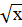 =0;
=0;
3.  -х=1;
-х=1;
4. 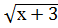 -
- 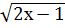 =х+1;
=х+1;
5. 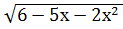 -4=х;
-4=х;
6.  +
+ 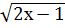 =3;
=3;
7. 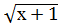 +
+ 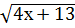 =
= 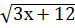
8. х2= 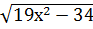
9. 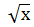 +
+  =20;
=20;
10. 2 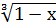 =5·
=5· 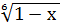 -18=0;
-18=0;
11. 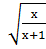 +2·
+2· 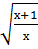 =3;
=3;
12. 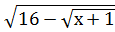 =4;
=4;
13. 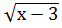 -
- 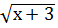 =2-
=2-  ;
;
14. 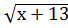 =12-
=12- 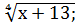
15. 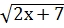 - 2 = х.
- 2 = х.
Ответы:
1.х=-6; 2.х=1;
3. х1=2, х2=0; 4. х=1;
5. х1=-1, х2= 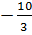 ; 6.х=1;
; 6.х=1;
7. х=-1; 8.х1,2= 
 , х3,4=
, х3,4=  ;
;
9. х=256; 10. х=-63;
11.  ; 12. х=-1;
; 12. х=-1;
13. х=7; 14. х=68;
15. х=1






