Прискорення — векторна величина. Його напрямок не завжди збігається із напрямком швидкості. В загальному випадку вектор прискорення утворює з вектором швидкості деякий кут і розкладається на дві складові. Складова вектора прискорення, яка направлена паралельно до вектора швидкості, а, отже, вздовж дотичної до траєкторії, називається тангенціальним прискоренням. Складова вектора прискорення, що направлена перпендикулярно до вектора швидкості, а, отже, вздовж нормалі до траєкторії, називається нормальним прискоренням.
.
Перший член у цій формулі задає тангенціальне прискорення, другий - нормальне, або доцентрове. Зміна напрямку одиничного вектора завжди перпендикулярна до цього вектора, тому другий член в цій формулі нормальний до першого.
У випадку обертання тіла по колу зі швидкістю, що не змінюється за модулем, вектор прискорення перпендикулярний до вектора швидкості.
3.В основі динаміки, яка розглядає закони руху тіл і ті причини, що його викликають або змінюють, лежать закони Ньютона. Перший закон Ньютона (закон інерції)
Цей закон також має назву закону інерції або принципу Галілея. Строге його формулювання в сучасному викладі таке:
§ Існують такі системи відліку, в яких центр мас будь-якого тіла, на яке не діють ніякі сили або рівнодійна діючих на нього сил дорівнює нулю, зберігає стан спокою або рівномірного прямолінійного руху, допоки цей стан не змінять сили, застосовані до нього.
Цей закон є спеціальним випадком другого закону Ньютона (дивись нижче), але його значення полягає в тому, що він визначаєсистеми відліку, в яких справедливі наступні два закони. Ці системи відліку мають назву інерційних або Галілеєвих, тобто таких, які рухаються зі сталою швидкістю одна відносно іншої.
[ред.]Другий закон Ньютона: базовий закон динаміки
Формулювання:
§ Прискорення матеріальної точки прямо пропорційне силі, яка на неї діє, та направлене в сторону дії цієї сили
Математично це формулювання може бути записано так:
або
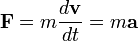, якщо m — константа.
де
§ F — сила, яка діє на тіло
§ m — маса тіла
§ a — прискорення
§ v — швидкість
§ m v — імпульс, який також позначається як 
Це рівняння фактично означає, що чим більша за абсолютним значенням сила буде прикладена до тіла, тим більшим буде його прискорення. Параметр m або маса в цьому рівнянні — це насправді коефіцієнт пропорційності, який характеризує інерційні властивості об'єкта.
У рівнянні F = m a прискорення може бути безпосередньо виміряне, на відміну від сили. Тому цей закон має сенс, якщо ми можемо визначити силу F безпосередньо. Одним з таких законів, який визначає правило обчислення гравітаційної сили, є закон всесвітнього тяжіння.
У загальному випадку, коли маса та швидкість об'єкта змінюються з часом, отримаємо:
Рівняння із змінною масою описує реактивний рух. лат. Важливе фізичне значення цього закону полягає в тому, що тіла взаємодіють, обмінюючись імпульсами й роблять це за допомогою сил.
[ред.]Третій закон Ньютона: закон дії та протидії
Формулювання:
Сили, що виникають при взаємодії двох тіл, є рівними за модулем і протилежними за напрямом.
Математично це записується так
,
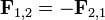де 
— сила, що діє на перше тіло з боку другого тіла, а 
— навпаки, сила, що діє з боку першого тіла на друге тіло.
Суперечливого формулювання «на всяку дію є рівна протидія» слід уникати.
Закон у сформульованій формі є справедливим для усіх фізичних сил, хоча існують деякі особливості формулювання цього закону в застосуванні до сил електромагнітного поля.
4. Iмпульсом або вектором кількості руху в класичній механіці називається міра механічного руху тіла, векторна величина, що для матеріальної точки дорівнює добуткумаси точки на її швидкість та має напрямок швидкості.
У системі СІ одиницею вимірювання імпульсу є кг·м/с, в системі СГС — [г·см/с].
Сума імпульсу для будь-якої замкнутої системи є величиною сталою.
Закон збереження імпульсу - один із фундаментальних законів фізики, який стверджує, що у замкненій системі сумарнийімпульс усіх тіл зберігається.
Якщо на систему тіл зовнішні сили не діють або вони врівноважені, то така система називається замкненою, для неї виконується закон збереження імпульсу: повний імпульс замкненої системи тіл залишається незмінним за будь-яких взаємодій тіл цієї системи між собою:
Закон збереження імпульсу є наслідком однорідності простору.
[ред.]Доведення
Розглянемо систему із N тіл, які взаємодіють між собою. Силу, яка діє на i-те тіло з боку j-ого тіла позначимо 
. Рівняння руху для кожного із N тіл записуються у вигляді:
,
де 
- імпульс i-ого тіла.
Просумувавши усі рівняння, й враховуючи те, що за третім законом Ньютона
,
отримуємо:
,
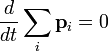звідки
,
тобто сумарний імпульс є інтегралом руху.
