Этапы решения
· Создание трехмерной модели в среде трехмерного моделирования + чертеж модели с размерностью зон теплообмена;
· создание КЭМ поршня, задание кинематических ГУ и ГУ контакта, задание ГУ теплообмена;
· решение стационарной задачи теплопроводности для режима холостого хода;
· решение стационарной задачи теплопроводности для режима номинальной мощности;
· создание исследования переходного термического процесса;
· анализ температурного состояния поршня для обоих режимов, создание графиков изменения температуры на поверхности поршня в радиальном и осевом направлении. Вычерчивание графиков термических результатов относительно времени.
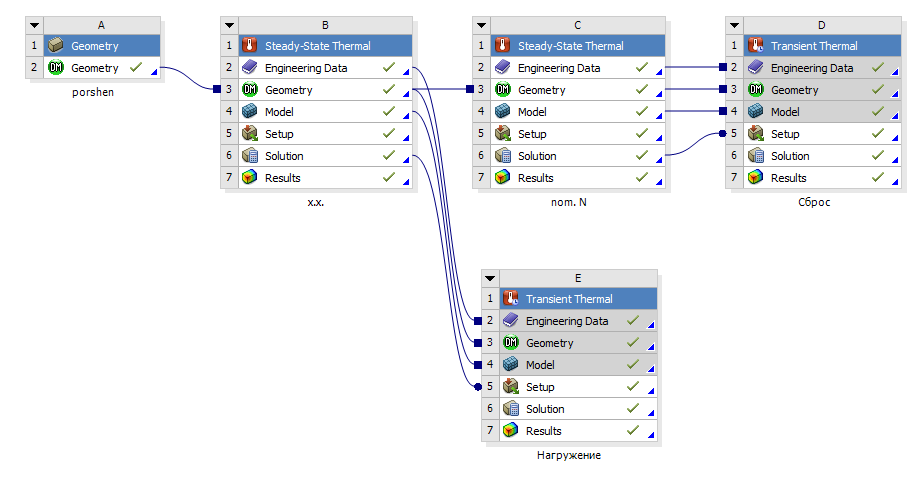
Рис.1 Схема проекта
Стационарное тепловое нагружение поршня
Задача определения поля температур связана с решением уравнения теплопроводности, которое при постоянных теплофизических характеристиках материала имеет вид
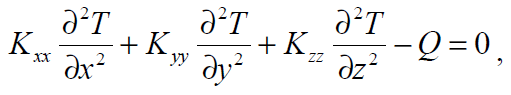
где Kxx, Kyy, Kzz – коэффициенты теплопроводности материала поршня в соответствующих направлениях, Вт/(м*К); Q – количество теплоты, выделяющейся в единице объема внутренними источниками теплоты (при их наличии).
Уравнение при использовании МКЭ преобразуется к системе линейных уравнений. Узловые температуры конечноэлементной модели поршня определим после решения этой системы уравнений
[K]{T}+ {F}= 0,
где [K]– матрица теплопроводности КЭМ;
{F} – вектор тепловой нагрузки КЭМ.
Для решения задачи о тепловом состоянии поршня необходимо задать граничные условия теплообмена на его поверхности. В качестве основных ГУ, описывающих тепловое взаимодействие поверхностей поршня и окружающей среды, используются следующие:
условие I рода – распределение температуры на поверхности F
Т=Тп(x,y,z)
где Tп (x, y, z) – заданная на поверхности поршня функция температуры,
полученная с помощью обработки индикаторной диаграммы или результатов термометрирования поршня;
условие II рода – плотность теплового потока q0 через поверхность F или часть ее
,
где n – внешняя нормаль к поверхности тела в точке с координатами x, y, z;
условие III рода – температура окружающей среды T и закон теплообмена α между средой и поверхностью поршня F
∂ 
,
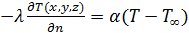где α– коэффициент теплоотдачи с окружающей средой на поверхности поршня, Вт/(м2·К); T,T∞ – температура в определенной точке поршня и температура окружающей среды над этой точкой, K; λ– коэффициент теплопроводности материала поршня, Вт/(м*К).
Для расчета теплового состояния поршня принято задавать ГУ I и III рода.
Для определения численного значения коэффициента теплоотдачи α на поверхности камеры сгорания поршня в качестве исходного уравнения могут использоваться критериальные уравнения Г. Вошни
,
если выражение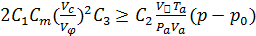 
,
то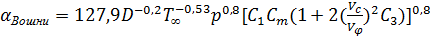 
Здесь в уравнении 
– для процессов газообмена;
– для процессов сжатия – сгорания – расширения;
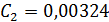– для дизелей с непосредственным впрыскиванием, м/(с·К);
.
Кроме того, при определении коэффициентов теплоотдачи рекомендуется использовать также зависимость Г. Хохенберга
,
где C1=130 и C2=1,4.
В формулах Ta – температура рабочего тела в начале такта сжатия, К; D – диаметр цилиндра, м; p, p0, pa – текущее давление в цилиндре, окружающей среды и начала сжатия, бар; Cm – средняя скорость поршня, м/с; Va,Vc,Vφ,Vh – объем цилиндра в начале такта сжатия, сгорания, а также текущий и рабочий объем цилиндра, м3; αB– коэффициент избытка воздуха; Cu /Cm – отношение тангенциальной скорости вращающегося заряда к средней скорости поршня.
Поскольку формулы Вошни и Хохенберга не позволяют получить
удовлетворительные результаты, то хорошее совпадение значений α с экспериментальными данными вероятно при использовании среднеарифметического их значения
(αВошни+αХохенберга)/2.
В некоторых случаях можно воспользоваться следующей зависимостью для определения коэффициента теплоотдачи со стороны КС (формула Эйхельберга)
,
где Ta – температура начала сжатия, К; Cm – средняя скорость поршня, м/с;
Pe – среднее эффективное давление, кг/см2 (1 МПа = 10 кг/см2).
