По мере развития техники появлялись разные способы кодирования информации. Во второй половине XIX века американский изобретатель Сэмюэль Морзе изобрел удивительный код, который служит человечеству до сих пор. Информация кодируется тремя символами: длинный сигнал (тире), короткий сигнал (точка), нет сигнала (пауза) - для разделения букв.
Своя система существует и в вычислительной технике - она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1. Эти знаки называются двоичными цифрами, по-английски - binary digit или сокращенно bit (бит).
Одним битом могут быть выражены два понятия: 0 или 1 (да или нет, черное или белое, истина или ложь и т.п.). Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия:
00 01 10 11
Тремя битами можно закодировать восемь различных значений:
000 001 010 011 100 101 110 111
Увеличивая на единицу количество разрядов в системе двоичного кодирования, мы увеличиваем в два раза количество значений, которое может быть выражено в данной системе, то есть общая формула имеет вид:
N=2^m
где N - количество независимых кодируемых значений;
m - разрядность двоичного кодирования, принятая в данной системе.
M N
1 2
2 4
3 8
4 16
....
8 256
Системы счисления бывают позиционные и непозиционные.
Непозиционные системы счисления - это системы, в которых значение символа не зависит от его места расположения в числе.
Позиционные системы счисления - это системы. в которых значение символа зависит от его места расположения в числе.
Основание системы счисления
Коль скоро мы утверждаем, что система счисления основывается на ограниченном количестве цифр, осталось задаться вопросом "сколько", какое количество цифр достаточно для решения этой проблемы.
Оказывается, что минимальное количество цифр действительно существует, а максимальное — нет, точнее, оно ограничено не принципиальными причинами, а сугубо практическими (или какими-то условиями уже не математического свойства). В данный момент важно понять, что существует не одно множество цифр, образующих систему счисления. Это множество получило особое название — основание системы счисления.
Определение
Основание позиционной системы счисления — это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе.
Выбор количества цифр диктуется какими-либо потребностями реальной жизни, науки или удобствами обработки. Исторически этот выбор определялся привычками или традициями конкретного народа.
Пример
В Великобритании до недавнего времени была принята не десятичная система веса, длины, а использовались "допотопные" ярды, футы, дюймы и т. д. Только несколько лет назад английский парламент принял решение о переходе на десятичную систему, т. е. на метры, сантиметры и т. п. И поскольку англичане — очень консервативный народ, такой переход, возможно, будет продолжаться не один десяток лет. Как сказано выше, систем счисления может быть неограниченое количество. По значению этого основания и называются системы счисления. Мы рассмотрим только некоторые их них.
Перевод из 10-ой системы счисления в 2-ую, 8-ую, 16-ую.
Чтобы перевести число из десятичной системы в двоичную(8-ую, 16 -ую) надо производить последовательное деление на 2 (8, 16) до тех пор пока в частном не получиться число меньше делителя.
В качестве результата записать последние значения частного и выписать за ним все остатки в обратном порядке.
1. Способ: 1) 40(10)= > 101000(2) 2) 123(10)=>173(8) 3) 123(10)=>7B
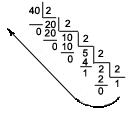


2. Способ: 71(10)=> 100111(2)
71|1
35|1
17|1
8 |0
4 |0
2 |0
1
9. Система счисления - это изображение или запись числа с помощью различных знаков и цифр.
Разделяют системы счисления позиционные и непозиционные.
Непозиционные – в них значение каждой цифры не зависит от ее положения в ряду цифр, изображающих число.
I-1 V-5 X-10 L-50 C-100 В-500 M-1000
Позиционные - в них значения каждой цифры зависит от ее положения в ряду цифр, изображающих число.
Основания сс - это количество цифр и символов для записи любого числа называется базой сс






