6.5.1 Расчет железобетонных элементов по деформациям производят из условия, по которому прогибы или перемещения конструкций f от действия внешней нагрузки не должны превышать предельно допустимых значений прогибов или перемещений fult
f ≤ fult. (6.6)
6.5.2 Прогибы или перемещения железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных (жесткостных) характеристик железобетонного элемента в сечениях по его длине (кривизны, углов сдвига и т.д.).
6.5.3 В тех случаях, когда прогибы железобетонных элементов в основном зависят от изгибных деформаций, значения прогибов определяют по жесткостям или по кривизнам элементов.
Жесткость рассматриваемого сечения железобетонного элемента определяют по общим правилам сопротивления материалов: для сечения без трещин - как для условно упругого сплошного элемента, а для сечения с трещинами - как для условно упругого элемента с трещинами (принимая линейную зависимость между напряжениями и деформациями). Влияние неупругих деформаций бетона учитывают с помощью приведенного модуля деформаций бетона, а влияние работы растянутого бетона между трещинами - с помощью приведенного модуля деформаций арматуры.
Кривизну железобетонного элемента определяют как частное от деления изгибающего момента на жесткость железобетонного сечения при изгибе.
Расчет деформаций железобетонных конструкций с учетом трещин производят в тех случаях, когда расчетная проверка на образование трещин показывает, что трещины образуются. В противном случае производят расчет деформаций как для железобетонного элемента без трещин.
Кривизну и продольные деформации железобетонного элемента также определяют по нелинейной деформационной модели исходя из уравнений равновесия внешних и внутренних усилий, действующих в нормальном сечении элемента, гипотезы плоских сечений, диаграмм состояния бетона и арматуры и средних деформаций арматуры между трещинами.
6.5.4 Расчет деформаций железобетонных элементов следует производить с учетом длительности действия нагрузок, устанавливаемых соответствующими нормативными документами.
Кривизну элементов при действии постоянных и длительных нагрузок следует определять по формуле
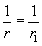, (6.7)
а кривизну при действии постоянных, длительных и кратковременных нагрузок - по формуле
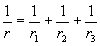, (6.8)
где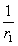 
- кривизна элемента от продолжительного действия постоянных и временных длительных нагрузок;
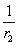- кривизна элемента от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;
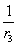- кривизна элемента от непродолжительного действия постоянных и временных длительных нагрузок.
6.5.5 Предельно допустимые прогибы fult определяют по соответствующим нормативным документам (СНиП 2.01.07). При действии постоянных и временных длительных и кратковременных нагрузок прогиб железобетонных элементов во всех случаях не должен превышать 1/150 пролета и 1/75 вылета консоли.
КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
Общие положения
7.1.1 Для обеспечения безопасности и эксплуатационной пригодности бетонных и железобетонных конструкций помимо требований к расчету следует также выполнять конструктивные требования к геометрическим размерам и армированию.
Конструктивные требования устанавливают для тех случаев, когда:
расчетом не представляется возможным достаточно точно и определенно полностью гарантировать сопротивление конструкции внешним нагрузкам и воздействиям;
конструктивные требования определяют граничные условия, в пределах которых могут быть использованы принятые расчетные положения;
конструктивные требования обеспечивают выполнение технологии изготовления бетонных и железобетонных конструкций.
