Сторона эквивалентного прямоугольного сечения:
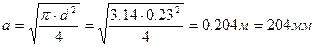
Исходные данные:
, 
, 
, 
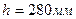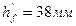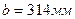1) Определим площадь приведенного сечения.
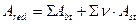
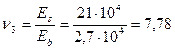
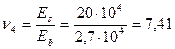
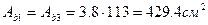
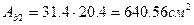
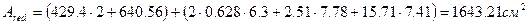
2) Определим статический момент площади приведенного сечения в оси проходящей по грани ребра:
; 
; 
;
; 
; 
; 
;
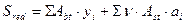
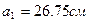Рис. 8 «Расчётное сечение панели для расчёта по второй группе предельных состояний»
3) Расстояние от нижней грани до центра тяжести приведенного сечения.
4) Момент инерции приведенного сечения.
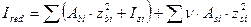
| zb1=13.38-26,1=12.72см zb2=13.38-14=0.62см zb3=13.38-1,9=11,48см | zs1=13.38-26,75=13.37см zs2=13.38-24.5=11.12см zs3=13.38-1,25=12.13см zs4=13.38-3.5=9.88см |
; 
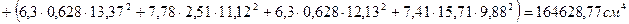
5) Момент сопротивления приведенного сечения.
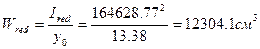
2.10. Расчёт панели по деформациям.
Прогибы продольных ребер считаем по формулам строительной механики, определяем в них значение кривизны по СНИП «Бетонные и железобетонные конструкции».
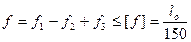- непродолжительная величина прогиба.
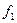- прогиб от непродолжительного действия полной нормативной нагрузки,
- прогиб от непродолжительного действия длительной нагрузки,
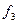- прогиб от продолжительного действия длительной нагрузки.
, где 
- коэффициент, учитывающий схему загружения,
- соответствующая кривизна элемента.
Где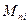 
- соответствующий момент,
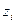- соответствующее плечо пары сил,
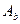- приведенная площадь сжатой зоны бетона над трещиной,
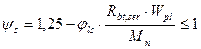-коэффициент, учитывающий работу растянутого бетона на участке между трещинами,
- при непродолжительном действии нагрузки,
- при продолжительном действии нагрузки,
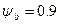- коэффициент, учитывающий влияние сжатых полок,
- коэффициент, учитывающий длительность действия нагрузки,
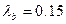- при продолжительном действии нагрузки,
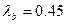- при непродолжительном действии нагрузки.
f1 – прогиб от кратковременного действия всей нагрузки
1) Изгибающий момент Ммах =68,33 кН·м
2) Упругопластический момент сопротивления по растянутой зоне:
Где γ = 1,25 – для двутаврового сечения.
3) Определим величину коэффициента 
, учитывающий неравномерность деформаций в растянутой зоне участка между трещинами:
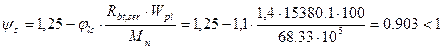
тогда принимаем 
4) Определим величину относительного момента:
5) Определим относительную высоту сжатой зоны:
здесь Т для двутаврового сечения равно:
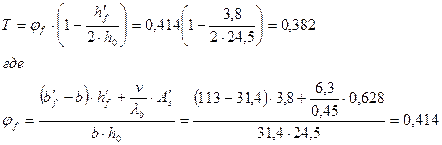
6) Определим положение нейтральной оси и плечо внутренней пары сил z1:
следовательно нейтральная ось проходит в ребре. Тогда
7) Определим кривизну:
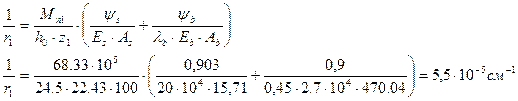
где
Аb – приведенная площадь сжатой зоны бетона над трещиной, см2.
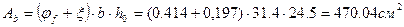
8) Определим прогиб:
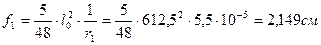
f2 – прогиб от кратковременного действия постоянной и длительной части временной нагрузки.
1) Изгибающий момент Ммах =60,38 кН·м
2) Определим величину коэффициента , учитывающий неравномерность деформаций в растянутой зоне участка между трещинами:
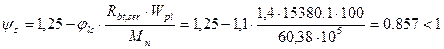
тогда принимаем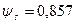 
3) Определим кривизну:
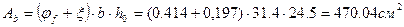
4) Определим прогиб:
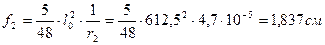
f3 – прогиб от действия постоянной и длительно действующей части временной нагрузки.
1) Изгибающий момент Ммах =60,38 кН·м
2) Определим величину коэффициента , учитывающий неравномерность деформаций в растянутой зоне участка между трещинами:
тогда принимаем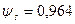 
3) Определим кривизну:
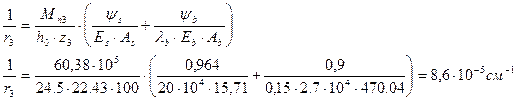
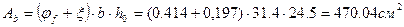
4) Определим прогиб:
Полный прогиб f.
- условие выполняется.
