Введение
Для осуществления когерентного взаимодействия пересекающихся световых пучков с широким спектром слои когерентности одного пучка должны быть параллельны слоям когерентности другого. Для выполнения этого требования при реализации нелинейного взаимодействия могут быть использованы диспергированные световые пучки, в которых слои когерентности не перпендикулярны осям пучков. Изучение характеристик диспергированных пучков производится путем численного моделирования.
Целью работы 7 семестра являлся разбор теории к поставленной задаче, ознакомление с тем, как происходит расчет и построение двумерных распределений модуля и аргумента функции взаимной когерентности, а также ознакомление с методами оптимизации программы.
Аналитические выражения для функции пространственной когерентности пересекающихся пучков
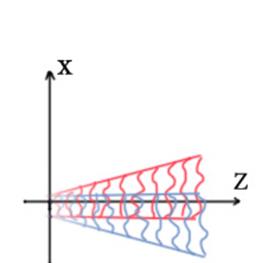
Пара диспергированных лазерных пучков, являющиеся объектом исследования в данном отчете, формируются следующим заданием полей пучков 
и 
,
где 
- перпендикулярная к оси z составляющая волнового вектора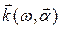 
, 
, n – показатель преломления. Каждый из них наклонен вдоль относительно оси Y Z на угол +χ и –χ, где 
.
Функция взаимной пространственной когерентности широкополосных полей 
и 
определяется выражением
, (1)
где черта означает усреднение во времени. Она определяет интенсивность излучения в области наложения двух широкополосных полей
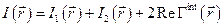, (2)
где 
- интенсивность каждого из полей. где
Функцию 
можно представить в виде
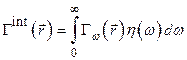, (3)
где
, (4)
. (5)
Целью работы в данном семестре являлось ознакомление с программой расчета 
, проведение предварительного расчета и усовершенствование программы расчета.
Описание предварительного расчета
Численный расчет начинается с расчета полей монохроматических компонент 
. Набор комплексных амплитуд 
, определяющий реализацию пространственного распределения поля в начальной плоскости 
, задается с помощью генератора случайных чисел. Расчет производится в плоскости x, y, перпендикулярной направлению оси z. Значения z = const выбираются вблизи исходной плоскости, в которой z =0, а именно z = 1 см и на некотором удалении от нее с тем, чтобы можно было проследить изменение функции взаимной когерентности по мере распространения пучков. В выбранной области значений x 1 < x < x 2, y 1< y < y 2 фиксируется значение y1, рассчитывается 
, затем 
рассчитывается для следующего значения y 2 и так далее. В конечном итоге мы получаем столбцы значений функции взаимной когерентности 
для всех значений x и y в выбранной области. Компонуя столбцы в матрицу, получаем сечение интерференционной картины, перпендикулярное оси z.
На основе нескольких сечений можно наблюдать динамику пространственного распределение интенсивностей интерферирующих пучков на протяжении оси z с целью дальнейшего изучения их поведения, в том числе при разной ширине спектра.
