Вопросы к экзамену
Первый семестр
1. Определители, их свойства.
2. Матрицы и операции над ними.
3. Обратная матрица.
4. Решение матричных уравнений и линейных систем матричным способом и методом Крамера.
5. Ранг матрицы.
6. Решение систем линейных алгебраических уравнений методом Гаусса.
7. Исследование произвольных систем линейных уравнений. Теорема Кронекера-Капелли..
8. Прямая на плоскости.
9. Кривые второго порядка.
10. Прямая и плоскость в пространстве.
11. Числовая последовательность и ее предел.
12. Предел функции в точке.
13. Непрерывность функции в точке и ее свойства.
14. Точки разрыва и их классификация. Свойства функций, непрерывных на отрезке.
15. Производная функции, ее геометрический и механический смысл. Производные основных элементарных функций. Основные правила дифференцирования функций.
16. Дифференциал функции в точке и его свойства. Применение дифференциала в приближенных вычислениях.
17. Правило Лопиталя.
18. Исследование функции и построение графика.
Образцы заданий к экзамену группы 16ЭД
А=  ; В=
; В=  С=
С= 
D=  ; Е=
; Е= 
1. Выполнить операции над матрицами:

- А*В
-

-

-
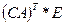
2.Найти  обратную матрицу
обратную матрицу  и сделать проверку.
и сделать проверку.
3. Решить матричное уравнение и сделать проверку.
А*Х= D
4.Вычислить определитель матрицы А по правилу треугольников
5.Вычислить определители при помощи разложения по любой строке или столбцу:
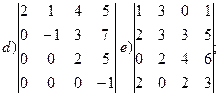
6. Вычислить определитель, упростив его элементарными преобразованиями
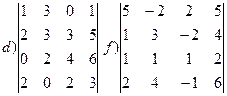
7.Определите ранг следующих матриц:

8. Решить системы уравнений матричным методом и по формулам Крамера.


9.Решить системы уравнений методом Гаусса.

9. г Вычислите объем тетраэдра с вершинами в точках A, B, C, D.
A (14;4;5), B (–5;–3;2), C (–2;–6;–3), D (–2;2;–1).
Составить уравнение плоскости проходящей через точки А,В и С
Составить уравнение прямой ВС
Найти площадь треугольника АВС.
Найти уравнение плоскости, проходящей через точку А перпендикулярно вектору ВС
Установить взаймное положение векторов АВ и СД
Составить уравнение плоскости ВСД и найти угол между плоскостями АВС и ВСД
Найти расстояние от точки D до плоскости АВС
Составить уравнение прямой, проходящей через точку А параллельно вектору ВС
10.г Даны вершины треугольника на плоскости А(2;1) В(4.-3) и С(1;7)
Найти уравнения сторон треугольника.
Найти уравнение высоты, проведенной из вершины В к стороне АС.
Найти площадь треугольника.
Найти расстояние от точки В до прямой АС.
Найти угол между сторонами АВ и АС.
10. Вычислить следующие пределы:
1. 
2. 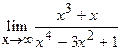
3. 
4. 
5. 
6. 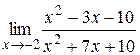
7. 
8. 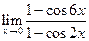
10. 
11. 
12. 
13. 
14. 
11.Найти производные функций и вычислить их значение при х=х0:
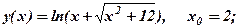

12. Найти производные функций



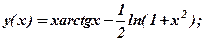
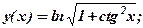
13. Вычислить пределы, используя правило Лопиталя – Бернулли раскрытия неопределенностейвида 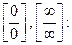


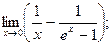
14. Исследовать на монотонность и найти экстремумы функции
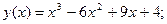

15. Найти наибольшее и наименьшее значения функции на указанном интервале

16.Найти точки перегиба и интервалы выпуклости функции

17. Найти асимптоты графика функции







