Удаление узлов из AVL-деревьев осуществляется по тем же правилам, что и для обычных бинарных упорядоченных деревьев. Однако после этого необходимо проверить баланс дерева. Если найдется узел, где не выполняется свойство AVL-деревьев, необходимо осуществить соответствующее вращение, чтобы перебалансировать дерево.
Красно-черные деревья [12]
Красно-черные деревья – еще один из способов балансировки деревьев. Название происходит от стандартной раскраски узлов таких деревьев в красный и черный цвета. Цвета узлов используются при балансировке дерева. Во время операций вставки и удаления поддеревья может понадобиться повернуть, чтобы достигнуть сбалансированности дерева.
Красно-черное дерево -это бинарное дерево со следующими свойствами:
1. Каждый узел дерева покрашен либо в черный, либо в красный цвет.
2. Листьями объявляются nil-узлы (т.е. "виртуальные" узлы, наследники узлов, которые обычно называют листьями; на них "указывают" nil указатели). Листья покрашены в черный цвет.
3. Если узел красный, то оба его потомка черны.
4. На всех ветвях дерева, ведущих от его корня к листьям, число черных узлов одинаково.
Количество черных узлов на ветви от корня до листа называется черной высотой дерева. Перечисленные свойства гарантируют, что самая длинная ветвь от корня к листу не более чем вдвое длиннее любой другой ветви от корня к листу.
Все вышеперечисленные свойства должны сохраняться при вставке элементов в дерево и удалении из него.
Вставка
Чтобы вставить узел, необходимо сначала найти соответствующее место в дереве. Новый узел всегда добавляется как лист, поэтому оба его потомка являются NIL-узлами и предполагаются черными. После вставки необходимо окрасить узел в красный цвет. После этого необходимо проверить все вышеприведенные свойства для его предка. Далее в случае необходимости осуществляется перекрашивание узла и/или поворот, чтобы сбалансировать дерево.
Вставив красный узел с двумя NIL-потомками, свойство черной высоты (свойство 4) сохранится. Однако при этом может оказаться нарушенным свойство 3, согласно которому оба потомка красного узла обязательно черны. В нашем случае оба потомка нового узла черны по определению (поскольку они являются NIL-узлами), так что необходимо рассмотреть ситуацию, когда предок нового узла красный: при этом будет нарушено свойство 3. Достаточно рассмотреть следующие два случая:
Красный предок, красный "дядя". Данную ситуацию иллюстрирует рис. 17. У нового узла X предок и "дядя" оказались красными. В данном случае простое перекрашивание избавляет от нарушения свойства 3. После перекраски нужно проверить "дедушку" нового узла (узел B), поскольку он может оказаться красным. Следует обратить внимание на то, что в данном случае меняется цвет корня дерева, т.к. в противном случае нарушилось бы свойство черной высоты.
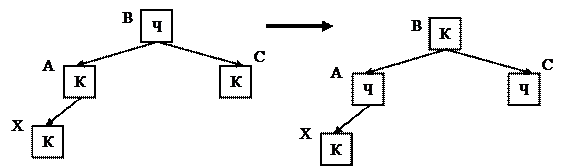 |
Рис. 17. Вставка – Красный предок, красный дядя
Красный предок, черный "дядя". На рис. 18 представлен другой пример нарушения свойства 3 красно-черных деревьев. В данном случае для коррекции необходимо применить дополнительно вращение узлов. Следует обратить внимание, что если узел X был в начале правым потомком, то для коррекции следует применять левое вращение, которое делает этот узел левым потомком.
 |
Рис. 18. Вставка – красный предок, черный дядя
Деревья со случайным поиском [13]
При вводе элемента в дерево случайного поиска этому элементу присваивается приоритет - некоторое вещественное число с равномерным распределением в диапазоне [0, 1]. Приоритеты элементов в дереве случайного поиска определяют их положение в дереве в соответствии с правилом: приоритет каждого элемента в дереве не должен быть больше приоритета любого из его последователей. Правило двоичного дерева поиска также остается справедливым: для каждого элемента х элементы в левом поддереве должны быть меньше, чем х, а в правом - больше, чем х. На рис. 19 приведен пример такого дерева случайного поиска, на котором приоритеты каждого элемента указаны в виде нижнего индекса.
 |
Рис. 19. Дерево случайного поиска. Приоритеты каждого элемента указаны в виде нижнего индекса
Ввод элемента х в дерево случайного поиска выполняется в два этапа. На первом этапе необходимо определить позицию узла в дереве в соответствии с правилами обычного бинарного упорядоченного дерева. На втором этапе необходимо изменить форму дерева в соответствии с приоритетами элементов. В этом случае может потребоваться либо правое, либо левое вращение.
Б-деревья [14]
Б-деревья (B-tree) [15] - другая форма сбалансированного дерева. Каждый узел в Б-дереве содержит ключи и несколько указателей на дочерние узлы. Поскольку каждый узел хранит несколько элементов, узлы часто называются сегментами. Между каждой парой смежных указателей в узле находится ключ, который используется для определения ветви, по которой нужно двигаться при добавлении или поиске элемента. На рис. 20 изображено Б-дерево, содержащее два ключа – G и R.
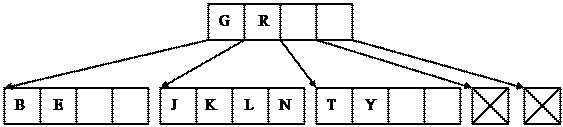 |
Рис. 20. Б-дерево
Чтобы разместить элемент со значением меньшим G, нужно следовать вниз по первой ветви. Чтобы найти значение между G и R, необходимо пройти вниз по второй ветви. Разместить элемент со значением большим R можно, выбрав третью ветвь.
Б-дерево порядка К обладает следующими свойствами:
· каждый узел содержит максимум 2К ключей;
· каждый узел, за исключением корня, содержит не менее К ключей;
· внутренний узел, где расположено М ключей, имеет М + 1 дочерних узлов;
· все листья дерева находятся на одном уровне.
Б-дерево на рис. 20 имеет порядок 2. Каждый узел может содержать до четырех ключей. Каждый узел, кроме корня, должен содержать не менее двух ключей.
Требование, чтобы каждый узел в Б-дереве порядка К содержал от К до 2К ключей, поддерживает баланс дерева. Поскольку каждый узел должен содержать, по крайней мере, К ключей, он должен иметь не меньше К+1 дочерних узлов, поэтому дерево не может стать слишком высоким и тонким.






