Методические указания к решению задач контрольной работы.

Задания к контрольной работе

И методические указания к их выполнению

Математическая статистика (математика и статистика).

 

Задание 1. Из букв разрезной азбуки составлено некоторое слово. Карточки перемешаны и разложены в случайном порядке. Найти вероятность того, что получится первоначальное слово.

1.1 АСТРА 1.2 МОЛОКО 1.3 СЛАВА 1.4 ЗОЛОТО 1.5 СУММА 1.6 ТЕРЕМ

1.7 ЛАГУНА 1.8 ССЫЛКА 1.9 ФИНИК 1.10 АЛМАЗ

Задание 2. В партии из n изделий m бракованных. Из партии для контроля выбирают k изделий. Найти вероятность того, что все выбранные изделия не бракованные.

2.1 n=30, m=5, k=4. 2.2 n=25, m=3, k=5.

2.3 n=20, m=2, k=3. 2.4 n=30, m=4, k=5.

2.5 n=20, m=4, k=5. 2.6 n=35, m=6, k=5.

2.7 n=25, m=4, k=2. 2.8 n=24, m=4, k=3.

2.9 n=30, m=6, k=3. 2.10 n=26, m=3, k=4.

 

Задание 3. Два стрелка стреляют одновременно в мишень. Первый стрелок попадает с вероятностью р₁, второй стрелок – с вероятностью р₂. Найти вероятности следующих событий: 1) оба стрелка попадут в мишень; 2) только один из стрелков попадет в мишень.

3.1 р₁ = 0.7, р₂ = 0.6. 3.2 р₁ = 0.8, р₂ = 0.5. 3.3 р₁ = 0.7, р₂ = 0.8. 3.4 р₁ = 0.6, р₂ = 0.8.

3.5 р₁ = 0.9, р₂ = 0.6. 3.6 р₁ = 0.7, р₂ = 0.9. 3.7 р₁ = 0.5, р₂ = 0.6. 3.8 р₁ = 0.8, р₂ = 0.9.

3.9 р₁ = 0.7, р₂ = 0.5. 3.10 р₁ = 0.8, р₂ = 0.4.

 

Задание 4. В первой урне n₁ белых и n₂ черных шаров, а во второй урне m₁ белых и m₂ черных шаров. Из каждой урны удалили по одному шару, а оставшиеся шары ссыпали в третью урну. Найти вероятность того, что случайно выбранный из третьей урны шар окажется белым.

4.1 n₁=2, n₂=8, m₁=5, m₂=3. 4.2 n₁=4, n₂=6, m₁=3, m₂=7.

4.3 n₁=5, n₂=5, m₁=4, m₂=6. 4.4 n₁=7, n₂=3, m₁=6, m₂=2.

4.5 n₁=6, n₂=4, m₁=5, m₂=4. 4.6 n₁=3, n₂=7, m₁=4, m₂=4.

4.7 n₁=8, n₂=2, m₁=2, m₂=6. 4.8 n₁=1, n₂=9, m₁=5, m₂=5.

4.9 n₁=2, n₂=8, m₁=2, m₂=4. 4.10 n₁=5, n₂=6, m₁=2, m₂=8.

 

Задание 5. Купленоn билетов лотереи, вероятность выигрыша одного билета равна p. Найти наивероятнейшее число выигравших билетов и вероятность этого числа.

5.1 n= 12, p = 0.2 5.2 n= 10, p = 0.3 5.3 n= 10, p = 0.1 5.4 n= 8, p = 0.2

5.5 n= 15, p = 0.3 5.6 n= 12, p = 0.1 5.7 n= 10, p = 0.2 5.8 n= 15, p = 0.1

5.9 n= 14, p = 0.2 5.10 n= 12, p = 0.3

 

Задание 6. По выборке объема n=50 составлен вариационный ряд. Найти: а) частоту n₃; б) среднюю выборочную ; в) исправленную дисперсию ; г) стандартное отклонение 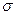; д) начертить полигон частот.

 

xi
ni			n3

6.1

xi	-1
ni			n3

6.2

 

 

xi	-6	-3	-2
ni			n3

6.3

 

 

xi
ni			n3

6.4

 

 

xi	-4	-2	-1
ni			n3

6.5

 

 

xi	-2
ni			n3

 

6.6

 

xi	-10	-5	-3
ni			n3

6.7

 

 

xi
ni			n3

6.8

 

xi	-1
ni			n3

6.9

 

 

xi	-7	-3	-1
ni			n3

6.10

 

Методические указания к решению задач контрольной работы.

Задание 1. Из букв разрезной азбуки составлено слово ХОРОШО. Карточки перемешаны и разложены в случайном порядке. Найти вероятность того, что получится первоначальное слово.

 

Решение. Обозначим: событие А – «получится первоначальное слово ХОРОШО». Вероятность этого события вычислим по формуле классической вероятности: где N – количество всех возможных исходов опыта, а M – количество исходов опыта, благоприятствующих событию А.

 

В слове 6 букв, поэтому количество всех возможных «слов» равно: N = P ₆ = 6! = 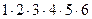=720

В слове 3 буквы О, от их перестановки слово не изменится, поэтому количество исходов опыта, благоприятствующих событию А: М = Р ₃ = = 6.

 

Задание 2. В партии из 30 изделий 2 бракованных. Из партии для контроля выбирают 6 изделий. Найти вероятность того, что все выбранные изделия не бракованные.

 

Решение. Обозначим событие А – «все выбранные изделия не бракованные». Вероятность этого события вычислим по формуле классической вероятности: где N – количество всех возможных исходов опыта, а M – количество исходов опыта, благоприятствующих событию А.

Количество не бракованных изделий равно: 20 – 2 = 18. Тогда:

 

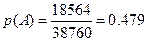
Задание 3. Два стрелка стреляют одновременно в мишень. Первый стрелок попадает с вероятностью 0.9, второй стрелок – с вероятностью 0.5. Найти вероятности следующих событий: 1) оба стрелка попадут в мишень; 2) только один из стрелков попадет в мишень.

 

Решение. Обозначим события:

А – «первый стрелок попал», по условию р(А)=0.9

В – «второй стрелок попал», по условию р(В)=0.5

С – «оба стрелка попадут», С =

D – «только один из стрелков попадет», D = . Тогда:

р(А) = р(А) р(В) = = 0.45;

р(D) = = = = 0.50

 

Задание 4. В первой урне 5 белых и 3 черных шара, а во второй урне 6 белых и 4 черных шара. Из каждой урны удалили по одному шару, а оставшиеся шары ссыпали в третью урну. Найти вероятность того, что случайно выбранный из третьей урны шар окажется белым.

 

Решение. В этой задаче опыт производится в два этапа: сначала шары удаляются из урн и ссыпаются в третью урну, а потом из третьей урны берется один шар. Такие задачи решают с помощью формулы полной вероятности:

В 1-ой урне 5 + 3 = 8 шаров; во 2-й: 6 + 4 = 10 шаров.

1) Сформулируем гипотезы:

Н₁: из 1-ой урны удалили белый шар, из 2-ой – белый;

Н₂: из 1-ой урны удалили белый шар, из 2-ой – черный;

Н₃: из 1-ой урны удалили черный шар, из 2-ой – белый;

Н₄: из 1-ой урны удалили черный шар, из 1-ой – черный;

 

 

Проверка: .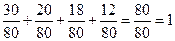

2) Событие А – из 3-й урны взят белый шар. В 1-ой урне осталось 8 – 1 = 7 шаров, во 2-ой: 10 – 1 =9 шаров. В 3-ю урну ссыпали 7+9 = 16 шаров. Найдем условные вероятности:

; .

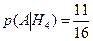По формуле полной вероятности:

 

Задание 5. Куплено15 билетов лотереи, вероятность выигрыша одного билета равна 0.2. Найти наивероятнейшее число выигравших билетов и вероятность этого числа.

 

Решение. Рассмотрим схему Бернулли, n= 15, p = 0.2, q = 1 - p = 1 - 0.2 = 0.8;

наивероятнейшее число m выигравших билетов находится по формуле:

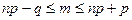
; ; m = 3.

Вероятность этого числа находим по формуле Бернулли:

Подставим в формулу данные, получим:

=

 

Задание 6. По выборке объема n=50 составлен вариационный ряд. Найти: а) частоту n₃; б) среднюю выборочную ; в) исправленную дисперсию ; г) стандартное отклонение 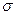; д) начертить полигон частот.

xi
ni			n3

 

Решение. а). Сумма всех частот равна объему выборки: , тогда 50 = 11 + 9+ n₃+ 12+10, поэтому

n₃= 50 - (11+9+12+10) = 8;

б) = =1.2

в) исправленная дисперсия: ;

S² =15.71

г) стандартное отклонение 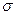находится по формуле: = =

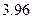
д) начертить полигон частот.

 

Литература

 

1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа. 2000. 400с.
2. Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика. /Учебное пособие. М.: Гароарика, 1998. 326с.