
Преобразованная система имеет вид



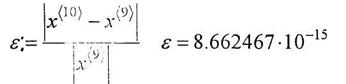
Указание: Для проверки выполнения достаточного условия сходимости метода можно ограничиться любой из вышеперечисленных норм. Для реализации итерационных вычислений с векторами в Mathcad удобно использовать описание вектора-столбца прямоугольной матрицы. В качестве нулевого приближения выбран вектор правых частей преобразованной системы. Затем вычислены 10 приближений решения, которые сохраняются в матрице х так, что k-е приближение хранится в ее k-том столбце. Для того, чтобы вывес-
ти на экран все найденные приближения, с клавиатура нужно ввести имя матрицы решений х и знак равенства. При выводе на экран больших матриц автоматически откр ывает ся
окно с полосой прокрутки. Чтобы вычислить норму вектора щелкните по кнопке \х\ в панели матричных инструментов и введите в помеченной позиции имя вектора.
1.5. Общая теория линейных систем.
Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно п неизвестных Х 1, Х2,..., Хп

Для такой системы справедлива теорема Кронекера – Капелли; для того, чтобы неоднородная система линейных алгебраических уравнений была совместна (система совместна если она имеет хотя бы одно решение), необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Исследовать неоднородную систему - значит установить, является ли она совместной и, если является - найти выражение для общего решения системы.
Применим для исследования метод Гаусса.

расширенная матрица исследуемой системы, ранг которой r равен рангу матрицы системы и r<п Такая матрица методом Гаусса сводится к ступенчатому виду.

Получим систему

Затем из данной системы выразим базисные переменные x1,х2,...,хn через свободные переменные xr+1,xr+2,...,xn.

Эти уравнения выражают общее решение системы. Положив свободные переменные равными 0,  вычисляем базисные переменные и получаем частное решение исследуемой системы:
вычисляем базисные переменные и получаем частное решение исследуемой системы:

Пример исследования неоднородной системы алгебраических
Уравнений.

Cистема совместна.
Приведем матрицу к ступенчатой форме:

Свободные переменные: х4, х5, базисные - xl, х2, хЗ. Запишем, и решим эквивалентную систему:


Общее решение Частные решения

- Порядок выполнения работы
2.1 Нахождение методом Гаусса решения системы линейных алгебраических уравнений.
1. Запустить программу Mathcad
2. Установить режим автоматических вычислений
3. Присвоить переменной ORIGIN значение, равное 1
4. Ввести матрицу системы и матрицу - столбец правых частей.
5. Сформировать расширенную матрицу системы.
6. Привести расширенную матрицу системы к ступенчатому виду.
7. Сформировать столбец решения системы.
8. Проверить правильность решения умножением матрицы системы на вектор-столбец решения.
2.2.Нахожденпе методом простых итераций приближенное решение линейной системы.
1. Запустить программу Mathcad.
2. Установить режим автоматических вычислений.
3. Преобразовать исходную систему Сх = d к виду х = b + Ах.
4. Ввести матрицы А и Ь.
5. Проверить достаточное условие сходимости.
6. Определить. нулевое (начальное) приближение решения.
7. Задать количество итераций.
8. Ввести формулу вычисления последовательных приближений решения и вычислить их.
9. Вывести на. экран матрицу приближенных решений.
10. Вычислить погрешность найденного приближения.
2.3.Исследовать однородную систему линейных алгебраических уравнений:
1. Установить режим автоматических вычислений.
2. Ввести матрицу системы и расширенную матрицу системы.
3. Вычислить ранг основной матрицы и ранг расширенной системы.
4. Сформулировать и записать в рабочем документе соответствующий вывод.
5. Если система совместна, привести расширенную матрицу этой системы к ступенчатому виду.
6. Определить базисные и свободные элементы.
7. Записать эквивалентную систему и разрешить ее относительно базисных переменных.
8. Записать общее решение системы.
9. Найти два различных частных решения.
- Содержание отчета:
3.1. Наименование работы.
3.2. Цель работы.
3.3. Решение данной системы методом Гаусса. (Приложение 1)
3.4. Решение данной системы методом простых итераций. (Приложение 1)
3.5. Исследование данной неоднородной системы. (Приложение 2)
- Контрольные вопросы
1. В чем состоит прямой и обратный ход метода Гаусса?
2. Какая функция выполняет в Mathcad прямой и обратный ход метода Гаусса?
3. В каких случаях применяют итерационные методы для решения систем уравнений?
4. Как вводится понятие нормы матрицы, согласованной с нормой вектора?
5. К какому виду нужно привести исходную систему уравнений, прежде чем применить метод простых итераций.
6. В каком случае система будет являться несовместной?
Литература:
- Просветов Г.И. Математические методы и модели в экономике. «Альфа-Пресс», М.; 2008
- Мелкумов Я.С. Финансовые вычисления. Теория и практика. «Инфра – М», М.; 2007
Приложение №1


Приложение №2





