Лабораторная работа №3
«Нахождение собственных чисел и собственных векторов матрицы»
Теоретический материал
1. Метод Крылова. Собственные числа матрицы А определяют путём решения характеристического уравнения, приведённого к виду

Значение  являются решениями системы, полученной из векторного равенства
являются решениями системы, полученной из векторного равенства
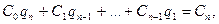
где  – начальный вектор (произвольный),
– начальный вектор (произвольный),  . Решая эту систему, например при помощи метода Гаусса, находят
. Решая эту систему, например при помощи метода Гаусса, находят  .
.
Собственные векторы матрицы А определяют из соотношения
 (i =1,2,…, n)
(i =1,2,…, n)
где  – коэффициенты частного, полученного при делении
– коэффициенты частного, полученного при делении  на
на 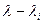 .
.
Пример решения задачи методом Крылова
A = 

1. Для определения коэффициентов характеристического уравнения
l4 – p1 l3 – p2 l2 – p3 l – p4 = 0
строим последовательность векторов:
В0 ¾ произвольный вектор; В1 = АВ0; В2 = АВ1; В3 = АВ2; В4 = АВ3.
Если векторы В0, В1, В2, В3 окажутся линейно независимыми, то коэффициенты p1, p2, p3, p4 определяются из решения системы линейных уравнений, соответствующей равенству
В4 = p1 В3 + p2 В2 + p3 В1 + p4 В0.
Систему линейных уравнений решаем средствами Excel или MathCAD, можно воспользоваться также программной реализацией метода Гаусса из лабораторной работы №1.
Таблица 1
| А | В0 | В1 | В2 | В3 | В4 | |||
| 2,2 | 0,5 | 2,2 | 10,09 | 52,373 | 291,0006 | |||
| 1,3 | 6,5 | 41,84 | 239,605 | |||||
| 0,5 | 0,5 | 1,6 | 0,5 | 6,55 | 37,64 | 220,7825 | ||
| 1,6 | 10,20 | 57,56 | 321,930 |
Таким образом, характеристическое уравнение матрицы имеет вид
 . (*)
. (*)
2. Определение собственных чисел матрицы состоит в решении полученного характеристического уравнения (*), например, средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2.
Собственные числа матрицы А таковы:
l1 = 5,652; l2 = 1,545; l3 = –1,420; l4 = 0,2226.
3. Собственный вектор X i, соответствующий собственному числу l i, определяется по формуле
X i= b i 3B0 + b i 2B1 + b i 1B2 + b i 0B3,
где коэффициенты при ранее найденных векторах В0, В1, В2, В3 находятся из равенства
 = b i 0l3 + b i 1l2 + b i 2 + b i 3.
= b i 0l3 + b i 1l2 + b i 2 + b i 3.
Окончательные значения собственных векторов должны иметь кубическую норму, равную единице. Для того, чтобы собственный вектор имел кубическую норму, равную единице, нужно разделить все компоненты вектора на максимальную по модулю компоненту.
Все вычисления приведены в таблице 2.
Таблица 2
| l i | b i 3B0 | b i 2B1 | b i 1B2 | b i 0B3 | X i | 
|
| 5,652 | 0,4877 | –4,7672 –2,1669 –1,0334 –4,3338 | –3,5113 –2,2620 –2,2794 –3,5496 | 52,373 41,84 37,64 57,56 | 44,5822 37,4111 34,2772 49,6766 | 0,879 0,753 0,690 1,0 |
| 1,545 | 1,7918 | –15,5826 –7,08298 –3,5415 –14,1660 | –44,9510 –28,9575 –29,1802 –45,4410 | 52,373 41,84 37,64 57,56 | –6,3688 5,7995 4,9183 –2,0470 | –0,911 –0,772 0,321 |
| –1,420 | –1,9427 | 22,7400 10,3364 5,1682 20,6728 | –74,8678 –48,2300 –48,6010 –75,6840 | 52,373 41,84 37,64 57,56 | –1,6975 3,9464 –5,7928 2,5488 | 0,293 –0,681 –0,440 |
| 0,2226 | 12,4042 | –5,2692 –1,4860 –0,7430 –2,9720 | –58,2940 –37,5531 –37,8420 –58,9295 | 52,373 41,84 37,64 57,56 | 3,2140 2,8009 –0,9450 –4,3415 | –0,740 –0,645 –0,218 |
2. Метод Данилевского. Для определения коэффициентов характеристического уравнения матрицу A с помощью n-1 преобразований подобия заменяют подобной ей матрицей Фробениуса
P= 
На первом этапе находят:
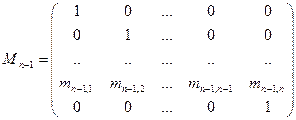
где 


где 


 (матрица С подобна матрице А);
(матрица С подобна матрице А);

где 
Пример решения задачи методом Данилевского
A = 

1. Коэффициенты характеристического уравнения матрицы А определяются как элементы первой строки матрицы Фробениуса Р, подобной данной матрице А. Матрицу Р найдем в результате трех преобразований подобия:
Р = М-11× М-12× М-13×АМ3×М2×М1.
Округляя значения коэффициентов до четырех десятичных знаков, получим характеристическое уравнение
l4 – 6l3 – 0,2l2 + 12,735l – 2,7616 = 0.
Это уравнение решаем средствами Excel или MathCAD, можно использовать программную реализацию одного из методов лабораторной работы №2. Корни уравнения таковы:
l1 = 5,652; l2 = 1,545; l3 = –1,420; l4 = 0,2226.
2. Собственный вектор X i, соответствующий собственному числу l i, определяется равенством
X i = М3 ×М2× М1×Y i, где Y i = 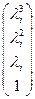 .
.
Результаты вычисления собственных векторов приведены в таблице 3.
Таблица 3
| li | M1 | M2 | M3 | Yi | Xi | 
|
| 5,652 | –0,231125 1,078582 1,651001 1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 180,5537 31,9451 5,652 | 0,8977 0,7529 0,6898 | 0,898 0,753 0,690 |
| 1,545 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 3,6880 2,3870 1,545 | 3,1143 –2,8359 –2,4048 | –0,911 –0,772 –0,440 |
| 0,2226 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | 0,01103 0,4955 0,2226 | –0,7403 –0,6451 0,2177 | –0,740 –0,645 0,218 |
| –1,420 | –0,231125 1,078582 1,651001 –1,158706 | –0,351515 0,242424 –1,060606 –0,681212 | –1,25 –0,625 0,625 –1,25 | –2,8633 2,0164 –1,420 | –0,6665 1,5480 –2,2719 | 0,293 –0,681 –0,440 |
3. Метод итераций для определения первого собственного значения и соответствующего ему собственного вектора матрицы А. Строят последовательность векторов: 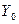 – произвольный вектор,
– произвольный вектор,  . Тогда
. Тогда
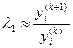
где 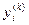 и
и  – одноименные координаты двух последовательных векторов;
– одноименные координаты двух последовательных векторов;
При этом собственный вектор  .
.
Пример решения задачи методом итераций
1. Строим последовательность векторов  , где
, где  - произвольный вектор; тогда
- произвольный вектор; тогда  , где
, где 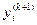 и
и  – одноименные координаты двух последовательных векторов.
– одноименные координаты двух последовательных векторов.
Все вычисления приведены в таблице 4.
Таблица 4
| 1,6 | 2,3 | 1,2 | ||||
| A | 2,3 | 0,6 | 1,5 | 
| 
| 
|
| 1,2 | 1,5 | 3,8 | ||||

| ||||||

| 5,1 | 4,4 | 6,5 | 5,11 | 5,48 | 5,76 |

| 26,08 | 24,12 | 37,42 | 5,45 | 5,41 | 5,60 |

| 142,108 | 130,586 | 209,672 | 5,484 | 5,511 | 5,548 |

| 
| 
| 
| 5,5151 | 5,5148 | 5,5321 |

| 
| 
| 
| 5,5205 | 5,5225 | 5,5267 |

| 
| 
| 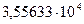
| 5,5233 | 5,5235 | 5,5251 |

| 
| 
| 
| 5,5240 | 5,5241 | 5,5246 |

| 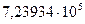
| 
| 
| 5,5242 | 5,5243 | 5,5244 |

| 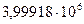
| 
| 
| 5,5243 | 5,5243 | 5,5244 |

| 
| 
| 
| 5,5243 | 5,5243 | 5,5243 |

| 
| 
| 
|
Итак,  .
.
2. Собственный вектор  определяется из равенства
определяется из равенства  . Следовательно,
. Следовательно,  . Для того, чтобы собственный вектор
. Для того, чтобы собственный вектор  имел кубическую норму, равную единице, разделим все компоненты вектора на максимальную по модулю компоненту. Получим
имел кубическую норму, равную единице, разделим все компоненты вектора на максимальную по модулю компоненту. Получим  . Такую нормировку рекомендуется выполнять на каждой итерации для ограничения роста компонент вектора
. Такую нормировку рекомендуется выполнять на каждой итерации для ограничения роста компонент вектора  .
.
Задания лабораторной работы №3
«Нахождение собственных чисел и собственных векторов матрицы»
Задание для нечетных вариантов:
1. Используя метод Крылова найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Крылова средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Крылова можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Крылова и методом итераций.
Задание для четных вариантов:
1. Используя метод Данилевского найти собственные числа и собственные вектора матрицы А. Разрешается реализовывать метод Данилевского средствами MathCAD или Mathematica (корни характеристического уравнения найти с помощью встроенных функций). Метод Данилевского можно реализовать также на VBA (корни характеристического уравнения найти с помощью команды «Поиск решения» или «Подбор параметра» пункта меню Сервис в Excel).
2. Используя метод итераций, определить первое собственное число матрицы (наибольшее по модулю). Найти соответствующий ему собственный вектор, имеющий кубическую норму, равную 1. Метод итераций реализовать на языке программирования.
3. Сравнить результаты, полученные методом Данилевского и методом итераций.
Варианты заданий
№1. A =  №2. А =
№2. А = 
№3. A =  №4. А =
№4. А = 
№5. A =  №6. А =
№6. А = 
№7. A =  №8. А =
№8. А = 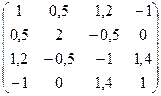
№9. A = 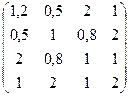 №10. А =
№10. А = 
№11. A = 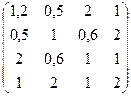 №12. А =
№12. А = 
№13. A =  №14. А =
№14. А = 
№15. A =  №16. А =
№16. А = 
№17. A = 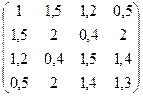 №18.А =
№18.А = 
№19. A = 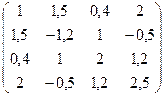 №20.А =
№20.А = 
№21. A =  №22. А =
№22. А = 
№23. A = 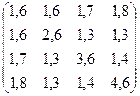 №24. А =
№24. А = 
№25. A = 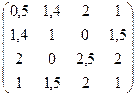 №26. А =
№26. А = 
№27. A = 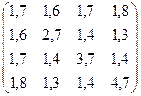 №28. А =
№28. А = 
№29. A =  №30. А =
№30. А = 






