Кафедра прикладной механики

ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

Кафедра прикладной механики

 

 

КУРСОВОЙ ПРОЕКТ

 

по дисциплине: «Теория машин и механизмов»

на тему:

«Исследование рычажных механизмов»

 

Задание № 15- МД- а

 

Работу выполнил: студент гр.МД-09-1_____

Гриднев И.А.__________­­­­­

 

Работу принял: Бондаренко П.А.

_______________________

 

 

Липецк 2011

Здесь вставляется задание и синтез с рисунками!

 

Оглавление

 

1. Структурный анализ механизма……………………………………………..

 

2. Кинематический анализ механизма…………………………………………

 

2.1. План механизма ……………………………………………………..

 

2.2. План скоростей ……………………………………………………...

 

2.3 План ускорений ………………………………………………………

 

3. Кинетостатический анализ ………………………………………………….

 

3.1. Определение инерционных сил ……………………………………

 

3.2. Силовой расчет группы 4-5 …………………...……………………

 

3.3. Силовой расчет группы 3-2 …………………………………………

 

3.4. Силовой расчет входного звена ……………………………………

 

4. «Рычаг» Жуковского ……………………………………………………….

 

 

1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

 

Механизм является плоским и не содержит высших пар 4 класса.

Звенья механизма образуют следующие кинематические пары

 

Кинем. пары	0-1	1-2	2-3	3-0	3-4	4-5	5-0
Вид дв.	В	В	В	П	В	П	П

 

В – вращательная пара

П – поступательная пара

 

Определяем число степеней свободы по формуле Чебышева

 

 

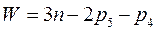
Где n – число подвижных звеньев

р₅ – число пар 5-го класса

р₄ - число пар 4го класса

 

 

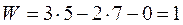
Это означает, что механизм может иметь только одно начальное звено, которое задает положение механизма.

 

Звено 1 вращается, совершая полный оборот, и называется кривошипом.

 

Звено 2 совершает вращательное движение с неполным оборотом и называется шатуном.

 

Звено 3 совершает поступательное движение и называется ползуном

 

Звено 4 совершает сложное движение и совершает не полный оборот. Такое звено называется шатуном.

 

Звено 5 совершает возвратно поступательные движения и называется ползуном.

 

Все кинематические пары 5 класса.

 

 

Разбиваем механизм на группы Асура

 

 

Формула механизма имеет вид

1кл (1-0) → 2кл (2-3) → 2кл (4-5)

Поскольку класс механизма определяется наивысшим классом входящих в механизм, то механизм относиться ко 2 классу.

 

 

2.КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

 

2.1. ПОСТРОЕНИЕ ПЛАНА МЕХАНИЗМА

 

Выбираем масштаб таким образом, чтобы план положения механизма занял примерно 1/5….1/4 часть площади листа формата А1.

 

Где l_АВ – длина звена на чертеже (мм).

АВ – натуральная длина звена (м).

 

Находим остальные длины звеньев на чертеже

 

 

В соответствии с выбранным масштабе определяем длины всех линейных величин и строим план механизма в заданном положении (φ = 45 ⁰). План механизма в заданном положении вычерчиваем основными линиями.

 

2.2. ПОСТРОЕНИЕ ПЛАНА СКОРОСТЕЙ

 

 

По заданной частоте вращения n1 определяем угловую скорость кривошипа

 

Найдем скорость точки B

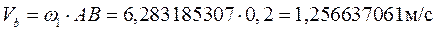
Где АВ – длина кривошипа, м.

Вектор скорости точки B направлен перпендикулярно к кривошипу в сторону его вращения.

 

Из произвольной точки р (полюс плана скоростей) проводим вектор рb, изображающий скорость точки В в масштабе скоростей.

 

Выбираем масштаб плана скоростей

 

Для определения скорости точки С необходимо воспользоваться теоремой о разложении сложного движения

Где - известный по величине и направлению вектор скорости.

- неизвестный по величине вектор абсолютной скорости точки С, направление которого горизонтально.

- неизвестный по величине вектор скорости точки С относительно точки В, направление которого перпендикулярно к СВ.

 

Через конец вектора рb (точка b) проводим прямую, перпендикулярную к CB (направление вектора V cb), а из полюса р – прямую, горизонтальную (направление вектора абсолютной скорости V c). Вектор рc изображает на плане скоростей абсолютную скорость V c, а вектор аb, соединяющий концы векторов абсолютных скоростей, - относительную скорость V cb.

 

Скорости точек А, и опоры равняются нулю, поэтому точка а, на плане скоростей совпадают с полюсом р.

 

Скорости точки С принадлежащие звену 2,звену 4 и звену 3 равны т.к. в этой точке они образуют вращательную пару.

 

Находим модули скоростей

 

Определим скорость точки С принадлежащую звену 5.

 

 

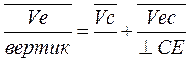
Находим модули скорости скоростей

 

Находим скорости центра масс звеньев

 

Определяем угловые скорости звеньев через линейные скорости

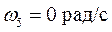т.к. движутся поступательно.

 

Для определения направления угловой скорости мысленно переносим вектор скорости нужного звена в точки ее приложения на плане механизма и смотрим, как будет вращаться звено под действием этого вектора.

 

 

2.3. ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ

 

Так как кривошип вращается равномерно (n=const), ускорение точки В будет равно нормальной его составляющей

 

Ускорение точки В направлено к центру вращения А.

 

Из произвольной точки π (полюс плана ускорений) проводим вектор πb, изображающий на плане ускорение точки В в масштабе плана ускорений.

 

Выбираем масштаб плана ускорений

 

Точка С принадлежит 2 и 3 звену, тогда ускорение точки С

Левая часть – точка С принадлежит 3 звену, а правая часть – 2 звену.

 

Находим длины векторов ускорений на чертеже

 

Теперь решаем наше уравнение графически и находим модули ускорений

 

 

Ускорение точки Е найдем по теореме сложного движения

 

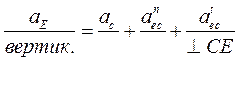
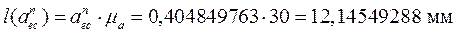
Решаем графически.

 

Находим модули ускорений

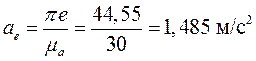
Находим ускорения центра масс

 

 

Находим угловые ускорения звеньев через тенгенсальную составляющую

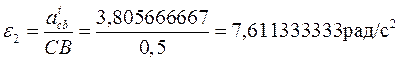
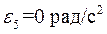движется поступательно

 

Для определения направления угловых ускорений мысленно переносим вектор (тангенсальный) в точку механизма и смотрим, в какую сторону будет вращаться звено под действием этого вектора относительно точки вращения.

 

 

3. КИНКТОСТАТИЧЕСКИЙ АНАЛИЗ

 

3.1. ОПРЕДЕЛЕНИЕ ИНЕРЦИОННЫХ СИЛ

 

Звено 5.

Поскольку звено 5 движется поступательно, ε₅=0 и равнодействующая сил инерции совпадает с их главным вектором:

 

а направление ее противоположено .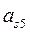

 

Инерционные силы звеньев, массы и моменты которых не заданы, предполагаются пренебрежимо малыми и в силовом расчете не учитываются.

 

 

Определяем по графику силу полезного сопротивления F_пс.

 

 

4.2.СИЛОВОЙ РАСЧЕТ ГРУППЫ 4-5.

 

Отделяем нулевую группы 4-5 от механизма и нагружаем ее силами.

Звенья вычерчиваются в масштабе, векторы сил изображаются произвольными отрезками. Должны быть показаны силы полезных сопротивлений, силы тяжести, силы инерции и силы реакции в отброшенных связях, которые определяются решением уравнении статики.

 

Уравнение статики

 

 

Составим уравнение моментов относительно точки Е для группы 5 – 4, получаем что

 

 

Развернутая запись первого уравнения имеет вид

 

Выбираем масштаб

 

 

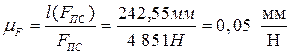
Определяем длины отрезков, выражающие модули сил в масштабе.

 

 

Решаем графически.

Находим модули сил.

 

 

 

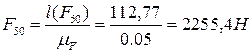
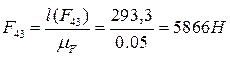
4.3.СИЛОВОЙ РАСЧЕТ ГРУППЫ 3-2

 

Отделяем группу 2-3 от механизма и нагружаем ее силами реакцию в шарнире раскладываем на и .

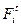Уравнение статики

 

Составим уравнение моментов относительно точки В для 3 – 2. И от сюда найдем силу

 

 

Если в результате расчетов сила получается отрицательной, то это означает, что направление этой силы принятое в начале произвольно, следует изменить на противоположенное направление.

 

 

Развернутый вид первого уравнения имеет вид

 

Определяем масштаб

 

Находим длины отрезков, выражающие модули сил в масштабе.

 

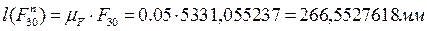
Решаем графически.

 

Определяем модули сил.

 

 

4.4. СИЛОВОЙ РАСЧЕТ ВХОДНОГО ЗВЕНА

 

На входное звено 1 действует известная сила реакции F₁₂ = -F₂₁, неизвестная реакция F₁₀ и уравновешивающий момент М_У. Записываем уравнение равновесия входного звена

 

 

Которые позволяют найти момент который заменяем эквивалентной парой сил и 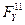, и силу .

 

 

 

5. «РЫЧАГ» ЖУКОВСКОГО

 

Теоретической основой данного метода является известный из курса теоретической механики принцип возможных перемещений. Для механизмов с одной степенью свободы принцип возможных перемещений сводится к равенству мощности приведенной силы (или приведенного момента) к сумме мощностей всех реально приложенных к звеньям механизма сил и моментов сил.

Строим «рычаг» Жуковского, поворачивая план скоростей на 90 градусов.

Прикладываем в соответствующие точки известные силы тяжести, силы инерции и силу полезного сопротивления.

Силы тяжести прикладываем в центрах масс, а точки приложения сил инерции определяются по теореме подобия.

Силы реакции являются внутренними, они уравновешенны внутри механизма, поэтому не переносятся на «рычаг» Жуковского.

 

Составляем уравнение моментов относительно полюса р.

 

 

 

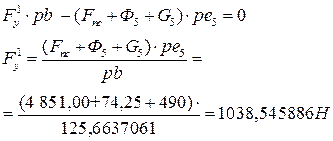
Находим уравновешивающий момент

 

 

Определяем относительную погрешность расчета

 

 

Относительная погрешность не должна превышать 5%. При выполнении этого условия силовой расчет рычажного механизма заканчивается.

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Курсовое проектирование по теории машин и механизмов: Учеб. Пособие для машиностр. Спец. Вузов / под ред. С.А. Попов, Г.А. Тимофеев. М.: Высш. Школа, 1988. 350 с.

 

2. Теория механизмов и машин: Учебник для втузов / И.И. Артоболевский. М.: Наука, 1988. 640 с.

 

3. Синтез и исследование рычажных механизмов: Методические указания к курсовой работе по теории механизмов и машин для студентов механических и машиностроительных специальностей / Сост. Б.Т. Фурсов, В. В. Носов. Липецк: ЛГТУ, 2003, 21 с.