 , (26)
, (26)
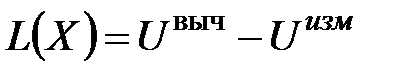 , (27)
, (27)
 . (28)
. (28)
Дополнительные критериальные функции
 , (29)
, (29)
 , (30)
, (30)
М – ошибка положения:
В одномерном случае 
В двухмерном случае 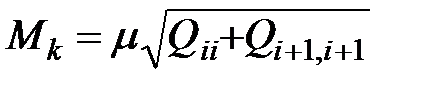 и т.д.
и т.д.
 , (31)
, (31)
 , (32)
, (32)
где N – количество уравнений; T – число параметров;
 , (33)
, (33)
 . (34)
. (34)
Исследования показали, что программы МК-метода дают решения близкие к «истине» и лучшие, чем метод наименьших квадратов, показатели оценки точности результатов уравнивания в 94,6% случаев [1-5].
Таблица 1. Результаты вычислений по программе GAUSS
| №№ п/п | Метод построения | S м | σ"β | σS мм | N | T | M1 м | M2 м | ΣδХ м | M3 м | [pvv] | характеристика укл. от истины |
| триангуляция | 1,0 | - | 0,025 | 0,065 | 1,1-05 | 2,3-02 | 40,001 | 2,6118 | ||||
| трилатерация | - | 0,097 | 0,222 | 1,5-02 | 1,8-01 | 4,0103 | 0,8912 | |||||
| л – у сеть | 1,0 | 0,034 | 0,083 | 1,5-04 | 1,7-02 | 67,002 | 5,5658 | |||||
| полигонометрия | 1,0 | 0,006 | 0,098 | 2,2-04 | 6,5-02 | 6,003 | 0,5858 | |||||
| триангуляция | 10,0 | - | 0,006 | 0,062 | 1,1-05 | 2,2-02 | 40,001 | 2,4665 | ||||
| трилатерация | - | 0,084 | 0,111 | 1,9-03 | 8,9-02 | 4,0026 | 0,4436 | |||||
| л – у сеть | 10,0 | 0,007 | 0,065 | 1,5-04 | 1,5-02 | 67,001 | 4,3383 | |||||
| полигонометрия | 10,0 | 0,001 | 0,077 | 2,3-04 | 4,8-02 | 6,0016 | 0,4623 | |||||
| простр. сеть | 2,0 | 0,013 | 0,012 | 2,5-07 | 2,6-03 | 113,00 | 1,4117 | |||||
| простр. сеть | 30,0 | 0,103 | 0,097 | 4,7-04 | 1,8-02 | 113,00 | 11,0016 | |||||
| равноточ. нив. | - | - | - | 2,5мм | 1,9-15 | 1,3мм | 4,6917 | 11,800 | ||||
| неравнот. нив. | - | - | - | 2,6мм | 1,6-15 | 1,8мм | 4,7347 | 12,522 | ||||
| равноточ. нив. | - | - | - | 2,5мм | 6,7-16 | 6,3-01 | 4,6917 | 11,915 | ||||
| неравнот. нив. | - | - | - | 3,0мм | 3,3-16 | 6,5-01 | 4,7107 | 14,3089 | ||||
| равноточ. нив. | - | - | - | 2,6мм | 2,2-16 | 1,4мм | 6.0505 | 15,9378 | ||||
| неравнот. нив. | - | - | - | 3,2мм | 8,9-16 | 1,5мм | 6,0873 | 19,5503 |
Таблица 2. Результаты вычислений по программе Mizkevich
| №№ п/п | Метод построения | S м | σ"β | σS мм | N | T | M1 м | M2 м | ΣδХ м | M3 м | [pvv] | характеристика укл. от истины |
| триангуляция | 1,0 | - | 0,025 | 0,040 | 9,4-03 | 2,2-02 | 40,3085 | 1,5960 | ||||
| трилатерация | - | 0,097 | 0,168 | 1,1-02 | 1,6-01 | 4,0067 | 0,6733 | |||||
| л – у сеть | 1,0 | 0,034 | 0,050 | 4,0-01 | 1,6-02 | 67,4744 | 3,3561 | |||||
| полигонометрия | 1,0 | 0,006 | 0,058 | 1,2-02 | 8,6-02 | 6,2486 | 0,3638 | |||||
| триангуляция | 10,0 | - | 0,006 | 0,001 | 3,6-06 | 3,4-05 | 63,9414 | 0,0066 | ||||
| трилатерация | - | 0,084 | 0,087 | 1,9-02 | 8,3-02 | 4,0015 | 0,3480 | |||||
| л – у сеть | 10,0 | 0,007 | 0,002 | 2,7-04 | 6,4-05 | 94,8417 | 0,0160 | |||||
| полигонометрия | 10,0 | 0,001 | 0,001 | 1,3-04 | 3,6-04 | 25,7423 | 0,0193 | |||||
| простр. сеть | 2,0 | 0,013 | 0,007 | 1,2-02 | 2,7-03 | 114,242 | 0,8357 | |||||
| простр. сеть | 30,0 | 0,103 | 0,013 | 5,6-02 | 5,5-03 | 135,121 | 1,7857 | |||||
| равноточ. нив. | - | - | - | 2,7мм | 4,2-15 | 1,1мм | 4,5366 | 12,251 | ||||
| неравнот. нив. | - | - | - | 2,2мм | 3,0-15 | 1,9мм | 4,5370 | 10,016 | ||||
| равноточ. нив. | - | - | - | 2,5мм | 2,7-15 | 6,4-01 | 4,4710 | 11,227 | ||||
| неравнот. нив. | - | - | - | 3,0мм | 2,4-15 | 5,5-01 | 4,3580 | 13,004 | ||||
| равноточ. нив. | - | - | - | 2,8мм | 6,7-16 | 1,4мм | 5,0725 | 16,0896 | ||||
| неравнот. нив. | - | - | - | 2,8мм | 3,8-15 | 1,7мм | 5,6800 | 16,0631 |
Таблица 3. Результаты вычислений по программе TIXONOV
| №№ п/п | Метод построения | S м | σ"β | σS мм | N | T | M1 м | M2 м | ΣδХ м | M3 м | [pvv] | характеристика укл. от истины |
| триангуляция | 1,0 | - | 0,025 | 0,030 | 6,0-03 | 4,0-03 | 51,0236 | 1,5642 | ||||
| трилатерация | - | 0,097 | 0,118 | 4,5-02 | 2,3-02 | 15,1209 | 1,7841 | |||||
| л – у сеть | 1,0 | 0,034 | 0,028 | 2,1-02 | 1,3-03 | 74,6442 | 2,2054 | |||||
| полигонометрия | 1,0 | 0,006 | 0,044 | 9,4-03 | 1,0-02 | 17,1904 | 0,7538 | |||||
| триангуляция | 10,0 | - | 0,006 | 0,029 | 5,9-03 | 4,0-03 | 51,6234 | 1,4768 | ||||
| трилатерация | - | 0,084 | 0,059 | 2,2-02 | 1,1-02 | 15,1209 | 0,8946 | |||||
| л – у сеть | 10,0 | 0,007 | 0,023 | 1,4-02 | 1,1-03 | 70,0660 | 1,8134 | |||||
| полигонометрия | 10,0 | 0,001 | 0,032 | 1,1-03 | 1,4-02 | 14,5376 | 0,4675 | |||||
| простр. сеть | 2,0 | 0,013 | 0,005 | 1,5-03 | 6,7-06 | 139,970 | 0,6473 | |||||
| простр. сеть | 30,0 | 0,103 | 0,026 | 8,3-03 | 6,5-04 | 139,782 | 3,7109 | |||||
| равноточ. нив. | - | - | - | 2,5мм | 3,0-15 | 1,2мм | 4,3567 | 11,017 | ||||
| неравнот. нив. | - | - | - | 2,6мм | 3,9-16 | 5,6-01 | 4,4512 | 11,802 | ||||
| равноточ. нив. | - | - | - | 2,6мм | 0,0-00 | 3,2-01 | 4,3566 | 11,321 | ||||
| неравнот. нив. | - | - | - | 3,1мм | 7,2-16 | 1,4мм | 4,3974 | 13,547 | ||||
| равноточ. нив. | - | - | - | 2,7мм | 1,9-15 | 6,5-01 | 5,7764 | 15,418 | ||||
| неравнот. нив. | - | - | - | 3,2мм | 1,3-15 | 8,2-01 | 5,8703 | 18,501 |
Таблица 4. Результаты вычислений по программе Budo
| №№ п/п | Метод построения | S м | σ"β | σS мм | N | T | M1 м | M2 м | ΣδХ м | M3 м | [pvv] | характеристика укл. от истины |
| триангуляция | 1,0 | - | 0,025 | 0,020 | 6,4-04 | 2,5-04 | 63,8906 | 1,2615 | ||||
| трилатерация | - | 0,097 | 0,048 | 1,0-00 | 3,0-01 | 77,6324 | 3,7474 | |||||
| л – у сеть | 1,0 | 0,034 | 0,018 | 2,0-02 | 9,6-03 | 73.6821 | 1,3154 | |||||
| полигонометрия | 1,0 | 0,006 | 0,032 | 4,2-01 | 2,4-02 | 5,8476 | 0,1847 | |||||
| триангуляция | 10,0 | - | 0,006 | 0,026 | 3,6-07 | 2,9-07 | 63,9998 | 1,6439 | ||||
| трилатерация | - | 0,084 | 0,037 | 5,3-01 | 2,6-01 | 948,123 | 37,318 | |||||
| л – у сеть | 10,0 | 0,007 | 0,017 | 6,9-02 | 1,1-02 | 47,5172 | 0,7964 | |||||
| полигонометрия | 10,0 | 0,001 | 0,050 | 4,9-01 | 8,7-03 | 289,01 | 14,476 | |||||
| простр. сеть | 2,0 | 0,013 | 0,005 | 7,2-03 | 6,5-03 | 97,3570 | 0,4714 | |||||
| простр. сеть | 30,0 | 0,103 | 0,018 | 1,3-00 | 3,1-02 | 110,557 | 1,9474 | |||||
| равноточ. нив. | - | - | - | 1,7мм | 1,0-13 | 5,6-03 | 8,9891 | 15,401 | ||||
| неравнот. нив. | - | - | - | 1,9мм | 6,8-14 | 1,2-02 | 8,9901 | 17,499 | ||||
| равноточ. нив. | - | - | - | 1,4мм | 2,1-13 | 3,6-03 | 8,9891 | 13,115 | ||||
| неравнот. нив. | - | - | - | 2,0мм | 8,3-15 | 7,8-03 | 8,9860 | 18,058 | ||||
| равноточ. нив. | - | - | - | 1,7мм | 4,0-13 | 8,8-03 | 11,986 | 20,027 | ||||
| неравнот. нив. | - | - | - | 2,2мм | 4,0-13 | 1,0-02 | 11,984 | 26,881 |
ЛИТЕРАТУРА
1. Мицкевич, В.И. Решение примера академика А.Н. Тихонова по обработке нивелирных сетей по программному комплексу «Россия-Беларусь» методом исключения строк из матрицы коэффициентов параметрических уравнений поправок / В.И. Мицкевич, [и др.] // Вестн. Полоц. гос. ун-та. Серия F. Строительство. Прикладные науки. – 2012. - №16. - С. 126 - 131.
2. Мицкевич, В.И. Обработка антирядов измерений одной величины при разных значениях количества неизвестных и разных характеристиках точности измерений с помощью программного комплекса «Россия-Беларусь» / В.И. Мицкевич, [и др.] // Вестн. Полоц. гос. ун-та. Серия F. Строительство. Прикладные науки. – 2012. - №16. - С. 109 - 113.
3. Субботенко, П.В. Развитие многокритериального способа уравнивания /П.В. Субботенко // Вестн. Полоц. гос. ун-та. Серия F. Строительство. Прикладные науки. – 2009. - №12. - С. 90 - 94.
4. Будо, А.Ю. О применении обобщенных нетрадиционных методов уравнивания /А.Ю. Будо // Вестн. Полоц. гос. ун-та. Серия F. Строительство. Прикладные науки. – 2009. - №12. - С. 136 - 141.
5. Мицкевич, В.И. Альтернативные методы проектирования и уравнивания геодезических сетей/В.И. Мицкевич, А.Ю. Будо, Е.В. Грищенков.- Новополоцк: ПГУ, 2008.- 280с.






