Математична лінійна регресійна модель y(x) має вигляд: y(x) = bo + b1·x,
де bo - вільний член, b1 - коефіцієнт впливу x на y. В завданні, що пропонується студенту, необхідно чисельно визначити значення bo та b1 за формулами:
Після закінчення розрахунків bо та b1 проводиться перевірка гіпотези про лінійність зв'язку між y та x за допомогою коефіцієнта лінійної кореляції R (як оцінити отриману модель на адекватність статистичним даним покажемо на прикладі двофакторної лінійної регресії):
Чим ближче значення /R/ до одиниці, тим вірогідніша лінійність y(x). При цьому знак R визначається знаком коефіцієнта b1 (якщо b1>0, то і R > 0 і навпаки). Вважається, що лінійна модель якнайкраще описує досліджуваний процес, якщо /R/≥ 0,7.
2. Математична модель, що є лінійною моделлю з двома змінними (факторами) y(x1;x2), має вигляд: y = bo + b1·x1 + b2·x2. Зробивши висновки, аналогічні для моделі y(x), можна отримати систему рівнянь відносно невідомих коефіцієнтів bo, b1, b2 у вигляді:
(x'1i)2 b1 + (x'1ix'2i)b2 = (x'1iy'i)
(x'2ix'1i)b1 + (x'2i)2 b2 = (x'2iy'i)
де:
x'1iy'i = (x1iyi) – N 
(x'1i)2 = (x1i)2 – N(
)2
x'2iy'i = (x2iyi) – N 
x'1ix'2i = (x1ix2i) –N 
(x'2i)2 = (x2i)2 – N (
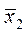)2
Після того, як величини, що входять в формули (10) - (14) розраховані, розв'язується система рівнянь (9) відносно bo, b1, b2 за допомогою правила Крамера.
Коефіцієнт b1 в моделі y = bo + b1x1 носить назву "повний коефіцієнт регресії", який відображає вплив x1 на y без урахування впливу x2 на y (цей вплив враховується певним чином в значенні b1).
Напроти, коефіцієнт b1 в моделі y = bo + b1·x1 + b2·x2 носить назву "частинний коефіцієнт регресії" (іноді - "чистий коефіцієнт регресії"), який відображає тільки вплив x1 на y, виключаючи повністю вплив x2 на y. Те ж саме стосується коефіцієнта b2. Тому потрібно пам'ятати, що врахування найбільшої (в розумних межах) кількості змінних поліпшує точність оцінки впливу кожної з розглянутих змінних.
2. Аналіз отриманих моделей.
Для оцінки моделей з багатьма змінними, а також з однією змінною, застосовуються наступні показники варіації:
1) Загальна дисперсія:
2) Факторна дисперсія, що відображує вплив тільки тих змінних, які розглядаються:
3) Залишкова дисперсія (дисперсія помилок моделі):
або в більш спрощеному вигляді
Відношення
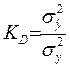
називається коефіцієнтом детермінації (у випадку лінійної множинної регресії) або індексом детермінації (у випадку нелінійної множинної регресії). Фізично він характеризує частку впливу вибраних змінних хj в загальній варіації у.
де R – коефіцієнт множинної кореляції (або індекс кореляції для нелінійної регресії). Значення цього коефіцієнта, розрахованого за даною формулою, співпадає зі значенням R, розрахованим за формулою для лінійної парної регресії. З урахуванням того, що 
, маємо ще одну розрахункову формулу:
тобто коефіцієнт кореляції розраховується по дисперсії помилок моделі 
і по загальній дисперсії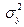 
.
Рекомендована література.
1. Корн Г., Корн Т. Справ очник по математике. М.,Наука, 1973, - 832с.
2.Кофман А., Анри-Лабердер А. Методы и модели исследования операций. – М., Мир, 1977, - 432с.
3. Четверухін Б.М. Методические разработки по курсу “Основы научных исследо-
ваний». Раздел «Дисперсионный анализ». – К.: КАДИ, 1977. – 31 с.
4. Четверухін Б.М. Методические разработки по курсу “Основы научных исследова-
ний». Раздел «Регрессионный анализ». – К.: КАДИ, 1977. – 29 с.
5. Робоча програма та методичні вказівки з дисципліни „Основи теорії систем і системного аналізу. Методичні вказівки та завдання для самостійних робіт для студентів спеціальностей 7.100.403 "Організація перевезень та управління на транспорті" денної та заочної форм навчання / Укл. С.Д.Радкевич, О.Д.Гульчак, Савченко Л.В. - К: НТУ, 2006. - 28 с.
