Вступ
Курсова робота з теорії автоматичного керування (ТАК) ставить за мету освоєння методів аналізу і синтезу цифрової системи автоматичного регулювання (САР) із зворотним зв’язком. Для реалізації цих задач в курсову роботу включені такі традиційні питання як визначення передатної функції системи за її структурною схемою, визначення стану стійкості системи, визначення показників якості перехідного процесу системи, розрахунок і побудова частотних характеристик системи, розрахунок точності керування, корекція системи і синтез схеми коректованого регулятора.
В завданні на курсову роботу задані допустимі значення показників якості регулювання, які задовольнять вимогам якості перехідного процесу, стійкості і точності регулювання. Цифрова система в курсовій роботі розглядається як цифрова модель неперервної системи, для якої в завданні на курсову роботу задані значення параметрів усіх її ланок.
В першій частині курсової роботи виконується аналіз процесу регулювання заданої некоректованої системи. Для неї розраховуються значення регламентованих показників якості керування, які порівнюються із заданими допустимими значеннями. Оскільки деякі з розрахованих параметрів не задовольняють поставленим вимогам, приймається рішення про необхідність корекції, яка реалізується в другій частині курсової роботи.
Для реалізації корекції визначається передатна функція коректованої системи. Корекція повинна поліпшити певні показники системи регулювання. Для того, щоб у цьому пересвідчитись і кількісно оцінити ефект корекції передбачається контрольний розрахунок параметрів коректованої системи. У випадку позитивного ефекту корекції виконується синтез коректованого цифрового регулятора у вигляді різницевого рівняння і відповідної схеми цифрового фільтру.
Ряд розрахунків і побудову їх графіків зручно виконувати на ПЕОМ за допомогою математичного пакету програм (наприклад, MathCad) а також за допомогою спеціалізованих учбових програм з курсу ТАК, розміщених на ПЕОМ у дисплейному класі кафедри.
Курсова робота повинна бути старанно оформленою. Таблиці і рисунки повинні бути перенумерованими і мати підписи. В тексті потрібно посилатись на таблиці і рисунки, а також на літературні і програмні джерела інформації. Текст повинен бути старанно написаним з дотриманням граматичних і синтактичних правил. Рисунки виконуються за допомогою креслярських інструментів або друкуються на принтері. Текстові пояснення до розрахунків і висновки пишуться від руки. Коментарі до машинних розрахунків і самі машинні розрахунки можуть бути надрукованими на принтері. Розрахунки без коротких текстових пояснень не допускаються. Текстові пояснення до розрахунків повинні бути стислими і конкретними, загальний обсяг КР, як правило, не повинен перевищувати 15-20 сторінок стандартного формату А4.
До оформленої за правилами стандартів курсової роботи додається демонстраційний плакат формату А1, який використовується для демонстрації основних результатів роботи під час її захисту. Студент самостійно вирішує, який матеріал винести на демонстраційний плакат для того, щоб його доповідь була впевненою і переконливою.
У вступі до курсової роботи потрібно привести структурно-функціональну електричну схему заданої системи. Якщо задана, наприклад, система фазового авторегулювання частоти, то на функціональній схемі потрібно показати усі функціонально необхідні пристрої системи, зокрема фазовий детектор, фільтр, підсилювач і керований генератор. В описі схеми потрібно пояснити принцип дії системи і призначення кожного її пристрою, скориставшись описом відповідних пристроїв системи в літературі [2, 6].
1. Структурна схема і передатні функції неперервної системи
Розглянемо структурну схему і ряд наступних питань на прикладі завдання на тему “Аналіз і синтез цифрової системи фазового авторегулювання частоти”. У розділі початкових даних і вимог до процесу керування цього завдання сказано, що аналоговий прототип цифрової системи фазового авторегулювання частоти (ЦФАРЧ) складається з таких функціонально необхідних елементів: фазовий детектор (ФД), інтегратор (І), підсилювач (П) і керований електронний генератор (КГ). Неперервними моделями ФД і КГ є інерційні ланки з параметрами відповідно k1, Т1 і k2, Т2. Коефіцієнт підсилення підсилювача дорівнює kо, а інтегратора – одиниця.
З приведеного опису заданої системи неважко установити, що фазовий детектор моделюється інерційною ланкою з передатною функцією (ПФ) 
, інтегруючий пристрій – ідеальною інтегруючою ланкою з ПФ W2(s) =1/s, підсилювач – пропорційною ланкою з ПФ W3 (s) = k0, керований електронний генератор – інерційною ланкою з ПФ 
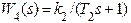. Тому структурна схема неперервної моделі заданої системи матиме такий вигляд як на рис.1.1.
 |
Рис.1.1. Структурна схема аналогового прототипу заданої системи
Передатна функція ланцюга ланок неперервної системи має такий вигляд:
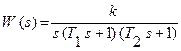, (1.1)
де 
–загальний коефіцієнт підсилення системи.
Передатна функція у вигляді (1.1) відображає структурну схему розімкненої частини заданої системи. Тому подібну форму ПФ будемо називати структурною. Вона зручна для розрахунку частотних характеристик системи. Передатну функцію, представлену у вигляді відношення двох многочленів, називають дробово-раціональною. Вона для заданої системи має такий вигляд:
, (1.2)
де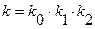 
- загальний коефіцієнт підсилення системи.
Передатна функція замкненої неперервної системи
. (1.3)
В цьому розділі курсової роботи представте структурну схему системі, визначте її передатні функції з розрахованими числовими значеннями коефіцієнтів b 0, a 0, a 1, a 2, a 3. Запишіть передатну функцію кожного виду як у символьній формі, так і у числовій формі.
2. Структурна схема і передатні функції цифрової системи
Схема цифрової системи з цифровим керуючим пристроєм і цифровим об’єктом керування приведена на рис.2.1. В заданій системі до складу моделі керуючого пристрою входять перша інерційна ланка, інтегратор і підсилювач, а об’єкт керування представлений другою інерційною ланкою. На вході цифрової системи передбачений аналого-цифровий перетворювач, оскільки припускається, що вхідний сигнал неперервний.
 |
Рис. 2.1. Схема цифрової САР
При великій розрядності АЦП (порядка 8-10), яка практично завжди має місце, цифровий сигнал на виході АЦП замінюють дискретним у часі. Це дає можливість одержати відносно просту модель цифрової системи, структурна схема якої представлена на рис. 2.2. В ній АЦП явно представлений тільки імпульсним елементом, який перетворює неперервний сигнал в дискретний.
За допомогою цифрової моделі спроектуємо цифрову систему з характеристиками, близькими до характеристик неперервної системи. Дискретну передатну функцію W(z) розімкненої частини цифрової системи знайдемо методом білінійного перетворення, яке реалізується підстановкою
, (2.1)
у відповідну неперервну ПФ W(s). Тут Т –інтервал дискретизації.
 |
Рис. 2.2. Структурна схема моделі цифрової системи
Результатом підстановки (2.1) в (1.2) буде дробово-раціональний вираз виду
, (2.2)
з коефіцієнтами
d 0=k, d 1=3k, d 2=3k, d 3=k,
c 0=T1p2+T2p2+T1T2p3+p, c 1= -T1p2-T2p2 -3T1T2p3+p,
c 2= -T1p2-T2p2 +3T1T2p3-p, c 3= T1p2+T2p2 -T1T2p3-p.
Для обчислення коефіцієнтів c i потрібно інтервалу дискретизації T надати числове значення, яке вибирають не більшим 1/100 від практичної тривалості q перехідного процесу в неперервній системі або визначають через частоту дискретизації wд як T=2p/wд. Частоту дискретизації вибирають в декілька (4-8) разів більшою від граничної частоти АЧХ замкненої неперервної системи. В даній курсовій роботі доцільно скористатись рекомендацією, яка не вимагає попереднього розрахунку неперервної системи і яка полягає в тому, що інтервал дискретизації Т вибирають рівним (Т1+Т2)/10.
Передатну функцію замкненої цифрової системи знайдемо по аналогії з передатною функцією неперервної системи з виразу
Ф(z) = W(z)/[1+W(z)]. (2.3)
Підставивши сюди вираз для W(z), одержимо Ф(z) у вигляді
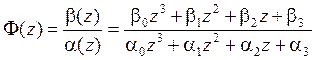, (7.5)
де bi= d i, αi=(c i+ d i), i =0,1,2,3.
Результатами цього розділу курсової роботи повинні бути структурна схема моделі цифрової системи і вирази для передатних функцій W(z) і Ф(z) у вигляді відношення многочленів від змінної z з і визначеними числовими значеннями коефіцієнтів цих многочленів.
3. Визначення стану стійкості цифрової системи
Цифрова система (ЦС) визначається своєю z-передатною функцією, яка у попередньому розділі КР одержана у такому загальному вигляді:
. (3.1)
Необхідна і достатня умова стійкості ЦС вимагає, щоб усі полюси передатної функції системи zi, i =1,2,… n, де n – порядок ЦС, знаходились в середині круга комплексної площини Z з радіусом круга R=1, тобто, щоб модулі усіх коренів знаменника передатної функції були меншими одиниці. Значення zi=1 відповідає границі стійкості системи. Полюси передатної функції ЦС – це корені її характеристичного рівняння α(z)= 0, де α(z) – знаменник ПФ Ф(z) замкненої системи.
У цьому розділі курсової роботи для визначення стану стійкості ЦС знайдіть корені її характеристичного рівняння
α(z)=0, (3.2)
визначте їх модулі і впевніться у тому, що вони менші одиниці. Це свідчитиме про стійкість цифрової системи. Якщо попередні перетворення виконані правильно і правильно розв’язане характеристичне рівняння, то умова стійкості цифрової системи як дискретного аналога стійкої неперервної системи буде виконана.
4. Дослідження перехідного процесу цифрової системи
Якщо вхідну дію цифрової системи позначити як x (nТ), а вихідну як y (nТ), то передатну функцію ЦС можна записати у такому загальному вигляді
Φ(z) =Y(z)/X(z)=B(z)/A(z), (4.1)
де B(z) і A(z) – многочлени відповідно чисельника і знаменника ПФ,
X(z) i Y(z) – z-зображення відповідно вхідної і вихідної дій.
З (4.1) одержуємо рівняння:
A(z)∙Y(z) = B(z)∙X(z). (4.2)
Раніше ПФ заданої системи одержана у такому загальному вигляді:
. (4.3)
Поділивши одержаний вираз на старший член знаменника (a0∙z3), представимо передатну функціюΦ(z) в такій формі
. (4.4)
Підставивши з (9.4) B(z) і A(z) в (9.2), одержимо
. (4.5)
Перейдемо тепер від зображень X(z) i Y(z) до оригіналів x (n T) i y (n T). При цьому зважимо на те, що множних z-k відповідає запізненню оригінала на k інтервалів дискретизації Т. В результаті одержимо різницеве рівняння системи у вигляді
. (4.6)
Рівняння (4.6) доповнюється нульовими початковими умовами:
y (-T)=0, y (-2T)=0, y (-3T)=0.
Дискретна вхідна дія
x (nT)=0 при n< 0.
Різницеве рівняння дає можливість розрахувати значення вихідного сигналу y (nТ) в дискретні моменти часу nТ при відомих значеннях вхідного сигналу x (nT) в дискретні моменти nТ. Оскільки при x (nT)=1(nT) вихідна дія y (nT)= h (nT), рівняння (4.6) можна переписати у пристосованому для розрахунку перехідної характеристики вигляді
. (4.7)
Різницеве рівняння як рекурентне відношення між попереднім і наступним значеннями вихідної величини є досить зручною математичною моделлю ЦС. Воно дозволяє розрахувати часові і частотні характеристики ЦС, подаючи потрібний для тієї чи іншої характеристики вхідний сигнал x (nТ) і послідовно обчислюючи значення y (nТ).
У даному розділі КР потрібно одержати різницеве рівняння заданої системи у вигляді (4.7) з розрахованими коефіцієнтами a i, b j (i=1,2,3; j=0,1,2,3), які визначаються через параметри системи k, T 1, T 2 та інтервал дискретизації T, рекомендації для вибору якого були дані раніше. Розв’яжіть одержане різницеве рівняння на ПЕОМ за допомогою будь-якого математичного пакету програм. Програмою MathCad розв'язок рівняння (4.7) виконується таким обчислювальним фрагментом:
З результатів розрахунку h (nT) визначте (з останнього входження процесу в 5-процентний коридор відносно усталеного значення) практичну тривалість перехідного процесу q, визначте також величину перерегулювання s% і порівняйте їх з заданими значеннями в завданні на курсову роботу.
Для перевірки правильності розрахунку перехідної характеристики скористайтесь кафедральною учбовою програмою PerHarCS.
5. Частотні характеристики цифрової системи
Відомо, що частотні характеристики цифрової і неперервної систем порівнювати можна тільки в діапазоні частот від 0 до половинної частоти дискретизації p/T, де вони можуть бути подібними але не можуть для реальних систем точно співпадати між собою. Частотну передатну функцію W(w) цифрової системи одержують заміною в дискретній ПФ змінної z на wТ за допомогою виразу:
z = exp(jwT) = cos(ω∙T) + j∙sin(ω∙T). (5.1)
Тут враховано, що z=exp(sT) і що для переходу до частотної ПФ потрібна заміна змінної s на jw. Для розрахунку частотних характеристик розімкненої частини заданої ЦС скористаємось знайденою раніше її дискретною передатною функцією
,
у якій замінимо змінну z на cos(ω∙T) + j∙sin(ω∙T). Результатом заміни буде комплексна частотна передатна функція W(w). Комплексні вирази у чисельнику і знаменнику цієї функції представимо спочатку у комплексно-алгебраїчній формі
, (5.2)
де
Для подальших розрахунків представимо комплексні вирази чисельника і знаменника частотної ПФ в експоненціальній формі
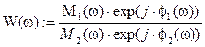(5.3)
де
,
,
При обчисленні величин f1(w) і f2(w) програмою MathCad можна скористатись функцією atan2(x,y) або angle(x,y) дійсних аргументів x і y, яка повертає повний кут в радіанах між х- віссю і лінією, що сполучає початок координат з точкою (x,jy) на площині комплексних чисел або з точкою (x, y) на площині дійсних чисел.
Амплітудно-частотну характеристику розімкненої ЦС визначимо з (5.3) як
A(w)=|W(w)|=M1(w) / M2(w), (5.4)
а фазово-частотну характеристику як
j(w)=arg W(jw)=f1(w) - f2(w). (5.5)
Подібним до описаного способом, виходячи з ПФ Φ(z), можна розрахувати частотні характеристики замкненої цифрової системи, але простіше це зробити за допомогою формул
, (5.6)
, (5.7)
для розрахунку частотних характеристик замкненої системи через частотні характеристики розімкненої системи, оскільки ці формули, справедливі для неперервних систем, залишаються справедливими і для цифрових систем.
У курсовій роботі розрахуйте і побудуйте графіки АЧХ і ФЧХ розімкненої і замкненої ЦС в діапазоні частот від 0 до wд/2=p/T, де wд=2p/T – частота дискретизації. При виборі розрахункових частот w можна орієнтуватись на значення w=[0, 1, 5, 10, (1/T1), (1/T2), wд/2, ¥] та інші. Звичайно не всі зазначені та інші частоти можуть бути використані для побудови кожного графіка, оскільки потрібно зобразити ту частину характеристики, з якої зручно і наглядно визначаються необхідні параметри системи. Наприклад, графік АЧХ повинен бути зручним для визначення параметрів wз і DА, а графік ФЧХ – для визначення ∆j і wp.З графіків АЧХ і ФЧХ розімкненої системи визначте частоту зрізу wз, частоту wp і відповідно запас стійкості з фази Dj і запас стійкості з амплітуди DA. Порівняйте одержані запаси стійкості з відповідними параметрами в завданні на курсову роботу. З графіка АЧХ замкненої системи визначте ширину ефективного діапазону частот з рівнем значимості 0,707.
Перевірте правильність виконаних розрахунків частотних характеристик цифрової системи за допомогою кафедральної учбової програми ChastHarCF.
6. Розрахунок точності роботи цифрової системи
Точність цифрової системи оцінюють помилкою керування в усталеному режимі роботи системи. Помилка системи може бути знайдена з її z-зображення за допомогою теореми про кінцеве значення. Більш загальний підхід до визначення помилки пов’язаний з формулою розкладання її в ряд Тейлора
e(n T) = С 0 u (n T) + С 1 u ¢(n T) + ½ С 2 u ² (n T) + … + (1/k!) С k u (k) (n T), (6. 1 )
де С 0, С 1, С 2, … – коефіцієнти помилок стану, швидкості, прискорення і так далі, u (n T) – вхідна дія.
Коефіцієнт помилки Сk цифрової системи можна знайти з формули
, (6.2)
яка аналогічна формулі для помилки неперервної системи, але зручніше користуватись такими еквівалентними відносно (11.2) формулами, в яких виконана заміна еst= z:
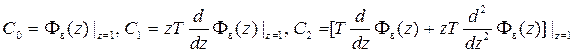. (6.3)
Для визначення коефіцієнтів помилок С 0, С 1, С 2 цифрової системи знайдемо передатну функцію для помилки з формули
Фe(z)=1/[1+W(z)]. (6.5)
Підставивши в (11.5)
,
знайдемо ПФ замкненої ЦС у такому вигляді:
, (6.6)
де ei = ci + di, i =0,1,2,3.
Фрагмент обчислення коефіцієнтів програмою MathCad для одного з варіантів подібної задачі має такий вигляд:
.
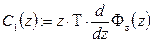
Одержані значення коефіцієнтів помилок для цифрової системи порівняйте з коефіцієнтами в завданні на курсову роботу.
Правильність виконаних розрахунків перевірте за допомогою кафедральної учбової програми TochnistCS.
7. Корекція цифрової системи
7.1. Передатні функції коректованої цифрової системи
Порівнюючи розраховані вище показники якості перехідного процесу q і s для цифрової системи з відповідними заданими значеннями цих показників, помічаємо, що розрахована цифрова система не задовольняє заданим вимогам. Тому за допомогою цифрової корекції системи спробуємо поліпшити згадані показники, не погіршуючи при цьому інших показників (∆А, ∆φ, С0, С1 і С2).
Розглядатимемо коректовану цифрову систему як дискретний аналог неперервної коректованої системи. В курсовій роботі пропонується застосувати часовий метод послідовної корекції типовими ланками корекції.
Методика часової послідовної корекції полягає в тому, що на основі аналізу впливу типових ланок корекції на динаміку системи [1-3] вибирають таку ланку, яка у заданій системі може дати позитивний ефект. Для заданої системи з метою зменшення тривалості перехідного процесу і величини перерегулювання застосовують форсуючу ланку з передатною функцією WК(s) = t s +1. Значення параметра t підбирають так, щоб досягти максимального ефекту корекції. Подібну задачу параметричної оптимізації можна розв’язати за допомогою спеціалізованих програм, призначених для автоматизованого проектування автоматичних систем, але в курсовій роботі обмежимось одним значенням параметра t. Візьмемо t=T1+T2, яке близьке до оптимального для систем заданої структури.
Після включення ланки корекції в ланцюг ланок неперервної системи передатна функція W(s) її розімкненої частини системи матиме вид
, (7.1)
а ПФ замкненої коректованої системи матиме вид
, (7.2)
для якої коефіцієнти b 0 = k t, b 1 = k, a 0 = Т1×Т2, a 1 =(Т1 + Т2), a 2 = (1 + k t), a 3 = k потрібно розрахувати при t=T1+T2.
Заміною z на (pz-p)/(z+1) в ПФ W(s) розімкненої неперервної коректованої системи одержимо ПФ W(z) розімкненої цифрової коректованої системи у такому вигляді:
. (7.3)
Коефіцієнти ei, ci в (13.1) обчислюють з формул
d 0=k×(τ×p+1), d 1=2×k×(τ×p+1)+ k×(-τ×p+1),
d 2=2×k×(-τ×p+1)+ k×(τ×p+1), d 3= k×(-τ×p+1),
c 0=T1p2+T2p2+T1T2p3+p, c 1= -T1p2-T2p2 -3T1T2p3+p,
c 2= -T1p2-T2p2 +3T1T2p3-p, c 3= T1p2+T2p2 -T1T2p3-p.
Помітимо, що коефіцієнти знаменника ci коректованої системи співпадають з раніше обчисленими коефіцієнтами ci у виразі (2.2) для ПФ некоректованої ЦС, чого не можна сказати про коефіцієнти чисельника di.
ПФ замкненої коректованої ЦС згідно з формулою Ф(z)=W(z)/[1+W(z)] матиме вид
. (7.4)
де a(z)=C(z)+D(z) і відповідно ai = ci + di, i =0,1,2,3,
b(z)=D(z) і відповідно bi = di.
В даному розділі курсової роботи потрібно розрахувати коефіцієнти многочленів передатних функцій W(z) і F(z).
7.2. Розрахунок показників якості керування коректованої системи
Знання передатних функцій цифрової коректованої системи дає можливість розрахувати основні показники якості q, s, ∆A, ∆φ, С1, С2 і С3 цієї системи по аналогії з раніше виконаними розрахунками для некоректованої цифрової системи. Розраховані показники якості регулювання для некоректованої і коректованої цифрових систем, а також задані значення показників якості, зведіть в порівняльну таблицю і зробіть висновки відносно ефективності корекції.
Синтез схеми цифрового регулятора з коректором
Оскільки ефект корекції позитивний, знайдемо передатну функцію Wr(z) цифрового керуючого пристрою (регулятора) з коректором і побудуємо структурну схему відповідного цифрового фільтра.
Для визначення різницевого рівняння цифрового регулятора і структурної схему відповідного цифрового фільтра (ЦФ) потрібно знайти передатну функцію регулятора. Передатна функція неперервного регулятора з ланкою корекції має вид
, (7.1)
де kr=k0×k1 – коефіцієнт підсилення регулятора.
Передатну функцію цифрового коректованого регулятора знайдемо заміною в передатній функції Wr(s) змінної s на (p×z-p)/(z+1). В результаті заміни одержимо передатну функцію цифрового регулятора у вигляді:
, (7.2)
де
b 0= krt p + kr, b 1= 2kr, b 2= - krt p + kr, a0= T 1 p 2+ p, a1= -2 T 1 p 2, a2= T 1 p 2- p.
Поділивши в (7.2) чисельник і знаменник на старший член знаменника, одержимо
, (7.3)
де
b 0=b 0/a0, b 1=b 1/a0, b 2=b 2/a0, a 1=a1/a0, a 2=a2/a0.
З (7.3) одержуємо таке диференціальне рівняння
, (2.4)
 |
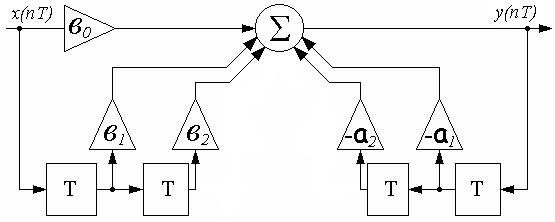якому відповідає реалізація цифрового регулятора коректованої системи, показана у вигляді структурної схеми цифрового фільтру на рис. 7.1.
Рис.7.1. Цифровий регулятор коректованої системи у вигляді структурної схеми цифрового фільтру
Структурна схема цифрового фільтра складається з елементів затримки на тактовий інтервал T, які відображають відповідні затримки в різницевому рівнянні, масштабних підсилювачів, які відображають коефіцієнти різницевого рівняння і суматора, який відображає алгебраїчну суму компонентів правої частини рівняння.
В даному розділі курсової роботи покажіть передатну функцію та різницеве рівняння і схему цифрового регулятора з обчисленими значеннями масштабних коефіцієнтів.
Додаток 2. Зміст титульної сторінки курсової роботи
Міністерство транспорту України
Дніпропетровський національний університет залізничного транспорту
Кафедра АТЗ
Дослідження цифрової системи автоматичного регулювання
Курсова робота з дисципліни “Теорія автоматичного керування”
Виконав студент гр. ___________
_____________________________
Перевірив ____________________
___ ____________ 200_ р.
Дніпропетровськ, Д І І Т, 2004 р.
Список літератури
1. Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989. – 256 с.
2. Солодовников В.В. и др. Основы теории и элементы систем автоматического регулирования. М.: Машиностроение, 1985. – 536 с.
3. Теория автоматического управления. В 2-х частях. Под ред.А.А.Воронова. М.: Высшая школа, 1986.
4. Руководство по проектированию систем автоматического управления. Под. ред. Бесекерского. М.: Высшая школа, 1983. – 296 с.
5. Безруков В. В., Гаврилюк В. І. Теорія автоматичного керування: Методичні вказівки до курсової роботи /Дніпропетр. нац. ун-т залізнич. трансп.; 2003. – 25с.
6. Абрамов В.М. Электронные устройства железнодорожной автоматики. М.: Транспорт, 1986. – 264 с.
7. Бронштейн И. Н. и Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1995.
