Тензор (2-го ранґу) – це змінна величина, яка визначається в будь-якій декартовій системі координат тривимірного простору 32=9 числами (компонентами)
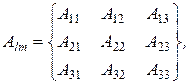
які під час повороту систем координат перетворяться в Ai’k’ згідно із законом
Аi′k′ = аi′l · аk′m · Аlm, (3.1.1)
де аi’l, аk’m – направляючі косинус переходу від старої до нової системи координат [1].
| Наприклад: а23 – косинус кута a між 2-ою віссю і 3-ою віссю старої системи координат. Оскільки індекси косинусів аi’l (та аk’m) набувають по три значення, існують дев'ять різних комбінацій індексів. Отже, орієнтація нової системи координат відносно |
старої задають дев'ятьма направляючими косинусами. Їх зручно зобразити у вигляді таблиці (табл. 3.1), в якій 1-й індекс косинуса належать до старої, а 2-й – до нової системи координат.
Таблиця 3.1 - Направляючі косинуси
| X′ | Y′ | Z′ | |
| Х | аxx′ | аxy′ | аxz′ |
| Y | аyx′ | аyy′ | аyz′ |
| Z | аzx′ | аzy′ | аzz′ |
Якщо всі дев'ять направляючих косинусів відомо, то за формулою (3.1.1) можна знайти компоненти тензора в новій системі координат. Звичайно відомо тільки три направляючі косинуси, оскільки орієнтація нової системи координат відносно старої однозначно визначається трьома кутами. Тому виникає необхідність у визначенні інших шести направляючих косинусів.
3.1.1 Записуємо відомі (задані) направляючих косинусів у табл. 3.2
Таблиця 3.2 - Відомі (задані) направляючих косинусів
| X′ | Y′ | Z′ | |
| Х | 0,623 | 0,74 | 0,254 |
| Y | 0,38 | -0,57 | 0,728 |
| Z | -0,683 | 0,357 | 0,636 |
У міру визначення інших направляючих косинусів їх значення потрібно занести до відповідних місць табл. 3.2
3.1.2 Знаходимо 
за рівнянням Ейлера для осі 
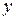
Знак визначає квадрант простору, в якому розглядають систему координат. Оскільки умовами задачі квадрант не обумовлений, вибираємо знак довільно. Хай 
.
3.1.3 Знаходимо косинуси для осі 
, використовуючи рівняння Ейлера та умову ортогональності вісей і 
:
.
Підставляючи відомі косинуси, маємо
(3.1.2)
Розв’язуючи отриману систему рівнянь, знаходимо два варіанти наборів направляючих косинусів для осі :
| 1-й варіант | 2-й варіант |
| 
|
| 
|
| 
|
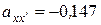
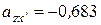
Проводимо перевірку, підставляючи отримані значення косинусів до формул (3.1.2)
1-й варіант
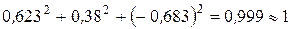
2-й варіант
З результатів перевірки випливає, що обидва варіанти направляючих косинусів, отже, обидва варіанти орієнтації нової системи координат у просторі, можливі. Відповідно до п. 1.2 вибираємо варіант довільно. Хай це буде 1-й варіант.
3.1.4 Знаходимо косинуси вісі 
, використовуючи рівняння Ейлера для цієї осі та умову ортогональності осей 
і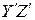 
:
Після підставлення відомих косинусів одержуємо:
. (3.1.3)
Розв’язучи систему (3.1.3), знаходимо два варіанти наборів направляючих косинусів:
| 1-й варіант | 2-й варіант |
| 
|
| 
|
| 
|
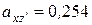
Проводимо перевірку, підставляючи значення косинусів обох варіантів до системи (3.1.3). Якщо обидва варіанти задовольняють системі (3.1.3), то вибираємо один з них довільно. Отримані значення косинусів заносимо до табл. 3.2.
Остаточну перевірку правильності визначення бракуючих направляючих косинусів проводимо, обчислюючи суми квадратів косинусів за рядками табл. 3.2. Вони мають дорівнювати 1 з точністю до 4-го знака після коми (щоб надалі компоненти тензора напруг у новій системі координат можна було знайти з похибкою 10%).
