3.4.1. Для визначення класу точності будь-якого засобу вимірювань (ЗВ) в
першу чергу знімають його статичну характеристику перетворення.
Статична характеристика перетворення ЗВ - відноситься до однієї із
основних метрологічних характеристик ЗВ і являє собою функціональну
залежність між вхідною вимірюваною величиною та вихідним сигналом ЗВ.
Для знімання статичної характеристики ЗВ, як правило, приводять до
взаємодії з мірами або еталонами. Статична характеристика знімається при
повільних змінах вхідного інформативного параметру (значення міри) і вихідного сигналу ЗВ в координатах: по осі абсцис – значення міри на вході ЗВ (Х0і), а по осі ординат – покази ЗВ (Хі), які відповідають значенням цієї міри в
усьому діапазоні вимірювання.
При цьому по діапазону вимірювання вибирають декілька точок, починаючи з мінімального значення міри (нульове значення міри) на початку, та закінчуючи максимальним значенням міри в кінці діапазону. Кожній точці діапазону вимірювання повинно відповідати певне значення міри (як правило
розподіл точок діапазону задають рівномірним).
3.4.2. В загальному випадку, для визначення наявності чи ні у ЗВ варіації,
знімають як пряму гілку перетворення в напрямку від нижньої межі діапазону до верхньої, збільшуючи міру від мінімального значення до максимального і фіксуючи покази ЗВ із сторони менших значень до більших Ximin, так і зворотну, зменшуючи міру на вході ЗВ від максимального її значення до мінімального і фіксуючи покази ЗВ із сторони більших значень до менших Ximax. Кількість циклів n ц (один цикл вміщує в собі збільшення та зменшення міри по діапазону вимірювань)вибирається як правило не менше 10 - 15, а загальна кількість n вимірювань, проведених в кожній точці, дорівнює в цьому
випадку: n = 2* n ц = 20 – 30.
3.4.3. Розраховують систематичну складову похибки (ССП) Δс ЗВ для
кожної точки характеристики перетворення. Для цього спочатку із отриманих
n результатів вимірювання Х1, Х2, Х3,...Xn, необхідно вирахувати середнє
арифметичне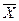 
цього ряду (математичне сподівання M[X]):
M[X]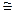 
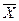= (1/n) ּ (X1+X2+X3+...+Xn) = (
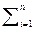Х 
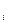)/n,
де Х і – це результати одиночних вимірювань (із загальної кількості n), що
проведені в даній точці, як прямої гілки перетворення (X imin), так і для зворотної
(Ximax).
Далі вираховується, з урахуванням знаку, ССП Δс, яка притаманна ЗВ в даній точці характеристики перетворення:
Δс = 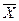– Х оі,
де Х оі -значення міри на вході ЗВ в даній точці.
3.4.4. 
Розраховують точкову оцінку середнього квадратичного відхилення Sx для кожної точки, якщо кількість проведених вимірювань n<2 0 за формулою:
Sx =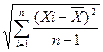 
,
де (Х і - 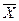) - це випадкова Δв складова похибки (ВСП) кожного одиночного
вимірювання (спостереження) в даній точці, яка визначається як рiзниця мiж результатом одиночного спостереження Х і та математичним сподіванням
результатiв вимірювання або середнім арифметичним в даній точці:
Δв = Х і - M[X] 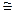Х і - .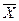
При кількості вимірювань n ≥ 20 середнє квадратичне відхилення
зображується як σ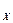 
і обчислюється за формулою:
σ =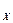 
.
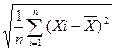3.4.5. Використовуючи розподіл Стьюдента для малої кількості вимірювань (n<20), визначають довірче значення Δ0,95 випадкової складової похибки, яке показує довірчу межу відхилення отриманих результатів вимірювання від їхнього середнього арифметичного (математичного сподівання mx). Іншими словами Δ0,95 - це складова похибки, яка оцінює інтервал невизначеності результатів вимірювання для кожної точки з довірчою ймовірністю Р д = 0,95. Вона дорівнює:
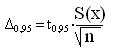, де t0,95 -коефіцієнтСтьюдента для Р д = 0,95 і n = 10 (t0,95 = 2,26).
