ћ»Ќ»—“≈–—“¬ќ ќЅ–ј«ќ¬јЌ»я » Ќј” » ” –ј»Ќџ
—≈¬ј—“ќѕќЋ№— »… Ќј÷»ќЌјЋ№Ќџ… ”Ќ»¬≈–—»“≈“ яƒ≈–Ќќ… ЁЌ≈–√»» » ѕ–ќћџЎЋ≈ЌЌќ—“»
Ћабораторное зан€тие є
по дисциплине "ѕ“÷ј"
на тему: "ћинимизаци€ логических функций методом вайна и реализаци€ их в различных базисах"
«адание выполнил:
—тудент 62? класса
____________
ѕоверил:
____________
—евастополь Ц 20 г.
“еоретические основы минимизации булевых функций методом вайна
ѕри проектировании цифровых автоматов широко используютс€ методы минимизации булевых функций, позвол€ющие получать рекомендации дл€ построени€ экономичных схем цифровых автоматов. ќбща€ задача минимизации булевых функций может быть сформулирована следующим образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимально возможное число букв. —ледует отметить, что в общей постановке данна€ задача пока не решена, однако достаточно хорошо исследована в классе дизьюнктивно-конъюнктивных нормальных форм.
ќпределение. Ёлементарной конъюнкцией называетс€ конъюнкци€ конечного числа различных между собой булевых переменных, кажда€ из которых может иметь или не иметь отрицани€.
ќпределение. ƒизъюнктивной нормальной формой (ƒЌ‘) называетс€ дизъюнкци€ элементарных конъюнкций.
ќпределение. ћинимальной дизъюнктивной нормальной формой булевой функции называетс€ ƒЌ‘, содержаща€ наименьшее число букв (по отношению ко всем другим ƒЌ‘, представл€ющим заданную булеву функцию).
ќпределение. Ѕулева функци€ 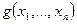 называетс€ импликантой булевой функции
называетс€ импликантой булевой функции 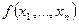 , если дл€ любого набора переменных, на котором g = 1, справедливо f =1.
, если дл€ любого набора переменных, на котором g = 1, справедливо f =1.
ѕример. Ѕулева функци€ f задана табл. 1. “ам же приведены все ее импликанты. ѕри записи функции f и ее импликант в —ƒЌ‘ имеем:
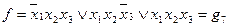

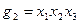
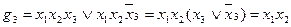
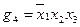

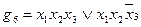
| “аблица 1 | ||||||||||
| x1 | x2 | x3 | f | g1 | g2 | g3 | g4 | g5 | g6 | g7 |
ќпределение. »мпликанта g булевой функции f, €вл€юща€с€ элементарной конъюнкцией, называетс€ простой, если никака€ часть импликанты g не €вл€етс€ импликантой функции f.
»з примера видно, что импликанты 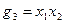 и
и 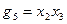 , €вл€ютс€ простыми импликантами функции f. »мпликанты g1, g2, g4, g6 не €вл€ютс€ простыми, так как их части €вл€ютс€ импликантами функции f, например g5 €вл€етс€ частью g1. ѕриведем без доказательства два утверждени€, полезные при получении минимальной ƒЌ‘.
, €вл€ютс€ простыми импликантами функции f. »мпликанты g1, g2, g4, g6 не €вл€ютс€ простыми, так как их части €вл€ютс€ импликантами функции f, например g5 €вл€етс€ частью g1. ѕриведем без доказательства два утверждени€, полезные при получении минимальной ƒЌ‘.
|
|
|
1. ƒизъюнкци€ любого числа импликант булевой функции f также €вл€етс€ импликантой этой функции.
2. Ћюба€ булева функци€ f эквивалентна дизъюнкции всех своих простых импликант. “ака€ форма представлени€ булевой функции называетс€ сокращенной ƒЌ‘.
ѕеребор всех возможных импликант дл€ булевой функции f из рассмотренного примера дает возможность убедитьс€, что простых импликант всего две: g3 и g5.—ледовательно, сокращенна€ ƒЌ‘ функции f имеет вид:
 .
.
ак видно из табл. 1, импликанты g3,, g5 в совокупности покрывают своими единицами все единицы функции f. ѕолучение сокращенных ƒЌ‘ €вл€етс€ первым этапом отыскани€ минимальных форм булевых функций. ак уже отмечалось, в сокращенную ƒЌ‘ вход€т все простые импликанты булевой функции. »ногда из сокращенной ƒЌ‘ можно убрать одну или несколько простых импликант, не наруша€ эквивалентности исходной функции. “акие простые импликанты назовем лишними. »сключение лишних простых импликант из сокращенных ƒЌ‘ Ч второй этап минимизации.
ќпределение. —окращенна€ ƒЌ‘ булевой функции называетс€ тупиковой, если в ней отсутствуют лишние простые импликанты.
”странение лишних простых импликант из сокращенной ƒЌ‘ булевой функции не €вл€етс€ однозначным процессом, т. е. булева функци€ может иметь несколько тупиковых ƒЌ‘.
”тверждение. “упиковые ƒЌ‘ булевой функции f, содержащие минимальное число букв, €вл€ютс€ минимальными. ћинимальных ƒЌ‘ тоже может быть несколько.
–ассмотрим несколько методов минимизации. ¬се они практически различаютс€ лишь на первом этапе Ч этапе получени€ сокращенной ƒЌ‘. —ледует отметить, что, к сожалению, поиск минимальной ƒЌ‘ всегда св€зан с некоторым перебором решений. —уществуют методы уменьшени€ этого перебора, однако он всегда остаетс€.
ћетод вайна
ћетод вайна основываетс€ на применении двух основных соотношений.
1. —оотношение склеивани€
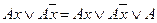 ,
,
где ј Ч любое элементарное произведение.
2. —оотношение поглощени€
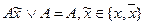 .
.
| “аблица 2 | ||||
| x1 | x2 | x3 | x4 | f |
—праведливость обоих соотношений легко провер€етс€. —уть метода заключаетс€ в последовательном выполнении всех возможных склеивании и затем всех поглощений, что приводит к сокращенной ƒЌ‘. ћетод применим к совершенной ƒЌ‘. »з соотношени€ поглощени€ следует, что произвольное элементарное произведение поглощаетс€ любой его частью.
ƒл€ доказательства достаточно показать, что произвольна€ проста€ импликанта 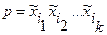 может быть получена. ¬ самом деле, примен€€ к р операцию развертывани€ (обратную операции склеивани€):
может быть получена. ¬ самом деле, примен€€ к р операцию развертывани€ (обратную операции склеивани€):
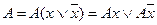
по всем недостающим переменным 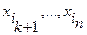 исходной функции f, получаем совокупность S конституент единицы. ѕри склеивании всех конституент из S получим импликанту р. ѕоследнее очевидно, поскольку операци€ склеивани€ обратна операции развертывани€. ћножество S конституент об€зательно присутствует в совершенной ƒЌ‘ функции f поскольку р Ч ее импликанта.
исходной функции f, получаем совокупность S конституент единицы. ѕри склеивании всех конституент из S получим импликанту р. ѕоследнее очевидно, поскольку операци€ склеивани€ обратна операции развертывани€. ћножество S конституент об€зательно присутствует в совершенной ƒЌ‘ функции f поскольку р Ч ее импликанта.
|
|
|
ѕример. ѕусть имеетс€ булева функци€, заданна€ таблицей истинности (табл. 9.12). ≈е —ƒЌ‘ имеет вид:
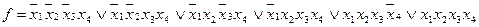
ƒл€ удобства изложени€ пометим каждую конституенту единицы из —ƒЌ‘ функции f каким-либо дес€тичным номером (произвольно). ¬ыполн€ем склеивани€. онституента 1 склеиваетс€ только с конституентой 2 (по переменной  ) и с конституентой 3 (по переменной
) и с конституентой 3 (по переменной  ), конституента 2 с конституентой 4 и т. д.
), конституента 2 с конституентой 4 и т. д.
¬ результате получаем
1Ч2: 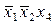
1Ч3: 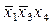
2Ч4: 
3Ч4: 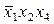
4Ч6: 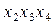
5Ч6: 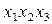
«аметим, что результатом склеивани€ €вл€етс€ всегда элементарное произве≠дение, представл€ющее собой общую часть склеиваемых конституент.
ƒалее производим склеивани€ получаемых элементарных произведений. —клеиваютс€ только те произведени€, которые содержат одинаковые переменные. »меет место два случа€ склеивани€:
 ;
;
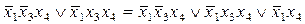 ,
,
с по€влением одного и того же элементарного произведени€ 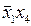 ƒальнейшие склеи≠вани€ невозможны. ѕроизвед€ поглощени€ (из полученной ƒЌ‘ вычеркиваем все поглощаемые элементарные произведени€), получим сокращенную ƒЌ‘:
ƒальнейшие склеи≠вани€ невозможны. ѕроизвед€ поглощени€ (из полученной ƒЌ‘ вычеркиваем все поглощаемые элементарные произведени€), получим сокращенную ƒЌ‘:
.
ѕереходим ко второму этапу. ƒл€ получени€ минимальной ƒЌ‘ необходимо убрать из сокращенной ƒЌ‘ все лишние простые импликанты. Ёто делаетс€ с помощью специальной импликантной матрицы вайна. —троки такой матрицы отмечаютс€ простыми импликантами булевой функции, т. е. членами сокращенной ƒЌ‘, а столбцы Ч конституентами единицы, т. е. членами —ƒЌ‘ булевой функции.
ѕример (продолжение). »мпликантна€ матрица имеет вид (табл. 3).
ак уже отмечалось, проста€ импликанта поглощает некоторую конституенту единицы, если €вл€етс€ ее собственной частью. —оот≠ветствующа€ клетка импликантной матрицы на пересечении строки (с рассматриваемой простой импликантой) и столбца (с конституентой единицы) отмечаетс€ крестиком (табл. 3). ћинимальные ƒЌ‘ стро€тс€ по импликантной матрице следующим образом:
1) ищутс€ столбцы импликантной матрицы, имеющие только один крестик. —оответствующие этим крестикам простые импликанты называютс€ базисными и составл€ют так называемое €дро булевой функции. ядро об€зательно входит в минимальную ƒЌ‘.
2) рассматриваютс€ различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столб≠цы импликантной матрицы, и выбираютс€ варианты с
минимальным суммарным числом букв в такой совокупности импликант.
| “аблица 3 | ||||||
| ѕростые »мпликанты | онституенты единицы | |||||
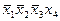
| 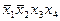
| 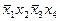
| 
| 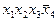
| 
| |
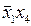
| x | x | x | x | ||

| x | x | ||||
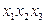
| x | x |
ѕример (продолжение). ядром нашей функции €вл€ютс€ импликанты  ;
; 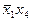 .»мпликанта
.»мпликанта  Ч лишн€€, так как €дро накрывает все столбцы импликант≠ной матрицы. ѕоэтому функци€ имеет единственную тупиковую и минимальную ƒЌ‘:
Ч лишн€€, так как €дро накрывает все столбцы импликант≠ной матрицы. ѕоэтому функци€ имеет единственную тупиковую и минимальную ƒЌ‘:
f = 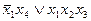 .
.
—ледует отметить, что число N крестиков в одной строке всегда €вл€етс€ степенью 2. Ѕолее того, читатель может легко убедитьс€ в том, что
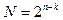 ,где k Ч число букв, содержащихс€ в простой импликанте.
,где k Ч число букв, содержащихс€ в простой импликанте.
«аметим также, что использу€ различные соотношени€, можно расширить"область применени€ метода вайна за пределы совершенной ƒЌ‘.
ѕример. ћинимизировать булеву функцию f методом вайна:
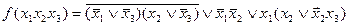 .
.
1. »збавл€емс€ от отрицаний и скобок, использу€ приведенные соотношени€
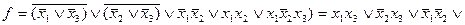
2. ¬осстанавливаем —ƒЌ‘ функции f, примен€€ операцию развертывани€
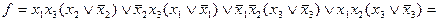
 .
.
3. Ќайдем сокращенную ƒЌ‘ функции f, производ€ в —ƒЌ‘ все возможные склеивани€
 .
.
4. »щем минимальную ƒЌ‘ функции f по импликантной матрице (табл. 4). ядро булевой функции:  ,
, 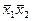 .ћинимальные ƒЌ‘:
.ћинимальные ƒЌ‘:
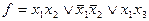 ;
;
 .
.
| “аблица 4 | ||||||
| ѕростые импликанты системы функций | онституенты единицы функции 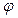
| |||||
| x1x2x3 | 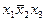
| 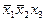
| 
| 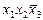
| ||
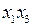
| x | x | ||||
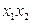
| x | x | ||||

| x | x | ||||

| x | x |
|
|
|






