УДК:004.451:004.43
ТОЧНОСТЬ ВЫЧИСЛЕНИЙ В КОМПЬЮТЕРНОЙ АРИФМЕТИКЕ
Люлюзов Малик Юсупович, магистрант 2-го курса направления 710400 «Программная инженерия», кафедра «Программное обеспечение компьютерныхсистем» (ПОКС), КГТУ им. И. Раззакова, (+996) 772-66-93-32. г.Бишкек, пр. Мира 66, e-mail: abdu.malik5660@gmail.com.
Тен Иосиф Григорьевич, к.т.н., профессор, заведующий кафедрой ПОКС, КГТУ им. И. Раззакова, (+996) 543-71-26-37. г.Бишкек, пр. Мира 66, e-mail: tenig@mail.ru.
Мусина Индира Рафиковна, к.т.н., доцент кафедры ПОКС, КГТУ им. И.Раззакова, (+996) 555-00-58-98. 720044, г.Бишкек, пр. Мира - 66, e-mail: musina-indira@yandex.ru
Аннотация
В данной статье описывается разработка программы, формирующая множество чисел, с которыми в компьютере оперирует любая программа. Данная программа генерирует систему чисел с плавающей запятой для наглядной демонстрации арифметических систем ограниченной разрядности. Это поможет дать студенту четкое и ясное знание о том, какими числами может оперировать любая компьютерная программа. В статье приведено техническое задание и руководство к разработке подобной программы студентами младших курсов.
Ключевые слов а: компьютерная арифметика, точность вычислений, разрядность процессора, система числа с плавающей запятой.
FINITE-PRECISION ARITHMETIC SYSTEMS
Malik Usupovich Luluzov, First-year master student of Software Engineering (SE) Department, Kyrgyz State Technical University (KSTU) named after I. Razzakov, (+996) 56-38-53. 720044,Bishkek city, 66, prospect Mira, e-mail: abdu.malik5660@gmail.com.
Iosif Grigorievich Ten, PhD, Professor, Head of SE Department, KSTU, named after I. Razzakov, (+996) 56-38-53. 720044, Bishkek city, 66, prospect Mira, e-mail: tenig@mail.ru.
Musina Indira Rafikovna, PhD, Associate Professor, SE Department, (+996) 56-38-53. 720044, Bishkek city, KSTU named after I.Razzakov e-mail: musina-indira@yandex.ru.
Summary
This article describes the development of a program that generates a set of numbers, which operates any computer program. The program generates a system of floating-point arithmetic to illustrate the limited bit systems. This will give the student a clear and precise knowledge about what numbers can operate any computer program. Software requirements specifications and guidance for development of similar program by junior students are described in the article.
Keywords: computer arithmetic, calculation accuracy, bit processor, a floating point number systems.
ВВЕДЕНИЕ
На сегодняшний день при решении любой задачи, требующей арифметических вычислений на компьютере, пользователь сталкивается с двумя видами ошибок: ошибки входных данных (ошибки действий пользователя) и ошибки вычислений. И если на первый вид ошибок разработчики программ никак повлиять не могут, то ответственность за появление ошибок второго вида полностью возлагается на них. Данная статья посвящена решению проблемы, связанной именно с ошибками вычислений.
Если исключить все ошибки разработчика программы, связанные с неверной реализацией алгоритма, то ошибки в вычислениях могут появляться из-за округления в самой системе, т.к. любая компьютерная система не может быть бесконечно точной. Причиной такого рода ошибок является ограничение памяти и разрядности процессора. К примеру, в натуральной арифметике, которую изучают в школе, между нулем и единицей существует бесконечное количество вещественных чисел, иными словами различие между двумя соседними числами в натуральной арифметике стремится к нулю. В свою очередь компьютер из-за своей ограниченной разрядности памяти может хранить и использовать только ограниченное количество чисел. От чего зависит набор этих чисел и какими характеристиками они обладают, мы рассмотрим в данной статье.
Для представления этого ограниченного набора чисел, была введена система чисел с плавающей запятой, что является компромиссом между точностью и скоростью вычислений. Число с плавающей запятой состоит из набора отдельных разрядов, условно разделенных на знак, порядок и мантиссу [2]. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой (рис. 1).
 Рис. 1. Представление числа с плавающей запятой.
Рис. 1. Представление числа с плавающей запятой.
РАЗРАБОТКА ТЕХНИЧЕСКОГО ЗАДАНИЯ НА ПРОГРАММУ
Задача состоит в разработке технического задания на компьютерную программу, генерирующую систему чисел с плавающей запятой, с целью улучшения качества обучения студентов по информатике. Обученный студент должен уметь учитывать особенности компьютерной арифметики при разработке программ, решающих вычислительные задачи, в которых требуются получать решения с предельно возможной максимальной точностью. Необходимо систему чисел с плавающей запятой наглядно и информативно представить студентам так, чтобы они поняли их особенности и учитывали эти особенности при решении своих задач. Поэтому пользовательскими требованиями к ПО являются следующее:
· Для достижения бизнес-цели разработки программы необходимо в темпе реального текущего аудиторного занятия генерировать систему чисел с плавающей запятой для наглядного представления их студентам.
· При задании одной из наиболее известных оснований системы счисления  необходимо сгенерировать систему счисления, соответствующую выбранному основанию счисления. Это означает, что программа должна продемонстрировать множество цифр, которое соответствует выбранному основанию системы счисления. Это позволит пользователю-студенту наглядно увидеть различие между понятиями основание системы счисления и самой системой счисления и закрепить в памяти эти знания. Наглядности можно достигнуть, если применить системный подход и представить основание системы счисления как входные данные, которые обрабатываются и преобразуются некоторой процедурой в множество цифр, составляющих систему счисления, как выходные данные некоторой подсистемы №1 как это представлено на рис.2.
необходимо сгенерировать систему счисления, соответствующую выбранному основанию счисления. Это означает, что программа должна продемонстрировать множество цифр, которое соответствует выбранному основанию системы счисления. Это позволит пользователю-студенту наглядно увидеть различие между понятиями основание системы счисления и самой системой счисления и закрепить в памяти эти знания. Наглядности можно достигнуть, если применить системный подход и представить основание системы счисления как входные данные, которые обрабатываются и преобразуются некоторой процедурой в множество цифр, составляющих систему счисления, как выходные данные некоторой подсистемы №1 как это представлено на рис.2.
Рис.2. Входные и выходные данные подсистемы №1.
· По заданному основанию системы счисления 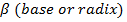 и заданной точности
и заданной точности  необходимо сгенерировать мантиссу числа с плавающей запятой. Мантисса
необходимо сгенерировать мантиссу числа с плавающей запятой. Мантисса  это строка символов, составленная из цифр, допустимых для данного основания счисления. Мантисса необходима для формирования системы чисел с плавающей запятой и представляет собой матрицу размера r*t, где
это строка символов, составленная из цифр, допустимых для данного основания счисления. Мантисса необходима для формирования системы чисел с плавающей запятой и представляет собой матрицу размера r*t, где 

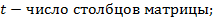
 Для понимания алгоритма генерирования системы чисел с плавающей запятой необходимо максимально наглядно представлять мантиссу, чтобы студент увидел связи между заданными основанием системы счисления
Для понимания алгоритма генерирования системы чисел с плавающей запятой необходимо максимально наглядно представлять мантиссу, чтобы студент увидел связи между заданными основанием системы счисления  и точностью
и точностью  и соответствующей этим двум параметрам мантиссой системы чисел с плавающей запятой. Наглядности можно достигнуть, если применить системный подход и представить эти два параметра
и соответствующей этим двум параметрам мантиссой системы чисел с плавающей запятой. Наглядности можно достигнуть, если применить системный подход и представить эти два параметра 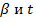 как входные данные, а мантиссу как выходные данные некоторой подсистемы №2 как это представлено на рис.3.
как входные данные, а мантиссу как выходные данные некоторой подсистемы №2 как это представлено на рис.3.
Рис.3. Входные и выходные данные подсистемы №2.
· По заданным границам области изменения экспоненты в виде соотношения  требуется сгенерировать и наглядно продемонстрировать множество возможных значений экспоненты, чтобы иметь конкретное представление о возможных значениях экспоненты. Наглядности можно достигнуть, если применить системный подход и представить эти два параметра
требуется сгенерировать и наглядно продемонстрировать множество возможных значений экспоненты, чтобы иметь конкретное представление о возможных значениях экспоненты. Наглядности можно достигнуть, если применить системный подход и представить эти два параметра 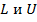 как входные данные, а множество возможных значений экспоненты
как входные данные, а множество возможных значений экспоненты  как выходные данные некоторой подсистемы №3 как это представлено на рис.4.
как выходные данные некоторой подсистемы №3 как это представлено на рис.4.
Рис.4. Входные и выходные данные подсистемы №3.
· Необходимо графически представить систему чисел с плавающей запятой компьютерной арифметики для наглядной демонстрации свойств такой системы, отличающих ее от системы чисел натуральной арифметики:
o Свойство 1: Любая система с плавающей запятой как функция имеет нижнюю 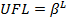 и верхнюю
и верхнюю  границы области определения значений функции (domain of function);
границы области определения значений функции (domain of function);
o Свойство 2: Любая система с плавающей запятой содержит конечное количество дискретных чисел в этих границах. Количество таких чисел определяется формулой  ;
;
o Свойство 3: Множество таких чисел неравномерно распределено в диапазоне их изменения от нижней 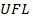 до верхней
до верхней  границы области определения значений функции (domain of function);
границы области определения значений функции (domain of function);
o Свойство 4: Поскольку в натуральной арифметике имеется бесчисленное множество чисел, тогда как в компьютерной арифметике имеется только лишь конечное количество чисел, то очевидно, что не все реальные числа натуральной арифметики можно точно представить в системе с плавающей запятой. Реальные числа, которые можно абсолютно точно представить в какой-либо заданной системе с плавающей запятой, называются иногда машинными числами (machine numbers).
o Свойство 5: В любой вычислительной задаче, в которой требуется использовать реальные (не целые) числа на компьютере, погрешность решения не может быть равна нулю и минимально достижимое значение погрешности зависит от параметров системы с плавающей запятой и характеристик самого компьютера таких как разрядность памяти компьютера (memory width) и размер машинного слова (machine/computer word or length).
Для понимания и овладения умением правильно учитывать и применять свойства системы чисел с плавающей запятой при программной реализации алгоритмов решения вычислительных задач, необходимо наглядно демонстрировать связь между параметрами системы чисел с плавающей запятой и их свойствами. Поэтому функциональными требованиями к ПО являются следующее:
· SRS1.1: Система должна дать возможность пользователю вводить набор следующих параметров, определяющих однозначно конкретную систему чисел с плавающей запятой:
· b- base or radix -основание системы счисления;
· βt - Precision -точность;
· [L,U]-Exponent Range -диапазон изменения экспоненты e;
L - Lower point of the Exponent Range - нижняя граница диапазона изменения экспоненты e;
U - Upper point of the Exponent Range -верхняя граница диапазона изменения экспоненты e;
SRS - Software Requirements Specification - эта аббревиатура означает "Спецификация требований к ПО".
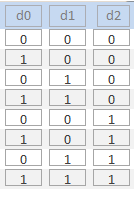
· SRS1.2: Система для заданного основания системы счисления ( должна иметь возможность генерировать и демонстрировать саму эту систему счисления, то есть определенный набор цифр, составляющих эту систему. На рис.5 приведены примеры алгоритма формирования системы счисления компьютерной арифметики для наиболее известных оснований системы счисления такие как двоичное, восьмеричное, десятичное и шестнадцатеричное.
должна иметь возможность генерировать и демонстрировать саму эту систему счисления, то есть определенный набор цифр, составляющих эту систему. На рис.5 приведены примеры алгоритма формирования системы счисления компьютерной арифметики для наиболее известных оснований системы счисления такие как двоичное, восьмеричное, десятичное и шестнадцатеричное.
Рис.5. Алгоритм формирования системы счисления компьютерной арифметики по основаниям 2, 8, 10 и 16.
· SRS1.3: Система должна для заданного основания системы счисления  и (base or radix) заданной точности
и (base or radix) заданной точности 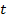 генерировать и демонстрировать множество мантисс числа с плавающей запятой. Мантисса
генерировать и демонстрировать множество мантисс числа с плавающей запятой. Мантисса 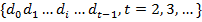 - это прямоугольная матрица D(r х t), где r=β^t - число строк матрицы, а t- число столбцов,где строки такой матрицы составлены из всевозможных сочетаний цифр
- это прямоугольная матрица D(r х t), где r=β^t - число строк матрицы, а t- число столбцов,где строки такой матрицы составлены из всевозможных сочетаний цифр  , допустимых для данного основания счисления (
, допустимых для данного основания счисления ( . На рисунках 6 и 7 приведены примеры мантисс для двух систем чисел с плавающей запятой при значениях параметров
. На рисунках 6 и 7 приведены примеры мантисс для двух систем чисел с плавающей запятой при значениях параметров 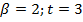 и
и 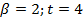 соответственно.
соответственно.
Мантисса  с плавающей запятой при с плавающей запятой при 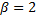 и и  представляет собой матрицу представляет собой матрицу  размера (8X3) и имеет следующий вид: размера (8X3) и имеет следующий вид:
| 
|
Рис.6. Мантисса 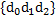 при
при 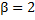 и
и 
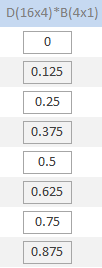
Мантисса 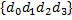 числа с плавающей запятой при числа с плавающей запятой при 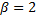 и и  представляет собой матрицу представляет собой матрицу  размера (16X4) и имеет следующий вид: размера (16X4) и имеет следующий вид:
| 
|
Рис.7: Мантисса 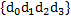 числа с плавающей запятой при
числа с плавающей запятой при 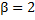 и
и 
· SRS1.4: Система должна для заданного основания системы счисления  и заданной точности
и заданной точности  генерировать и демонстрировать вектор
генерировать и демонстрировать вектор  размера
размера 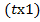 . На рисунках 8 и 9 приведены примеры такого вектора
. На рисунках 8 и 9 приведены примеры такого вектора 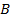 для числа с плавающей запятой при значениях параметров
для числа с плавающей запятой при значениях параметров 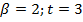 и
и 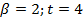 соответственно.
соответственно.
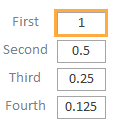
Вектор 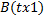 вида вида 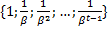 имеет размер имеет размер 
| 
|
Рис.8. Вектор размера 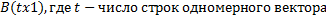 вида
вида 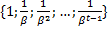 для числа с плавающей запятой при значениях параметров
для числа с плавающей запятой при значениях параметров  .
.
Вектор 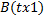 вида вида 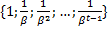 имеет размер имеет размер 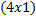
| 
|
Рис.9. Вектор размера B(tx1), где t-число строк одномерного вектора вида 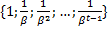 для числа с плавающей запятой при значениях параметров
для числа с плавающей запятой при значениях параметров  .
.
· SRS1.5: Система должна иметь возможность для заданного основания системы счисления  и заданной точности
и заданной точности  генерировать мантиссу числа с плавающей запятой в виде матрицы
генерировать мантиссу числа с плавающей запятой в виде матрицы  и умножить эту матрицу на одномерный вектор
и умножить эту матрицу на одномерный вектор 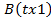 и демонстрировать в упорядоченном виде полученный числовой вектор
и демонстрировать в упорядоченном виде полученный числовой вектор 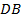 размера
размера 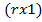 . На рисунках 10 и 11 приведены в виде примера результаты умножения матрицы
. На рисунках 10 и 11 приведены в виде примера результаты умножения матрицы  и вектора
и вектора  для системы чисел с плавающей запятой при значениях параметров
для системы чисел с плавающей запятой при значениях параметров 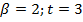 и
и 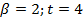 соответственно. Результат вычисления представляет собой вектор
соответственно. Результат вычисления представляет собой вектор 
Произведение мантиссы 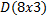 числа с плавающей запятой и вектора числа с плавающей запятой и вектора 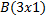 представляет вектор размера представляет вектор размера 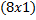
| 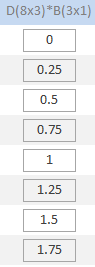
|
Рис.10. Произведение мантиссы  числа с плавающей запятой на вектор
числа с плавающей запятой на вектор 
при значениях параметров  .
.
Произведение мантиссы 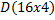 числа с плавающей запятой и вектора числа с плавающей запятой и вектора  представляет вектор размера представляет вектор размера 
|  
|
Рис.11. Произведение мантиссы  числа с плавающей запятой на вектор
числа с плавающей запятой на вектор 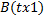 при значениях параметров
при значениях параметров  .
.
· SRS1.6: Система должна иметь возможность для заданного основания системы счисления  заданной точности
заданной точности  и для заданного диапазона изменения экспоненты
и для заданного диапазона изменения экспоненты  умножить вектор
умножить вектор  на число
на число 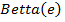 при всех возможных значениях экспоненты
при всех возможных значениях экспоненты 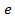 . То есть требуется вычислить выражение
. То есть требуется вычислить выражение  которое будет представлять набор такого количества векторов
которое будет представлять набор такого количества векторов  сколько имеется значений экспоненты. В результате будет получен полный набор чисел в количестве
сколько имеется значений экспоненты. В результате будет получен полный набор чисел в количестве  Если среди этих чисел будут одинаковые числа, то требуется сформировать новый набор чисел только из чисел, отличающихся друг от друга по значению и продемонстрировать полученный числовой вектор. На рисунках 12 и 13 приведены в виде примера полные результаты такого умножения для системы чисел с плавающей запятой при значениях параметров
Если среди этих чисел будут одинаковые числа, то требуется сформировать новый набор чисел только из чисел, отличающихся друг от друга по значению и продемонстрировать полученный числовой вектор. На рисунках 12 и 13 приведены в виде примера полные результаты такого умножения для системы чисел с плавающей запятой при значениях параметров 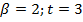 и
и 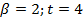 соответсвенно. В результате будет получен полный набор чисел в количестве 24 и 48 соответственно. На рисунках 14 и 15 приведены в виде примера результаты такого умножения с группировкой для системы чисел с плавающей запятой при значениях параметров
соответсвенно. В результате будет получен полный набор чисел в количестве 24 и 48 соответственно. На рисунках 14 и 15 приведены в виде примера результаты такого умножения с группировкой для системы чисел с плавающей запятой при значениях параметров 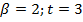 и
и 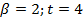 соответственно. В результате будет получен усеченный набор чисел в количестве 16 и 32 соответственно.
соответственно. В результате будет получен усеченный набор чисел в количестве 16 и 32 соответственно.
Результат умножения произведения мантиссы числа с плавающей запятой  и вектора и вектора  на числа вида Betta(e),для всех e в диапазоне L≤e≤U представляет набор чисел с плавающей запятой в количестве на числа вида Betta(e),для всех e в диапазоне L≤e≤U представляет набор чисел с плавающей запятой в количестве 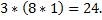
|  
|
Рис.12. Результат умножения произведения мантиссы 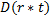 числа с плавающей запятой и вектора
числа с плавающей запятой и вектора  на число вида
на число вида  при значениях параметров
при значениях параметров 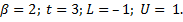
Результат умножения произведения мантиссы числа с плавающей запятой  и вектора и вектора  на число вида на число вида  представляет набор чисел с плавающей запятой в количестве представляет набор чисел с плавающей запятой в количестве 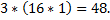
|    
|
Рис.13. Результат умножения произведения мантиссы 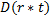 числа с плавающей запятой и вектора
числа с плавающей запятой и вектора  на число вида
на число вида  при значениях параметров
при значениях параметров 
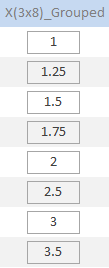
Результат умножения произведения мантиссы числа с плавающей запятой  и вектора и вектора  на числа вида Betta(e), для всех e в диапазоне L≤e≤U с группировкой представляет набор чисел с плавающей запятой в количестве на числа вида Betta(e), для всех e в диапазоне L≤e≤U с группировкой представляет набор чисел с плавающей запятой в количестве 
|  
|
Рис.14. Результат умножения произведения мантиссы 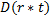 числа с плавающей запятой и вектора
числа с плавающей запятой и вектора  на число вида
на число вида  при значениях параметров
при значениях параметров  с группировкой.
с группировкой.
Результат умножения произведения мантиссы числа с плавающей запятой  и вектора и вектора  на число вида на число вида  с группировкой представляет набор чисел с плавающей запятой в количестве с группировкой представляет набор чисел с плавающей запятой в количестве 
|    
|
Рис.15. Результат умножения произведения мантиссы 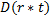 числа с плавающей запятой и вектора
числа с плавающей запятой и вектора  на число вида
на число вида  при значениях параметров
при значениях параметров 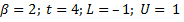 с группировкой.
с группировкой.
· SRS1.7: Система должна из множества чисел 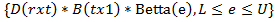 , которое можно описать в более развернутом виде: {x}={DB(rx1)*Betta(L),DB(rx1)*Betta(L+1),…,DB(rx1)*Betta(U-1),DB(rx1)*Betta(U)} сформировать новое множество
, которое можно описать в более развернутом виде: {x}={DB(rx1)*Betta(L),DB(rx1)*Betta(L+1),…,DB(rx1)*Betta(U-1),DB(rx1)*Betta(U)} сформировать новое множество  чисел, которое удовлетворяет условию
чисел, которое удовлетворяет условию  и продемонстрировать полученный числовой вектор. На рисунках 16 и 17 приведены в виде примера множество чисел с плавающей запятой при значениях параметров
и продемонстрировать полученный числовой вектор. На рисунках 16 и 17 приведены в виде примера множество чисел с плавающей запятой при значениях параметров 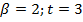 и
и 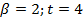 соответственно. Это множество
соответственно. Это множество  чисел состоит только из положительных чисел, находящихся в диапазоне
чисел состоит только из положительных чисел, находящихся в диапазоне  .
.
· Результат применения операции 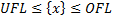 к множеству чисел к множеству чисел  представляет новое множество представляет новое множество  из 12 чисел с плавающей запятой, так как из 12 чисел с плавающей запятой, так как 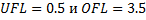
|  
|
Рис.16. Результат применения операции 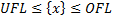 при значениях параметров
при значениях параметров
 =2; t=3;L= –1; U= 1.
=2; t=3;L= –1; U= 1.
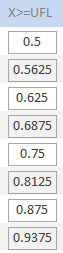
Результат применения операции 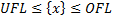 к множеству чисел к множеству чисел 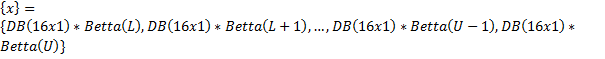 представляет новое множество представляет новое множество  из 24 чисел с плавающей запятой, так как из 24 чисел с плавающей запятой, так как 
|   
|
Рис.17. Результат применения операции 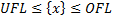 при значениях параметров
при значениях параметров
β=2; t=4;L= –1; U= 1
· SRS1.8: Система должна из множества  чисел, которое удовлетворяет условию
чисел, которое удовлетворяет условию  сформировать точно такое же количество отрицательных чисел и продемонстрировать полученный числовой вектор. На Рисунках рисунках 18 и 19 приведены в виде примера множество чисел с плавающей запятой при значениях параметров
сформировать точно такое же количество отрицательных чисел и продемонстрировать полученный числовой вектор. На Рисунках рисунках 18 и 19 приведены в виде примера множество чисел с плавающей запятой при значениях параметров 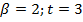 и
и 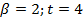 соответственно. Это множество
соответственно. Это множество  чисел состоит только из отрицательных чисел, находящихся в диапазоне
чисел состоит только из отрицательных чисел, находящихся в диапазоне 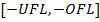 .
.
Результат применения операции умножения (–1) к каждому числу из множества 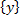 представляет новое множество представляет новое множество 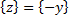 из 12 отрицательных чисел с плавающей запятой из 12 отрицательных чисел с плавающей запятой
|  
|
Рис.18. Результат применения операции  при значениях параметров
при значениях параметров
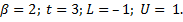
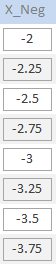
Результат применения операции умножения (–1) к каждому числу из множества 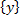 представляет новое множество представляет новое множество 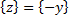 из 24 отрицательных чисел с плавающей запятой из 24 отрицательных чисел с плавающей запятой
|   
|
Рис.19. Результат применения операции  при значениях параметров
при значениях параметров

· SRS1.9: Система должна к множеству  чисел, которое удовлетворяет условию
чисел, которое удовлетворяет условию 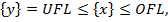 добавить множество чисел
добавить множество чисел  и добавить к этому объединенному множеству еще число ноль, и продемонстрировать полученное множество чисел. Это множество чисел и представляет собой результирующую/требуемую систему чисел с плавающей запятой, соответствующую заданному набору входных параметров
и добавить к этому объединенному множеству еще число ноль, и продемонстрировать полученное множество чисел. Это множество чисел и представляет собой результирующую/требуемую систему чисел с плавающей запятой, соответствующую заданному набору входных параметров  . Количество таких чисел определяется формулой
. Количество таких чисел определяется формулой 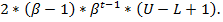 Валидность этой формулы легко проверить. Цифра 2 связана с тем, что имеется два знака числа, составляющая
Валидность этой формулы легко проверить. Цифра 2 связана с тем, что имеется два знака числа, составляющая 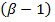 свзана с тем, что это возможное количество значений первой цифры мантиссы
свзана с тем, что это возможное количество значений первой цифры мантиссы 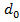 , составляющая
, составляющая 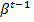 связана с тем, что каждая составляющая мантиссы числа с плавающей запятой
связана с тем, что каждая составляющая мантиссы числа с плавающей запятой 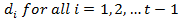 имеет возможность принимать
имеет возможность принимать 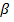 значений в диапазоне
значений в диапазоне  составляющая
составляющая  связана с тем, что экспонента e
связана с тем, что экспонента e  имеет возможность принимать такое количество значений в диапазоне
имеет возможность принимать такое количество значений в диапазоне 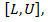 а единица в формуле добавлена, чтобы учесть цифру ноль. На рисунках 20 и 21 приведены в виде примера множество чисел с плавающей запятой при значениях параметров
а единица в формуле добавлена, чтобы учесть цифру ноль. На рисунках 20 и 21 приведены в виде примера множество чисел с плавающей запятой при значениях параметров 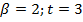 и
и 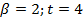 соответственно.
соответственно.
· Результат применения операции умножения (–1) к каждому числу из множества 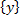 представляет новое множество представляет новое множество 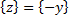 из 12 отрицательных чисел с плавающей запятой из 12 отрицательных чисел с плавающей запятой
|  
|
Рис.20. Результат применения операции  при значениях параметров
при значениях параметров
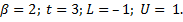
Результат применения операции умножения (–1) к каждому числу из множества 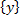 представляет новое множество представляет новое множество 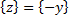 из 24 отрицательных чисел с плавающей запятой из 24 отрицательных чисел с плавающей запятой
|   
|
Рис. 21. Результат применения операции  при значениях параметров
при значениях параметров

· SRS1.10: Система должна иметь возможность графически представлять систему чисел с плавающей запятой для наглядной демонстрации свойств и особенностей такой системы, отличающих ее от системы чисел натуральной арифметики. На рисунках 22 и 23 приведены в виде примера графики распределения множества чисел для системы с плавающей запятой при значениях параметров 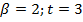 и
и 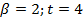 соответственно. Этот рисунок наглядно демонстрирует два главных свойства системы чисел компьютерной арифметики: во-первых, это множество чисел конечно и количество этих чисел, определяется формулой
соответственно. Этот рисунок наглядно демонстрирует два главных свойства системы чисел компьютерной арифметики: во-первых, это множество чисел конечно и количество этих чисел, определяется формулой  ; во-вторых, эти числа неравномерно распределены в диапазоне
; во-вторых, эти числа неравномерно распределены в диапазоне 

Рис. 22. График распределения множества чисел для системы с плавающей запятой при значениях параметров 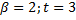 ; L= –1; U=1; Eps=0.125.
; L= –1; U=1; Eps=0.125.

Рис. 23. График распределения множества чисел для системы с плавающей запятой при значениях параметров  ; L= –1; U=1; Eps=0.0625.
; L= –1; U=1; Eps=0.0625.
ЗАКЛЮЧЕНИЕ
Были проведены исследования в области компьютерной арифметики, выявлены основные проблемы при формировании технического задания на прикладную программу, предназначенную для решения вычислительных задач. На основе этого анализа была разработана программа, которая наглядно демонстрирует зависимость точности от разрядности процессора. С помощью данной программы можно наглядно продемонстрировать эту зависимость, что позволит дать студенту четкое и ясное представление о компьютерной арифметике и числах, которые хранятся и вычисляются в компьютере. Так же в статье приведено подробное описание процесса разработки данной программы, которая позволит создать подобную программу даже студентам младших курсов.
ЛИТЕРАТУРА
1. Heath M.T. Scientific Computing. An Introductory Survey. Boston McGraw Hill, 1997 ISBN 0-07-027684-6.
2. IEEE 754 - стандарт двоичной арифметики с плавающей точкой. http://www.softelectro.ru/ieee754.html.
3. Wiegers K., Beatty J. Software Requirements. Third Edition. Redmond. Microsoft Press of Microsoft Corporation: Karl Wiegers and Seilevel, 2013. – 673 pages. ISBN: 978-0-7356-7966-5
REFERENCES
1. Heath M.T. Scientific Computing. An Introductory Survey. Boston McGraw Hill, 1997 ISBN 0-07-027684-6.






