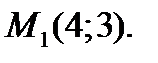Вопросы к экзамену по высшей математике.
1 курс. ИЭФ. Лектор Якименко А.А.
1. Функции одной переменной. Элементарные функции.
2. Предел функции в точке.
3. Бесконечно малые и бесконечно большие функции.
4. Основные теоремы о пределах.
5. Первый и второй замечательные пределы.
6. Сравнение бесконечно малых. Эквивалентные бесконечно малые функции.
7. Непрерывность функции в точке. Точки разрыва.
8. Основные теоремы о непрерывных функциях.
9. Производная, её геометрический, механический и экономический смысл.
10. Правила дифференцирования. Таблица производных основных элементарных функций.
11. Производная сложной, обратной и неявно заданной функции.
12. Логарифмическое дифференцирование. Применение производной в экономике.
13. Производные высших порядков.
14. Дифференциал функции, его свойства и геометрический смысл.
15. Основные теоремы о дифференцируемых на отрезке функциях. Правило Бернулли-Лопиталя.
16. Условия возрастания и убывания дифференцируемых функций. Необходимые и достаточные условия экстремума.
17. Выпуклость и вогнутость графика функции. Точки перегиба.
18. Асимптоты графика функции.
19. Общая схема исследования функции и построения её графика.
20. Наибольшее и наименьшее значения функции на отрезке.
21. Матрицы и действия над ними.
22. Определители и их свойства.
23. Обратная матрица. Ранг матрицы.
24. Общая теория систем линейных алгебраических уравнений. Теорема Кронекера-Капелли.
25. Теорема Кронекера-Капелли. Метод Гаусса решения систем линейных алгебраических уравнений.
26. Решение систем линейных алгебраических уравнений с помощью обратной матрицы. Правила Крамера.
27. Однородные системы линейных алгебраических уравнений.
28. Векторное пространство. Размерность и базис векторного пространства.
29. Основные задачи аналитической геометрии на плоскости. Прямая линия на плоскости.
30. Прямая и плоскость в пространстве.
31. Кривые второго порядка. Окружность и эллипс.
32. Кривые второго порядка. Гипербола и парабола.
33. Функции нескольких переменных. Область определения. Линии уровня.
34. Частные производные функции нескольких переменных. Частная эластичность.
35. Полный дифференциал функции нескольких переменных.
36. Производные высших порядков функции нескольких переменных.
37. Функции нескольких переменных. Производная по направлению и градиент.
38. Экстремум функции нескольких переменных. Необходимое, достаточное условия.
Тренировочные практические задания к экзамену
1. Вычислить пределы:
а)  : б)
: б)  : в)
: в) 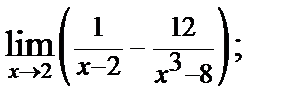
г)  д)
д) 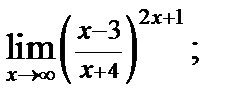 е)
е) 
2. Найти точки разрыва функции  если они существуют, и опреде-
если они существуют, и опреде-
лить их тип. Сделать схематический чертеж.

3. Вычислить производную функции 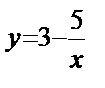 по определению.
по определению.
4. Найти  , если
, если 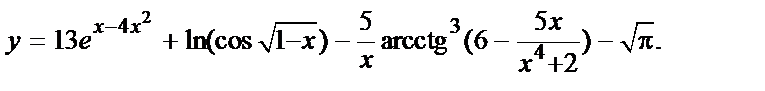
5. Найти: а)  ; б)
; б)  в)
в) 
6. Проверить, удовлетворяет ли функция  уравнению
уравнению

7. В какой точке кривой  касательная параллельна прямой
касательная параллельна прямой
 Записать уравнение касательной. Сделать чертеж.
Записать уравнение касательной. Сделать чертеж.
8. Найти 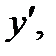 если: а)
если: а)  б)
б) 
9. Найти пределы по правилу Лопиталя:
а)  ; б)
; б) 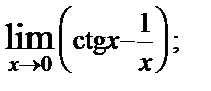 в)
в) 
10. Найти наибольшее и наименьшее значение функции  на
на
отрезке 
11. Исследовать функции методами дифференциального исчисления и постро-
ить их графики:
а)  б)
б) 
12. Даны матрицы:
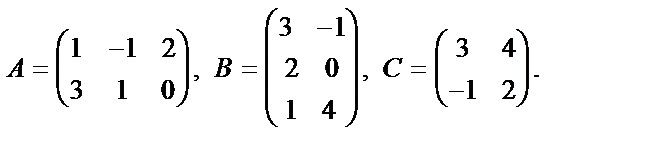
Найти: а) АВ; б)  ; в)
; в) 
13. Вычислить определитель  .
.
14. Проверить совместность системы уравнений
 ,
,
и в случае совместности решить ее: а)по формулам Крамера; б) методом
Гаусса.
15. Найти значения  , при которых векторы
, при которых векторы  и
и  коллинеарны, если
коллинеарны, если
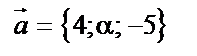 ,
, 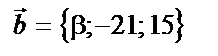 . Установить, имеют ли векторы одинаковое
. Установить, имеют ли векторы одинаковое
на правление.
16. Даны точки  Найти: а) угол
Найти: а) угол  б) пло-
б) пло-
щадь треугольника 
17. Даны векторы 

 Найти:
Найти:
а) скалярное произведение векторов  и
и 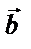 ;
;
б) вектор, перпендикулярный векторам  и
и  ;
;
в) объем параллелепипеда, построенного на векторах  ,
,  и
и  ;
;
г) векторное произведение векторов 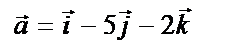 и
и 
18. Написать уравнение прямой, проходящей через точку  :
:
а) параллельно прямой 
б) перпендикулярно прямой 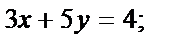
в) и точку 
г) параллельно прямой 
д) параллельно прямой 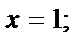
е) и начало координат.
19. Построить кривые по заданным уравнениям:
а) 
б) 
в) 
г) 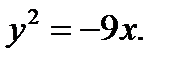
20. Найти частные производные функции:
а)  б)
б) 
в)  ; г)
; г) 
21. Показать, что если  то
то 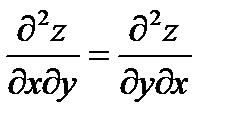 .
.
22. Найти grad u в точке А, если:
а) 
б) 
23. Найти производную функции  в точке
в точке  по направле -
по направле -
нию вектора 
24. Найти локальные экстремумы функции:
а) 
б) 
25. Найти производную функции 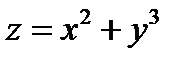 в точке
в точке  по направле-
по направле-
нию вектора 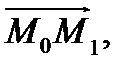 если
если