Максимальная поперечная сила на опоре от расчетных нагрузок составит:
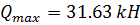
Проверим необходимость постановки расчетной поперечной арматуры в лобовом ребре из условий:
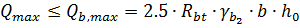 ;
;
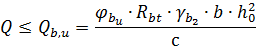
1. Определим фактическую рабочую высоту сечения при диаметре рабочих стержней 14 мм и толщине защитного слоя 20 мм.
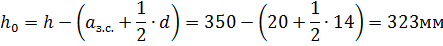
2. Определим расчетное значение нагрузки приложенной к лобовому ребру.
Часть нагрузки, действующей на лобовое ребро, приложена к полке, то есть в пределах высоты поперечного сечения, следовательно разгружающее действие распределенной нагрузки по длине наклонного сечения может быть учтено только на той части наклонного сечения, на которой эта нагрузка расположена над наклонным сечением, что учитывается при определении этой нагрузки соотношением 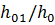 :
:
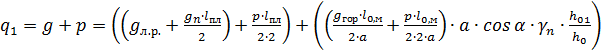 =
=
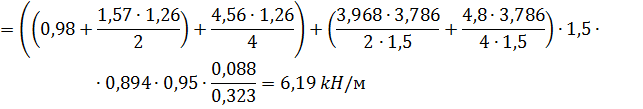
где, 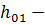 рабочая высота сечения полки лобового ребра (рис 14);
рабочая высота сечения полки лобового ребра (рис 14);
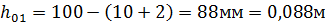
Рис 14. К определению рабочей высоты сечения полки лобового ребра
3. Определим значение 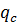 по формуле:
по формуле:
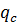 =0.16∙
=0.16∙ 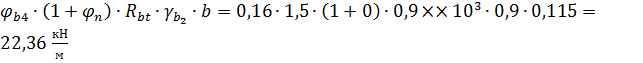
4. Проверим условие 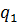 ≤
≤ 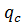 :
:
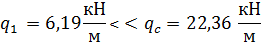
Так как условие выполняется, то длину проекции наклонного сечения с начинающегося от опоры принимаем равным:
с = 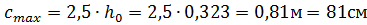
5. Определим поперечную силу в конце наклонного сечения:
Q = 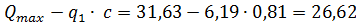 kH
kH
6. Определим максимальную поперечную силу воспринимаемую бетоном:
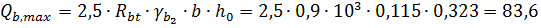 kH
kH
7. Определим значение поперечной силы 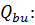
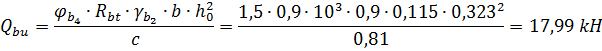
где, 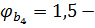 коэффициент для тяжелого бетона;
коэффициент для тяжелого бетона;
8. Проверим условие необходимости постановки поперечной арматуры по расчету:
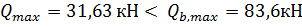
Q=26,62 кН > 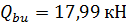
Так как одно из условий не выполняется, то поперечную арматуру подбираем по расчету.
Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине
Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине производится из условия:
Q ≤ 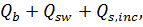
где, Q – поперечная сила в вершине наклонного сечения от действия внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения;
 поперечная сила воспринимаемая бетоном;
поперечная сила воспринимаемая бетоном;
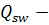 поперечная сила воспринимаемая поперечными стержнями;
поперечная сила воспринимаемая поперечными стержнями;
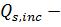 поперечная сила, воспринимаемая отгибами.
поперечная сила, воспринимаемая отгибами.
Задаемся предварительно диаметром поперечных стержней из условия их свариваемости с продольными стержнями ø14 мм и принимаем ø5 Вр-Ī с площадью 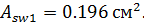 При этом площадь хомутов одной плоскости при двух каркасах n=2 cоставит
При этом площадь хомутов одной плоскости при двух каркасах n=2 cоставит 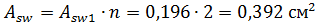
1. Определим максимальный шаг поперечных стержней:
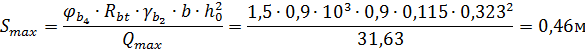
По конструктивным соображениям на приопорных участках, равных при равномерно распределенной нагрузке ¼ пролета l при высоте сечения элемента h равной или менее 450мм (h≤450мм), шаг поперечных стержней принимается не более h/2 (S ≤ h/2) и не более 150мм (S ≤ 150мм), при высоте более 450 мм (h≥450мм) шаг поперечных стержней принимается не более h/3 (S ≤ h/3) и не более 500 мм (S ≤ 500 мм). На остальной части пролета при высоте сечения h свыше 300 мм (h > 300 мм) устанавливается поперечная арматура с шагом не более (S ≤ 3h/4) и не более 500 мм (S ≤ 500 мм).
Исходя из вышеизложенного принимаем шаг поперечных стержней на приопорных участках длиной ¼l равным:
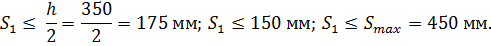
Принимаем 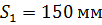 .
.
На остальной части пролета при 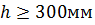 принимаем шаг равным:
принимаем шаг равным:
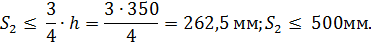
Принимаем 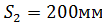
2. Определим коэффициент 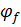 , учитывающий влияние сжатых полок в тавровых элементах по формуле:
, учитывающий влияние сжатых полок в тавровых элементах по формуле:
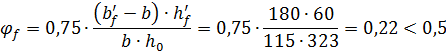
при этом, 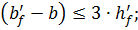 (645-115)=530мм > 3∙60=180мм
(645-115)=530мм > 3∙60=180мм
Так как условие не выполняется, принимаем 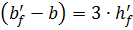 =3
=3  60=180 мм
60=180 мм
При учете свесов полок таврового сечения количество поперечной арматуры ребра должно быть не менее 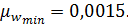
3. Проверим процент армирования:
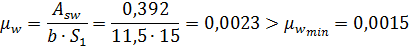
Так как условие выполняется, коэффициент 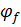 учитываем в расчете.
учитываем в расчете.
4. Определим момент, воспринимаемый бетонным сечением:
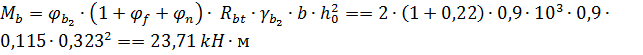 ,
,
где, 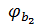 =2 - коэффициент учитывающий вид бетона;
=2 - коэффициент учитывающий вид бетона;
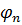 =0 - коэффициент учитывающий влияние продольных сил
=0 - коэффициент учитывающий влияние продольных сил
5. Определим погонное усилие в поперечных стержнях на единицу длины элемента по формуле:
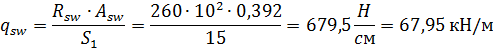
6. Определим минимальную поперечную силу воспринимаемую бетоном по формуле:
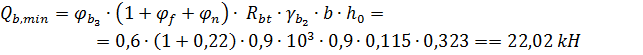
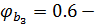 коэффициент, учитывающий вид бетона;
коэффициент, учитывающий вид бетона;
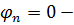 коэффициент, учитывающий влияние продольных сил
коэффициент, учитывающий влияние продольных сил
7. Определим величину 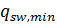 по формуле:
по формуле:
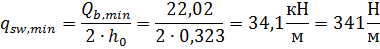
8. Проверим условие:
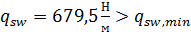 =341
=341 
Условие выполняется, величину 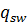 не корректируем
не корректируем
Примечание: Если 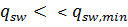 , то
, то
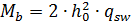 ∙
∙ 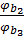 и
и 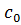 =2∙
=2∙ 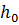
9. Определим длину проекции невыгодного наклонного сечения:
Если 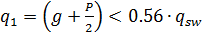 , то c =
, то c = 
Если 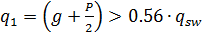 , то c =
, то c = 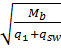
Проверим это условие и определим «c»:
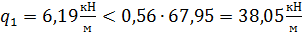 , следовательно:
, следовательно:
c = 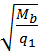 =
= 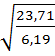 = 1.96 м;
= 1.96 м;
при этом:
с ≤ 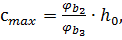
с =1,96м >  0,323 = 1,08
0,323 = 1,08
Так как условие не выполняется в расчет вводим значение с = 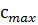 =1,08 м
=1,08 м
10. Определим длину проекции опасной наклонной трещины:
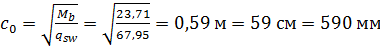 ;
;
при этом значение 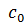 должно быть в следующих пределах:
должно быть в следующих пределах:
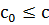 ;
; 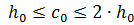 ;
;
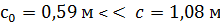
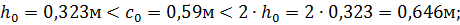
Принимаем 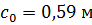
11. Определим поперечную силу воспринимаемую бетоном:
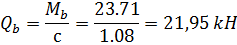
12. Проверим условие:
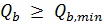
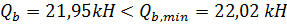
Условие не выполняется, далее в расчет вводим значение
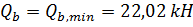
13. Определим поперечную силу воспринимаемую поперечными стержнями:
 = 67,95 ∙ 0,59 =40,1 kH
= 67,95 ∙ 0,59 =40,1 kH
14. Определим поперечную силу в конце наклонного сечения:
Q = 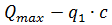 = 31,63 - 6,19 ∙ 1,08 = 24,94 kH
= 31,63 - 6,19 ∙ 1,08 = 24,94 kH
15. Проверим условие прочности наклонного сечения на действие поперечной силы по наклонной трещине:
Q = 24,94 kH < 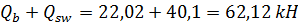
Условие выполняется, прочность наклонного сечения на действие поперечной силы обеспечена.






