Приведение силы к точке.
Пусть дана сила Р приложенная в т. С. Перенесём данную силу в заданную т. О
и уравновесим, чтобы состояние тела не изменилось.
Тогда Р = Р’ = Р”
Из т. О на линию действия силы опустим перпендикуляр
Тогда у пары сил РР’ можно найти момент М = Ра - эту
пару наз.- присоединённой.
При приведении силы Р к точке, не лежащей на линии действия силы получается
эквивалентная система, которая состоит из:
- силы равной по модулю и сонаправленную с Р
- присоединённой пары сил, момент которой равен моменту данной силы относительно точки приведения: Мо(Р) = Ра
Приведение силы к точке используют для выявления характера действия силы на тело.
Рассмотреть примеры.
Приведение плоской системы сил к данной точке.
Привести к точке можно какое угодно число сил.
В 4 разных точках приложены 4 силы Р1; Р2; Р3; Р4; приведём их в точку О
Систему сил Р1; Р2; Р3; Р4; Заменим сходящимися силами
силы Р’1; Р’2; Р’3; Р’4; приложенными в точке О и парами сил
с моментами, равными моментам заданных сил относительно
точки О: М1 = - Р1а1 = Мо(Р1) М2 = Р2а2 = Мо(Р2)
М3 = Р3а3 = Мо(Р3) М4 = Р4а4 = Мо(Р4)
Сходящиеся в точке силы можно заменить одной равнодействующей силой R’ равной
геометрической сумме составляющих сил- эту силу наз. главным вектором системы.
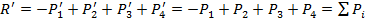
Пары сил соответственно можно заменить результирующей парой, момент которой равен
алгебраической сумме моментов заданных сил относительно точки О – этот момент наз.
главным моментом системы.
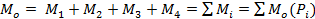
Итак: В общем случае плоская система сил в результате приведения к данной точке заме-
няется эквивалентной ей системой состоящей:
1) из одной силы – главного вектора;
2) из одной пары, момент которой наз. – главным моментом данной системы сил относи-
тельно центра приведения.
Важно: при этом главный вектор не является равнодействующей данной системы сил, т.к.
не заменяет действие системы сил, он является геометрической суммой всех сил в системе.
При приведении системы сил к точке могут быть случаи:
1) R ≠ 0; M ≠ 0 – система приводится к главному вектору и главному моменту.
2) R = 0; M ≠ 0 – система приводится к одной результирующей паре с моментом, равным
главному моменту.
3) R ≠ 0; M = 0 – система приводится к к одной равнодействующей силе, равной главному
вектору.
4) R = 0; M = 0 – система находится в равновесии.

Теорема Вариньона.
Момент равнодействующей плоской системы сил относительно произвольно взятой точки, равен алгебраической сумме моментов составляющих сил относите-льно той же точки.
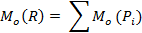
(без доказательства)
Из теоремы следует:
Главный момент плоской системы сил, относительно любой точки, лежащей на линии действия равнодействующей силы – равен 0.
Рассмотреть примеры.
Уравнения равновесия произвольной плоской системы сил.
Для равновесия системы сил, произвольно расположенных в плоскости, необхо-димо и достаточно, чтобы главный вектор и главный момент этих сил относите-
льно любого центра равнялся – 0.
R = 0 и Mo = 0.
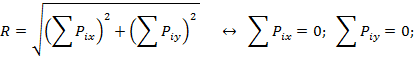
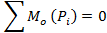
Данные уравнения равновесия произвольной плоской системы сил могут быть
представлены в трёх формах:
І основная форма: 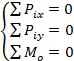
ІІ форма: 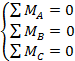
Т.к. при равновесии тела сумма моментов всех приложенных к нему сил относите-льно любой точки равна 0, то можно выбрать любые три точки (не лежащие на
одной прямой) и приравнять 0 сумму моментов относительно каждой из них.
ІІІ форма: 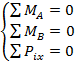
Ось ОХ не должна быть перпендикулярна линии АВ.
Рассмотреть примеры.






