Основні поняття методу скінченних різниць

Розв’язування крайових задач методом скінченних різниць

 

Методичні матеріали

до лабораторної роботи № 4 з курсу:

“Математичне моделювання в САПР”

для студентів базового напрямку

6.0804 “Комп’ютерні науки”

 

 

Затверджено

на засіданні кафедри

“Системи автоматизованого проектування”

Протокол №

від

 

 

Львів 2008

Розв’язування крайових задач методом скінченних різниць. Мето­дич­ні матеріали до лабораторної роботи № 4 з курсу: “Математичне моде­­лю­вання в САПР” для студентів базового напрямку 6.0804 “Комп’ю­тер­ні науки”.

 

 

Укладачі:

Макар В.М., доцент, к.т.н.

Юрчак І.Ю., доцент, к.т.н.

 

 

Відповідальний за випуск:

Лобур М.В., проф., д.т.н., завідувач кафедри САП

 

Рецензенти:

 

 

1. МЕТА РОБОТИ

Ознайомитися з методом скінченних різниць, способами побудови скінченно-різницевих співвідношень та отримати практичні на­вики зас­то­сування методу до розв’язання задачі Коші для зви­чайних диферен­ціаль­них рівнянь та задачі Діріхле для рівняння Лапласа.

 

ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

ОСНОВНІ ПОНЯТТЯ МЕТОДУ СКІНЧЕННИХ РІЗНИЦЬ

Розглянемо крайову задачу в області 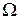з границею , записану в операторній формі:

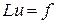, (1)

де – заданий диференціальний оператор, включаючи граничні умови, 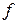– задана функція, 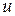– шуканий розв’язок. Виберемо в області 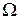скін­чен­ну множину точок 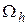, яка називається сіткою, а самі точки – вуз­лами. Тоді розв’язання крайової задачі (1) методом скінченних різниць (методом сіток) полягає в знаходженні таблиці значень 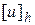функції 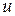в заданих вузлах сітки 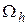. Саму таблицю значень 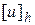прийнято називати сітковою функцією. Очевидно, що при згущенні сітки, тобто при 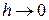, сіткова функція 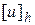буде давати більшу кількість інформації про точний розв’язок 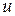крайової задачі (1), необ­хідну для встановлення 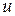. Більш детальний розгляд питання про відновлення функції за заданою таблицею її значень відноситься до компетенції теорії інтерполяції. Нас зараз цікавить задача обчислення сіткової функції 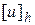, яку будемо інтерп­ретувати як точний розв’язок крайової задачі (1). Однак, на прак­ти­ці сіткову функцію 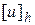отримати не можливо, тому шукають інші сіткові функції визначені на тій же сітці 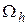, і які “збігаються” до 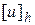при . 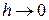Сіткова функція знаходиться як розв’язок від­по­від­ної різницевої задачі:

, (2)

де 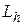- є різницевим аналогом вихідного диференціального оператора , а 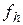– різницевий аналог правої частини 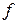. Різницева задача (2) представляє собою систему алгебраїчних рівнянь відносно функції , яку можна розглядати як вектор шуканих значень, розмірність якого співпадає з кількістю вузлів сітки 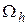. Рівняння (2) також часто на­зи­вають різницевою схемою задачі (1).

Існує декілька методів побудови різницевої схеми (2), найпрос­ті­шим і найбільш поширеним є метод розкладу в ряд Тейлора. Суть цього ме­тоду полягає в заміні похідних, які входять в диференціальний опе­ра­тор задачі (1), на так звані скінченні різниці. Не зменшуючи загаль­ності, розглянемо одновимірний випадок, тобто коли область 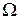– це відрізок і функція 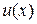визначена на цьому проміжку. Розкладемо функцію 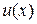в ряд Тейлора в околі точки :

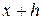(3)

Звідси будемо мати:

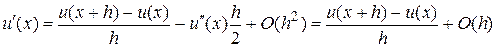
звідки випливає, що

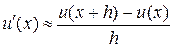(4)

Скінченно-різницеве співвідношення (4) для апроксимації першої похідної 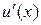називається правою скінченною різницею (вперед). Аналогічно можна отримати ліву скінченну різницю (назад):

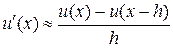(5)

скориставшись розкладом:

(6)

Віднявши (6) від (3) отримаємо апроксимацію

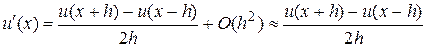(7)

центральною різницею . З співвідношень (3), (6), (7) видно, що права і ліва скінченні різниці мають перший порядок точності, а центральна різниця – другий порядок точності. Аналогічно можна отримати скінченно-різницеве співвідношення для апроксимації другої похідної. Додавши вирази (3) та (6), отримаємо:

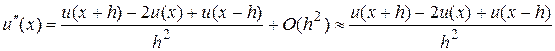(8)

де вираз в правій частині (8) називається центральною скінченною різ­ни­цею другого порядку. Аналогічно можна побудувати скінченну різ­­ницю другого порядку вперед (праву скінченну різницю)

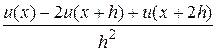(9)

та назад (ліву скінченну різницю):

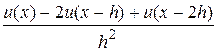. (10)

Сукупність вузлів сітки, які беруть участь в побудові скінченно-різницевої апроксимації похідної в деякій заданій точці 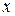, утворюють шаблон скінченної різниці. У наведених вище прикладах викорис­то­ву­ва­лися дво- та трьохточкові шаблони. Скінченно-різницеві співвід­но­шен­ня (4), (5), (7)-(10) мають місце і для апроксимації часткових п­о­хід­них. Скінченно-різницеву апроксимацію першої похідної можна уза­галь­нити у вигляді:

(11)

отримуючи тим самим ціле сімейство різницевих схем, залежних від деякого числового парметру 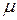. Зокрема, при маємо скінченну різ­ницю (4), при 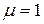- скінченну різницю (7), при 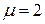- скінченну різницю (5).

Отже, основна ідея методу скінченних різниць полягає у заміні по­хід­них, що входять у задане диференціальне рівняння, на скінченні різниці. У результаті такої заміни неперервна операторна задача (1) зво­дить­ся до дискретної задачі (2) відносно вузлових значень шуканої функ­ції. Очевидно, що скінченні різниці дають лише наближене значен­ня похідних у вузлах сітки, або, як прийнято казати, апроксимують по­хід­­ні. Це означає, що внаслідок такої заміни виникає деяка похибка, яку називають похибкою апроксимації. Із співвідношень (3), (6), (8) видно, що похибка апроксимації залежить від величини кроку сітки . Цей факт залежності в теорії чисельних методів прийнято математично поз­на­чати 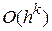. Такий запис означає, що апроксимація скінченною різ­ни­цею має 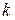-ий порядок точності, а також вказує, що величина похибки пря­мує до нуля при 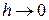. Сам показник степеня 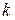характеризує швидкість прямування похибки до нуля, або, як прийнято казати, швид­кість збіжності. Це означає, що чим більше значення 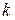, тим швидше по­хиб­ка прямуватиме до нуля (за одинакових інших умов).

Оскільки різницева схема (2) отримується шляхом апроксимації похідних скінченними різницями з певним порядком точності, то цілком логічно припустити, що тоді ця різницева схема буде в цілому апрок­си­му­вати вихідну диференціальну задачу (1). Це означає, що розв’язок різницевої задачі (2) буде апроксимувати точний розв’язок 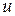задачі (1). В дійсності задача (2) представляє собою ціле сімейство різницевих схем залежних від , яке породжує послідовність наближених розв’язків , кожний з яких апроксимуватимите точний розв’язок 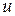з деякою по­хибкою. Виявляється, що величина цієї похибки та швидкість її пря­му­ван­ня до нуля (тобто швидкість збіжності послідовності наближених розв’язків до точного розв’язку) залежить від та порядку точнос­ті скінченної різниці. Залежність від означає, що величина похибки прямує до нуля при 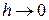, а порядок точності апроксимації скінченни­ми різницями визначає наскільки швидко це відбувається, тобто порядок швидкості збіжності. Слід зауважити, що якщо скінченна різниця має порядок точності , то це ще не означає, що різницева схема (2) авто­ма­тично має також 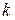-ий порядок точності. Дуже часто для досягнення цього доводиться застосовувати додаткові прийоми. Більше того, самого факту, що різницева схема (2) апроксимує задачу (1) дуже часто вияв­ляється замало для того, щоб гарантувати збіжність послідовності наб­ли­жених розв’язків до точного розв’язку 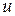задачі (1). Для цього пот­рібно, щоб різницева схема була ще й стійкою. Властивість стійкості є внутрішньою властивістю різницевої схеми, яка не залежить ні від ди­фе­рен­ціальної крайової задачі, ні від властивостей апроксимації та збіж­ності, її можна трактувати як рівномірну відносно чутливість роз­в’яз­ку різницевої схеми (2) до збурень правої частини 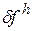. Отже, для того, щоб різницева схема (2) була збіжною, тобто послідовність наб­ли­жених роз­в’язків задач (2) збігалася до точного розв’язку 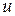задачі (1), во­на має бути апроксимуючою та стійкою. Наявність властивості збіж­ності є фундаментальною вимогою, яка накладається на різницеву схему (2) для чисельного розв’язання диференціальної крайової задачі (1). Як­що різницева схема є збіжною, то за її допомогою можна обчислити роз­в’я­зок задачі (1) з довільною наперед заданою точністю, вибираючи крок достатньо малим.

Для пояснення вище наведених теоретичних викладок розглянемо наступну задачу Коші

. (3)

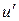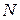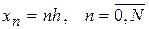Апроксимуємо першу похідну скінченною різницею вперед, для чого розіб’ємо відрізок [0;1] на рівних частин з кроком . Мно­жина точок утворює сітку 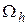. Позначимо 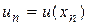. Тоді різницева схема задачі (3) буде мати вигляд:

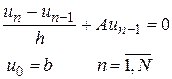(4)

З (4) можна отримати:

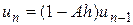, (5)

або з врахуванням початкової умови

. (6)

Точний розв’язок задачі (3) має вигляд:

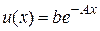. (7)

Знайдемо оцінку величини похибки наближеного розв’язку (6), яку в точці можна записати так:

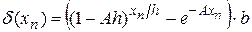. (8)

Знайти оцінку величини похібки означає дослідити, як веде себе 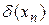при збільшенні кількості вузлів сітки, або при зменшенні кроку сітки . Для цього потрібно певним чином перетворити 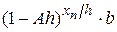. Після нескладних перетворень отримаємо:

Тоді

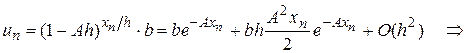
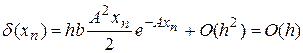. (9)

Співвідношення (9) означає, що похибка 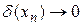при 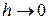, а величина похибки має перший порядок кроку . На цій підставі кажуть, що різницева схема має перший порядок точності. Якщо апроксимувати похідну 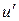центральною скінченною різницею першого порядку, то от­ри­маємо наступну різницеву схему:

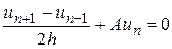. (10)

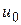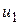Різницева схема (10) має другий порядок, тому необхідно задати дві початкові умови на і . Можна показати, що розв’язок різницевої схе­ми (10) збігатиметься до точного розв’язку, якщо покласти 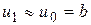. Нехай

.

Задамо початкове значення 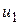з похибкою порядку , тобто: . Тоді можна показати, що:

, (11)

тобто, якщо початкове значення 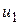задається з точністю до величини по­ряд­ку , то і величина похибки 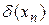буде порядку , тобто різни­це­ва схема (10) має другий порядок точності. Виявляється, що підвищення порядку точності задання початкового значення 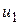, не впливає на підвищення порядку точності кінцевого результату.

Якщо задати перший порядок точності початкового значення 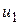, тобто покласти 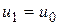, то можна показати, що в цьому випадку різ­ни­цева схема (10) буде мати також перший порядок точності. Тому прий­нято казати, що різницева схема (10) може дати більшу швидкість збіж­нос­ті, а саме швидкість збіжності з залишковим членом порядку , на від­міну від різницевої схеми (4), яка дає швидкість збіжності порядку . При чому, для того щоб отримати другий порядок точності в схемі (10), потрібно задати початкове значення 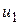, яке відрізняється від точного розв’язку в точці на величину порядку .

На рис.1 зображено документ MATHCAD, який містить програму розв’язання задачі Коші (3) за допомогою різницевих схем (4) та (10) з порівнянням отриманих наближених розв’язків з точним. З рис.1 видно, що різницева схема (10) з початковим значенням 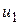із похибкою поряд­ку , яка має другий порядок точності, дає точніший результат ніж різницева схема (4), яка має перший порядок точності, на тій самій сітці. Для досягнення такої точності за допомогою різницевої схеми (4) потрібно брати більшу кількість вузлів (згустити сітку). Це й означає, що різницева схема (10) має більшу швидкість збіжності, а саме швидкість збіжності з залишковим членом порядку . Слід також зау­ва­жити, що для більшості практичних задач не вдається в явному виг­ляді виразити невідомі вузлові значення розв’язку через відомі, так як це зроблено у нашому прикладі за допомогою формули (6). У таких випад­ках різницева схема задається у вигляді системи лінійних алгебраїчних рівнянь відносно вектора вузлових значень шуканої функції.

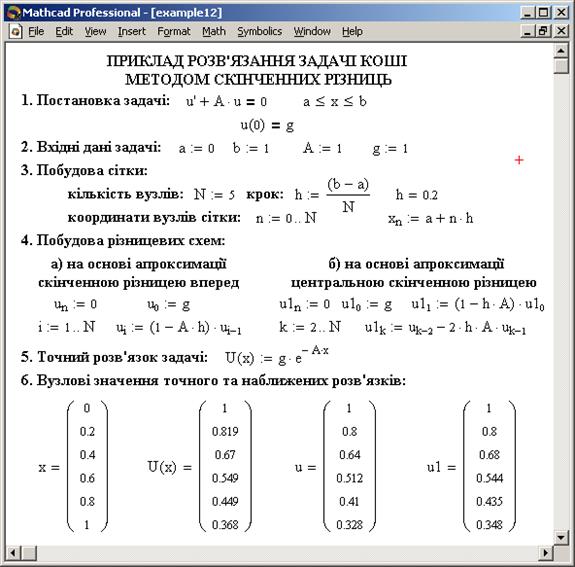
Рис.1. Приклад розв’язання задачі Коші для звичайного диферен­ціаль­ного рівняння за допомогою методу скінченних різниць