Пример расчёта лестничной площадки марки ЛПФ 28.13-5 по серии 1.252.1-4
Исходные данные
По степени ответственности здание относится ко второму классу (коэффициент надежности по назначению конструкции 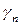 =0,95), по условиям эксплуатации ХC1.
=0,95), по условиям эксплуатации ХC1.
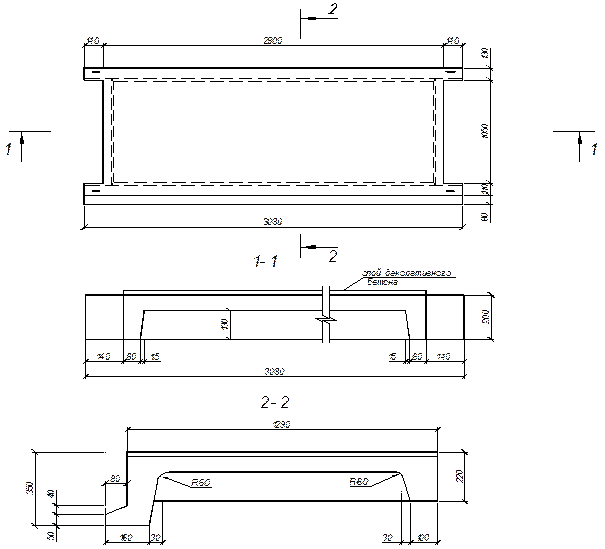
Рисунок 4.1- Конструкция лестничной площадки
Лестничная площадка изготавливается из бетона класса С20/25.
Расчётное сопротивление бетона сжатию: 
где  = 1,5 – частный коэффициент безопасности для бетона.
= 1,5 – частный коэффициент безопасности для бетона.
Расчётное сопротивление бетона растяжению:
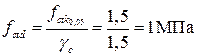 .
.
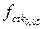 =1,5МПа (таблица 6.1 [3]).
=1,5МПа (таблица 6.1 [3]).
Арматурная сетка плиты лестничной площадки из проволочной арматуры класса S500 (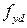 = 417 МПа – таблица 6.5[7]). Рабочая арматура продольных рёбер из стержневой арматуры класса S400 (
= 417 МПа – таблица 6.5[7]). Рабочая арматура продольных рёбер из стержневой арматуры класса S400 (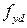 = 367 МПа – таблица 6.5[7]). Поперечная арматура – S240 (
= 367 МПа – таблица 6.5[7]). Поперечная арматура – S240 (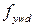 = 174 МПа – таблица 6.5[7]). Конструкция лестничной площадки показана на рисунке 4.1
= 174 МПа – таблица 6.5[7]). Конструкция лестничной площадки показана на рисунке 4.1
Расчёт плиты
Полку плиты при отсутствии поперечных рёбер рассчитывают как балочный элемент с защемлением на опорах (рисунок 4.2.). Расчётный пролёт равен расстоянию между продольными ребрами.
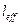 =
= 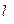 -130-110=1290-130-110=1050мм=1,050м.
-130-110=1290-130-110=1050мм=1,050м.
Подсчёт нагрузок приведён в таблице 4.1.
Таблица 4.1 – Нагрузки на 1 м2 плиты
кН/м2
| Вид нагрузки | Нормативная нагрузка | Частный
коэффициент безопасности
по нагрузке,
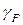
| Расчётная нагрузка |
1. Постоянная
1.1 Собственный вес плиты с отделочным слоем
0,09 м · 25 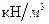 2. Переменная
2. Переменная
| 2,25 3,0 | 1,35 1,5 | 3,04 4,5 |
| Полная | 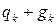 =5,25 =5,25
| 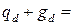 7,45 7,45
|
Расчётная схема плиты показана на рисунке 4.2.
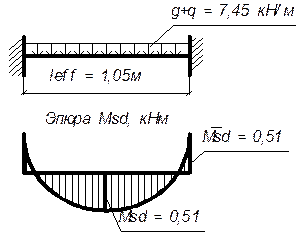
Рисунок 4.2 - Расчётная схема и эпюра Мsd плиты
Изгибающие моменты в пролёте и на опорах определяем по формуле 4.1:
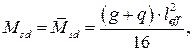 (4.1)
(4.1)
где 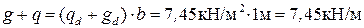
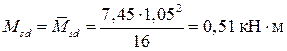 .
.
Рабочая высота сечения:
d = h – c (4.2)
где h = 90 – 20 = 70 мм – толщина плиты без отделочного слоя.
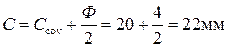
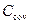 – защитный слой бетона плиты, принятый по таблице 11.4 [4] равным 20 мм.
– защитный слой бетона плиты, принятый по таблице 11.4 [4] равным 20 мм.
Ø – предполагаемый диаметр арматуры плиты.
d = 70 – 22 = 48 мм
Определим величину коэффициента 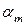 :
:
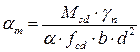 (4.3)
(4.3)
где α – коэффициент, учитывающий длительное действие нагрузки, неблагоприятный способ её приложения и принимаемый для тяжёлого бетона класса по прочности на сжатие не более С50/60 равным 1,0.
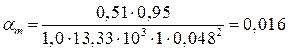
Определим граничную величину коэффициента:
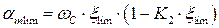 (4.4) где
(4.4) где 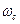 = 0,810; k = 0.416 – коэффициенты для определения параметров сжатой зоны бетона, определяется по таблице 6.5 [19].
= 0,810; k = 0.416 – коэффициенты для определения параметров сжатой зоны бетона, определяется по таблице 6.5 [19].
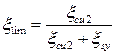 (4.5)
(4.5)
где 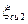 – относительные деформации, соответствующие предельной сжимаемости бетона.
– относительные деформации, соответствующие предельной сжимаемости бетона.
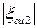 =3,5
=3,5 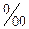 (таблица 6.1[3]).
(таблица 6.1[3]).
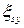 – относительная деформация арматуры, соответствующая пределу текучести арматурной стали:
– относительная деформация арматуры, соответствующая пределу текучести арматурной стали:
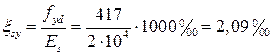 ,
,
тогда 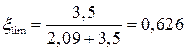
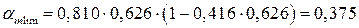 ;
;
Поскольку выполняется условие 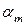 = 0,016<
= 0,016< 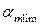 = 0,375, растянутая арматура достигла предельных деформаций, тогда
= 0,375, растянутая арматура достигла предельных деформаций, тогда
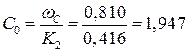
Находим значение  по формуле 7.6:
по формуле 7.6:
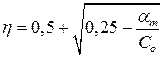 (4.6)
(4.6)
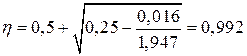 .
.
Величину требуемой площади растянутой арматуры определяем по формуле 4.7:
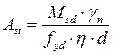 (4.7)
(4.7)
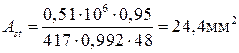
По таблице сортамента арматуры принимаем шесть стержней диаметром 4 мм S500 на 1 м плиты, для которых  = 75,4
= 75,4  >
> 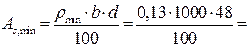
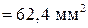 , где
, где 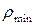 определено по таблице 11.1[6]:
определено по таблице 11.1[6]: 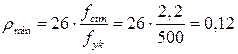 < 0,13. Принимаем
< 0,13. Принимаем 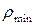 =0,13.
=0,13.
Принимаем сетку С-1 из арматуры диаметром 4 мм класса S500 с шагом рабочих стержней 150мм (распределительных с шагом 200м) с отгибом на опорах.
Расчёт лобового ребра
Расчётный пролёт ребра 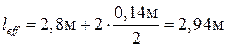 .
.
Расчётное сечение лобового ребра показано на рисунке 7.3.
Высота расчётного сечения h = 350 – 20 = 330 мм, ширина растянутой полки 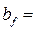 160мм; толщина растянутой полки
160мм; толщина растянутой полки 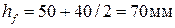 ; толщина сжатой полки
; толщина сжатой полки 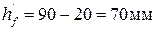 ; ширина ребра
; ширина ребра 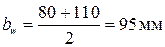 .
.
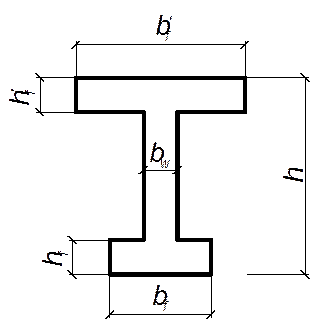
Рисунок 4.3- Расчётное сечение лобового ребра
При 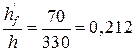 >0,1 в соответствии с указанием пункта 7.1.2.6. [3] за расчётную ширину сжатой полки принимаем из двух значений меньшее:
>0,1 в соответствии с указанием пункта 7.1.2.6. [3] за расчётную ширину сжатой полки принимаем из двух значений меньшее:
1) 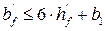
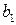 = 110 мм – ширина лобового ребра по верху,
= 110 мм – ширина лобового ребра по верху,
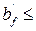 6·70+110 = 530 мм
6·70+110 = 530 мм
2) 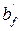
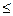
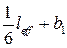
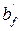
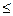
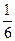 ·2940 + 110 = 600 мм
·2940 + 110 = 600 мм
Принимаем 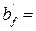 530 мм.
530 мм.
Подсчёт нагрузки на 1 м ребра приведён в таблице 4.2.
Таблица 4.2 – Нагрузки на 1м длины лобового ребра
в кН/м2
| Вид нагрузки | Нормативная нагрузка | Частный
коэффициент безопасности по нагрузке,
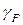
| Расчётная нагрузка |
1. Постоянная
1.1 Собственный вес ребра без учёта свесов (0,26·0,095+0,08·0,07)·25 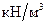 1.2 Собственный вес маршей
1.2 Собственный вес маршей
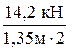 2. Переменная нагрузка на маршах
2. Переменная нагрузка на маршах
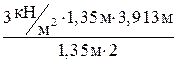
| 0,76 5,26 5,87 | 1,35 1,35 1,5 | 1,03 7,10 8,81 |
| Итого | 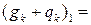 =11,89
=11,89
| 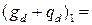 =16,97
=16,97
| |
3.Вес плиты с отделочным слоем
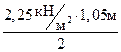 4.Переменная нагрузка на площадку
4.Переменная нагрузка на площадку
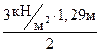
| 1,18 1,94 | 1,35 1,5 | 1,59 2,91 |
| Итого | 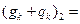 3,12 3,12
| 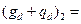 4,5 4,5
|
Расчетная схема ребра показана на рисунке 4.4:
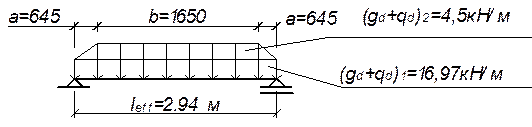
Рисунок 4.4 - Расчётная схема лобового ребра
 ,
,  .
.
Усилия от полной расчётной нагрузки:
- изгибающий момент
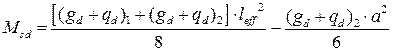 (4.8)
(4.8)
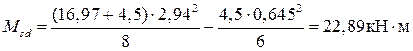
- поперечная сила
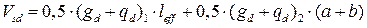 (4.9)
(4.9)
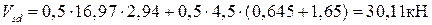 .
.
Расчёт рабочей арматуры лобового ребра
Для сечения с одиночным армированием поверяем условие, определяющее положение нейтральной оси. Предполагаем, что нейтральная ось проходит по нижней грани полки, и определяем область деформирования для прямоугольного сечения с шириной 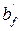 .
.
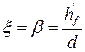 (4.10)
(4.10)
где d = h – c,
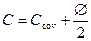 , (4.11)
, (4.11)
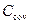 = 20мм (для условия эксплуатации ХC1 минимальное значение защитного слоя бетона
= 20мм (для условия эксплуатации ХC1 минимальное значение защитного слоя бетона 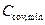 = 20 мм – таблица 11.4 [4]),
= 20 мм – таблица 11.4 [4]),
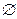 = 20
= 20 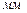 – предполагаемый максимальный диаметр арматуры,
– предполагаемый максимальный диаметр арматуры,
d = 330 – 30 = 300 мм
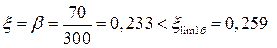 ,что указывает на то, что сечение находится в области деформирования 1б.
,что указывает на то, что сечение находится в области деформирования 1б.
По формулам таблицы 6.6 [19] находим величину изгибающего момента, воспринимаемого бетоном, расположенным в пределах высоты полки:
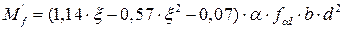 (4.12)
(4.12)
 Поскольку выполняется условие
Поскольку выполняется условие 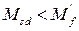 , то нейтральная ось располагается в пределах полки, в связи с этим дальнейший расчёт производим как для прямоугольного сечения имеющего размеры
, то нейтральная ось располагается в пределах полки, в связи с этим дальнейший расчёт производим как для прямоугольного сечения имеющего размеры 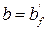 = 530 мм, d = 300 мм.
= 530 мм, d = 300 мм.
Определяем коэффициент 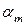 по формуле 4.3
по формуле 4.3
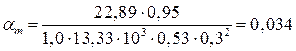
По таблице 6.7 [19] при 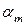 =0,034 определили, что сечение находится в области 1а и η = 0,970.
=0,034 определили, что сечение находится в области 1а и η = 0,970.
Находим величину требуемой площади растянутой арматуры по формуле 4.7:
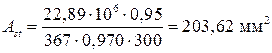 .
.
По таблице сортамента арматуры принимаем два стержня диаметром 12мм класса S400, для которых 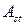 = 226
= 226  >
> 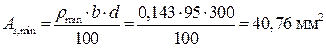 , где
, где 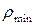 определено по таблице 11.1[6]:
определено по таблице 11.1[6]: 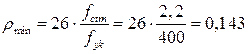 >0,13. Принимаем
>0,13. Принимаем 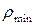 =0,143.
=0,143.
4.3.2 Расчет наклонного сечения лобового ребра на действие поперечной силы 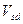
Поперечная сила от полной расчетной нагрузки 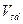 = 30,11 кН, с учётом коэффициента
= 30,11 кН, с учётом коэффициента 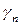 =0,95:
=0,95:
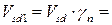 30,11·0,95 = 28,60 кН.
30,11·0,95 = 28,60 кН.
Расчёт производится на основе расчётной модели наклонных сечений.
Проверяем прочность лобового ребра по наклонной полосе между наклонными трещинами в соответствии с условием 4.13:
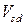
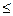
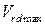 (4.13)
(4.13)
где 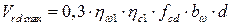 (4.14)
(4.14)
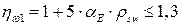 (4.15)
(4.15)
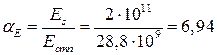 ,
,
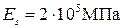 – модуль упругости арматуры.
– модуль упругости арматуры.
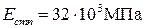 - модуль упругости для бетона С20/25, марки П1, П2 по удобоукладываемости естественного твердения.
- модуль упругости для бетона С20/25, марки П1, П2 по удобоукладываемости естественного твердения.
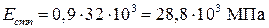 – для бетона подвергнутого тепловой обработке.
– для бетона подвергнутого тепловой обработке.
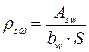 (4.16)
(4.16)
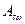 = 57
= 57 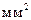 – площадь сечения двух поперечных стержней диаметром 6мм класса S240.
– площадь сечения двух поперечных стержней диаметром 6мм класса S240.
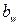 =95 мм – ширина ребра расчётного сечения.
=95 мм – ширина ребра расчётного сечения.
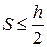 ,
, 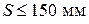 - шаг поперечных стержней каркасов Кр-1 лобового ребра.
- шаг поперечных стержней каркасов Кр-1 лобового ребра.
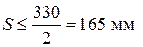 , принимаем S = 150 мм.
, принимаем S = 150 мм.
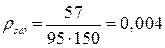 >
> 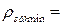
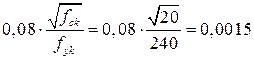 ;
; 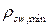 определено по пункту 11.2.5 [6];
определено по пункту 11.2.5 [6];
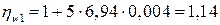 <1,3
<1,3
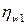 - коэффициент, определяемый по формуле 4.17:
- коэффициент, определяемый по формуле 4.17:
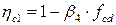 (4.17)
(4.17)
где 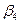 - коэффициент, принимаемый равным для тяжёлого бетона 0,01.
- коэффициент, принимаемый равным для тяжёлого бетона 0,01.
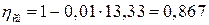 ;
;
Уточняем значение d:
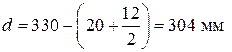 ;
; 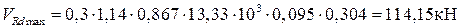
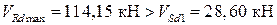
Следовательно, прочность по наклонной полосе между наклонными трещинами обеспечена.
По формуле 4.18 определим поперечную силу воспринимаемую бетоном и поперечной арматурой:
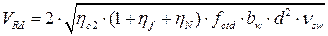 (4.18)
(4.18)
где 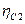 - коэффициент, принимаемый для тяжёлого бетона равным 2,0, учитывает влияние вида бетона.
- коэффициент, принимаемый для тяжёлого бетона равным 2,0, учитывает влияние вида бетона.
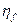 - коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах и определяемый по формуле 4.19:
- коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах и определяемый по формуле 4.19:
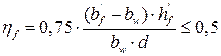 (4.19)
(4.19)
При этом 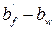
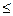
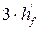
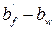 = 530 – 95 = 435 мм >
= 530 – 95 = 435 мм > 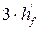 = 3·70 = 210 мм
= 3·70 = 210 мм
Для расчёта 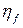 принимаем
принимаем 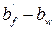 = 210 мм;
= 210 мм; 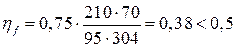 .
.
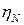 - коэффициент, учитывающий влияние продольных сил, при отсутствии продольных сил
- коэффициент, учитывающий влияние продольных сил, при отсутствии продольных сил 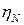 = 0.
= 0.
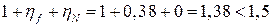
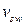 - усилие в поперечных стержнях на единицу длинны элемента определяемый по формуле 4.20
- усилие в поперечных стержнях на единицу длинны элемента определяемый по формуле 4.20
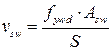 (4.20)
(4.20)
где 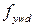 = 174 МПа – расчётное сопротивление поперечной арматуры (таблица 6.5 [7]).
= 174 МПа – расчётное сопротивление поперечной арматуры (таблица 6.5 [7]).
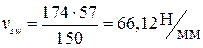 ;
;
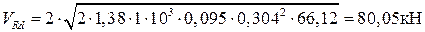 ;
;
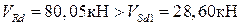 .
.
Следовательно, прочность на действие поперечной силы по наклонной трещине обеспечена.






