Апроксимуючу функцію нелінійних залежностей обирають з функцій визначеного типу, наприклад, з  ,
,  ,
, 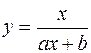 ,
, 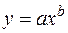 ,
,  ,
,  . Параметри
. Параметри  і
і  визначають за методом найменших квадратів, тому від нелінійних функціональних залежностей необхідно перейти до лінійних.
визначають за методом найменших квадратів, тому від нелінійних функціональних залежностей необхідно перейти до лінійних.
Нехай у системі координат 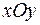 існує нелінійна залежність
існує нелінійна залежність  , неперервна і монотонна на відрізку
, неперервна і монотонна на відрізку 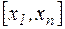 . Введемо зміні
. Введемо зміні 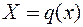 і
і 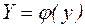 так, щоб у новій системі координат
так, щоб у новій системі координат 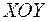 нелінійна залежність стала лінійною моделлю
нелінійна залежність стала лінійною моделлю  . Тоді точки з координатами
. Тоді точки з координатами 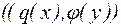 в площині
в площині 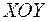 лежатимуть на прямій. Якщо серед значень
лежатимуть на прямій. Якщо серед значень  і
і 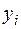 є від’ємні значення, чи значення, які дорівнюють нулю, то виконують нормування вихідних даних, тобто підбирають такі додатні значення
є від’ємні значення, чи значення, які дорівнюють нулю, то виконують нормування вихідних даних, тобто підбирають такі додатні значення 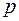 і
і 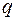 , що
, що 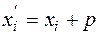 ,
, 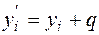 .
.
Покажемо, як від нелінійних функціональних залежностей перейти до лінійної моделі  .
.
Гіперболічна функціональна залежність 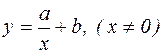 .
.
Покладемо 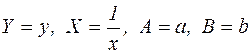 , одержимо
, одержимо  . За формулами переходу знайдемо параметри
. За формулами переходу знайдемо параметри  і
і  гіперболічної функціональної залежності
гіперболічної функціональної залежності 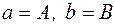 .
.
Дробово-лінійна функціональна залежність 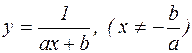 .
.
Знайдемо для даної функції обернену функцію 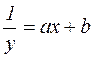 . Покладемо
. Покладемо 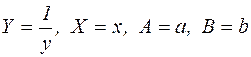 , одержимо
, одержимо  . За формулами переходу знайдемо параметри
. За формулами переходу знайдемо параметри  і
і  дробово-лінійної функціональної залежності
дробово-лінійної функціональної залежності 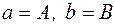 .
.
Дробово-раціональна функціональна залежність 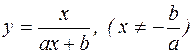 .
.
Знайдемо для даної функції обернену функцію 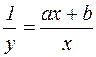 . Виконаємо алгебраїчні перетворення для правої частини рівності
. Виконаємо алгебраїчні перетворення для правої частини рівності 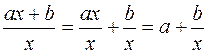 , отже,
, отже, 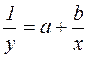 . Введемо нові зміні
. Введемо нові зміні 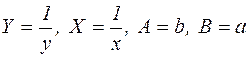 , одержимо лінійну модель
, одержимо лінійну модель  . За формулами переходу знайдемо параметри
. За формулами переходу знайдемо параметри  і
і  дробово-раціональної функціональної залежності
дробово-раціональної функціональної залежності 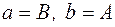 .
.
Ступенева функціональна залежність 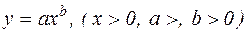 .
.
Логарифмуючи обидві частини рівності 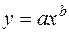 , знаходимо
, знаходимо 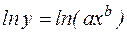 . Користуючись властивостями добутку і ступеня логарифмів, одержимо
. Користуючись властивостями добутку і ступеня логарифмів, одержимо 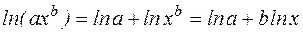 , отже,
, отже, 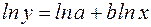 . Покладемо
. Покладемо 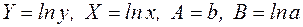 , одержимо лінійну модель
, одержимо лінійну модель  . За формулами переходу параметри
. За формулами переходу параметри  і
і  ступеневої функціональної залежності дорівнюють:
ступеневої функціональної залежності дорівнюють: 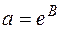 ,
, 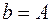 .
.
Експоненціальна функціональна залежність  .
.
Логарифмуючи обидві частини рівності  , знаходимо
, знаходимо 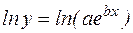 . За властивостями добутку і ступеня логарифмів, одержимо
. За властивостями добутку і ступеня логарифмів, одержимо 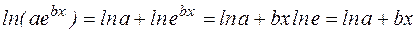 , отже,
, отже,  . Покладемо
. Покладемо 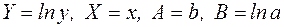 , одержимо
, одержимо  . За формулами переходу параметри
. За формулами переходу параметри  і
і  експоненціальної функціональної залежності дорівнюють:
експоненціальної функціональної залежності дорівнюють: 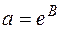 ,
, 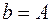 .
.
Логарифмічна функціональна залежність 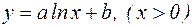 .
.
Щоб перейти від логарифмічної залежності до лінійної, зробимо підстановку 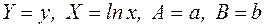 , одержимо лінійну модель
, одержимо лінійну модель  . За формулами переходу параметри
. За формулами переходу параметри  і
і  логарифмічної функціональної залежності дорівнюють:
логарифмічної функціональної залежності дорівнюють: 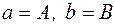 .
.
Способи вирівнювання нелінійних функціональних залежностей 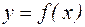 лінійною моделлю
лінійною моделлю  подано в таблиці 2.1.
подано в таблиці 2.1.
Таблиця 2.1 – Формули вирівнювання лінійною моделлю  нелінійних функціональних залежностей
нелінійних функціональних залежностей
| Емпірична формула | Спосіб вирівнювання |
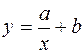
| 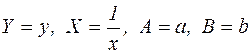
|
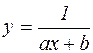
| 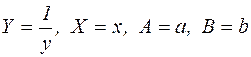
|
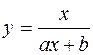
| 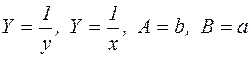
|
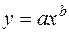
| 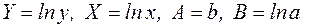
|

| 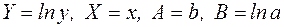
|
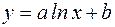
| 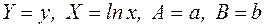
|
ПРАКТИЧНА ЧАСТИНА
Контрольний приклад
За даними лабораторних досліджень електричний струм (mkA), якій протікає по рослині протягом доби, залежить від експозиції взаємодії (год), про що свідчать наведені дані.
Таблиця 3.1 – Залежність електричного струму від експозиції взаємодії, 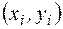
| Напруга, прикладена до рослини, U=60 B | |||
Взаємодія
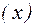 , год , год
| Електричний струм 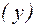 , mkA , mkA
| Взаємодія
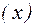 , год , год
| Електричний струм 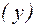 , mkA , mkA
|
| 2 | 232,8 | 14 | 289,8 |
| 4 | 236,1 | 16 | 302,3 |
| 6 | 238,4 | 18 | 320,4 |
| 8 | 251,3 | 20 | 351,6 |
| 10 | 268,4 | 22 | 378,8 |
| 12 | 276,5 | 24 | 410,3 |
Визначити апроксимуючу функцію з функцій визначеного типу  ,
,  ,
, 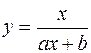 ,
, 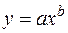 ,
,  ,
,  , яка описує залежність електричного струму від експозиції взаємодіїі побудувати її графік.
, яка описує залежність електричного струму від експозиції взаємодіїі побудувати її графік.
Розв’язання.
Побудуємо формули нелінійних функціональних залежностей за алгоритмом побудови апроксимуючої функціональної залежності. Знайдемо суми квадратів відхилень  вихідних значень
вихідних значень 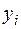 і значень апроксимуючих функцій
і значень апроксимуючих функцій  для кожної функціональної залежності, що розглядається.
для кожної функціональної залежності, що розглядається.
Гіперболічна функціональна залежність 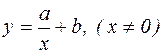 .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 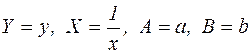 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 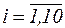 побудуємо таблицю даних
побудуємо таблицю даних 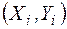 ,
, 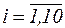 у новій системі координат
у новій системі координат 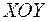 .
.
Таблиця 3.2 – Залежність електричного струму від експозиції взаємодії. Гіперболічна функціональна залежність

| 0,500 | 0,250 | 0,167 | 0,125 | 0,100 | 0,083 | 0,071 | 0,063 | 0,058 | 0,050 | 0,045 | 0,042 |

| 232,8 | 236,1 | 238,4 | 251,3 | 268,4 | 276,5 | 289,8 | 302,3 | 320,4 | 351,6 | 378,8 | 410,3 |
За даними таблиці 3.2 побудуємо розрахункову таблицю.
Таблиця 3.3 – Розрахункова таблиця для гіперболічної залежності
| № | 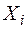
| 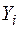
| 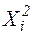
| 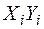
| 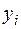 
| 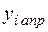
| 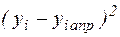
|
| 1 | 0,500 | 232,8 | 0,250 | 116,400 | 232,8 | 191,10 | 1738,83 |
| 2 | 0,250 | 236,1 | 0,063 | 59,025 | 236,1 | 262,11 | 676,47 |
| 3 | 0,167 | 238,4 | 0,028 | 39,733 | 238,4 | 285,78 | 2244,72 |
| 4 | 0,125 | 251,3 | 0,016 | 31,413 | 251,3 | 297,61 | 2144,91 |
| 5 | 0,100 | 268,4 | 0,010 | 26,840 | 268,4 | 304,71 | 1318,70 |
| 6 | 0,083 | 276,5 | 0,007 | 23,042 | 276,5 | 309,45 | 1085,56 |
| 7 | 0,071 | 289,8 | 0,005 | 20,700 | 289,8 | 312,83 | 530,34 |
| 8 | 0,063 | 302,3 | 0,004 | 18,894 | 302,3 | 315,37 | 170,70 |
| 9 | 0,056 | 320,4 | 0,003 | 17,800 | 320,4 | 317,34 | 9,38 |
| 10 | 0,050 | 351,6 | 0,003 | 17,580 | 351,6 | 318,92 | 1068,27 |
| 11 | 0,045 | 378,8 | 0,002 | 17,218 | 378,8 | 320,21 | 3433,18 |
| 12 | 0,042 | 410,3 | 0,002 | 17,096 | 410,3 | 321,28 | 7924,11 |
| Сума | 1,552 | 3556,7 | 0,391 | 405,740 | 3556,70 | 3556,70 | 22345,16 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
 ,
,  .
.
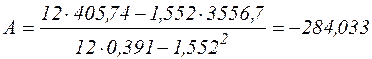 ,
,
 .
.
За формулами переходу знайдемо значення параметрів  і
і  гіперболічної функціональної залежності:
гіперболічної функціональної залежності: 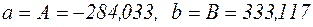 .
.
Отже, гіперболічна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 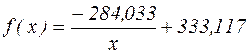 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 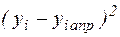 вихідних значень
вихідних значень 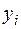 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.3.
. Результати обчислень занесемо в таблицю 3.3.
Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 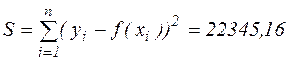 .
.
Дробово-лінійна функціональна залежність 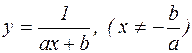 .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 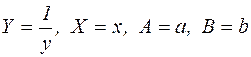 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 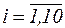 побудуємо нову таблицю
побудуємо нову таблицю 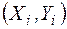 ,
, 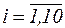 .
.
Таблиця 3.4 – Залежність електричного струму від експозиції взаємодії. Дробово-лінійна функціональна залежність

| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |

| 0,0043 | 0,0042 | 0,0042 | 0,0040 | 0,0037 | 0,0036 | 0,0035 | 0,0033 | 0,0031 | 0,0028 | 0,0026 | 0,0024 |
За даними таблиці 3.4 побудуємо розрахункову таблицю.
Таблиця 3.5 – Розрахункова таблиця для дробово-лінійної залежності
| № | 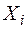
| 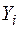
| 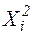
| 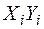
| 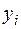 
| 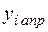
| 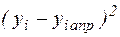
|
| 1 | 2 | 0,0043 | 4 | 0,0086 | 232,8 | 225,1 | 59,29 |
| 2 | 4 | 0,0042 | 16 | 0,0169 | 236,1 | 234,3 | 3,24 |
| 3 | 6 | 0,0042 | 36 | 0,0252 | 238,4 | 244,4 | 36 |
| Продовження таблиці | |||||||
| № | 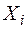
| 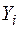
| 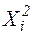
| 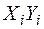
| 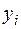 
| 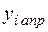
| 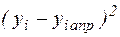
|
| 4 | 8 | 0,0040 | 64 | 0,0318 | 251,3 | 255,1 | 14,44 |
| 5 | 10 | 0,0037 | 100 | 0,0373 | 268,4 | 267,2 | 1,44 |
| 6 | 12 | 0,0036 | 144 | 0,0434 | 276,5 | 280,3 | 14,44 |
| 7 | 14 | 0,0035 | 196 | 0,0483 | 289,8 | 294,6 | 23,04 |
| 8 | 16 | 0,0033 | 256 | 0,0529 | 302,3 | 310,5 | 67,24 |
| 9 | 18 | 0,0031 | 324 | 0,0562 | 320,4 | 328,4 | 64 |
| 10 | 20 | 0,0028 | 400 | 0,0569 | 351,6 | 348,7 | 8,41 |
| 11 | 22 | 0,0026 | 484 | 0,0581 | 378,8 | 371,3 | 56,25 |
| 12 | 24 | 0,0024 | 576 | 0,0585 | 410,3 | 396,8 | 182,25 |
| Сума | 0,0418 | 0,4941 | 3556,7 | 3556,7 | 530,04 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
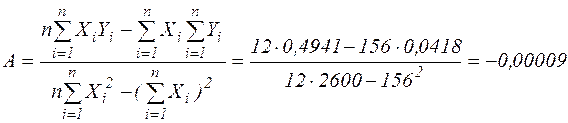 ,
,
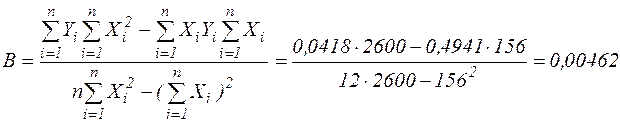 .
.
За формулами переходу знайдемо значення параметрів  і
і  гіперболічної функціональної залежності:
гіперболічної функціональної залежності: 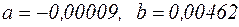 .
.
Дробово-лінійна функціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 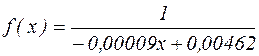 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 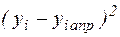 вихідних значень
вихідних значень 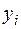 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.5.
. Результати обчислень занесемо в таблицю 3.5.
Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 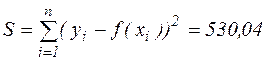 .
.
Дробово-раціональна функціональна залежність 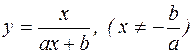 .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 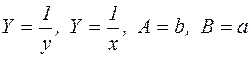 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 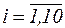 побудуємо нову таблицю
побудуємо нову таблицю 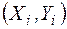 ,
, 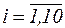 .
.
Таблиця 3.6 – Залежність електричного струму від експозиції взаємодії. Дробово-раціональна функціональна залежність

| 0,500 | 0,250 | 0,167 | 0,125 | 0,100 | 0,083 | 0,071 | 0,063 | 0,058 | 0,050 | 0,045 | 0,042 |

| 0,0043 | 0,0042 | 0,0042 | 0,0040 | 0,0037 | 0,0036 | 0,0035 | 0,0033 | 0,0031 | 0,0028 | 0,0026 | 0,0024 |
За даними таблиці 3.6 побудуємо розрахункову таблицю.
Таблиця 3.7 – Розрахункова таблиця для дробово-раціональної залежності
| № | 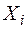
| 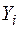
| 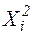
| 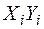
| 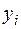 
| 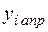
| 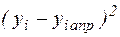
|
| 1 | 0,500 | 0,0043 | 0,250 | 0,0021 | 232,8 | 217,44 | 235,93 |
| 2 | 0,250 | 0,0042 | 0,063 | 0,0011 | 236,1 | 263,38 | 744,20 |
| 3 | 0,167 | 0,0042 | 0,028 | 0,0007 | 238,4 | 283,25 | 2011,52 |
| 4 | 0,125 | 0,0040 | 0,016 | 0,0005 | 251,3 | 294,34 | 1852,44 |
| 5 | 0,100 | 0,0037 | 0,010 | 0,0004 | 268,4 | 301,43 | 1090,98 |
| 6 | 0,083 | 0,0036 | 0,007 | 0,0003 | 276,5 | 306,32 | 889,23 |
| 7 | 0,071 | 0,0035 | 0,005 | 0,0002 | 289,8 | 309,86 | 402,40 |
| 8 | 0,063 | 0,0033 | 0,004 | 0,0002 | 302,3 | 312,58 | 105,68 |
| 9 | 0,056 | 0,0031 | 0,003 | 0,0002 | 320,4 | 314,79 | 31,47 |
| 10 | 0,050 | 0,0028 | 0,003 | 0,0001 | 351,6 | 316,58 | 1226,40 |
| № | 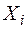
| 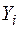
| 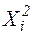
| 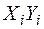
| 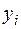 
| 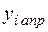
| 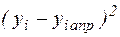
|
| 11 | 0,045 | 0,0026 | 0,002 | 0,0001 | 378,8 | 317,37 | 3773,64 |
| 12 | 0,042 | 0,0024 | 0,002 | 0,0001 | 410,3 | 319,36 | 8270,08 |
| Сума | 1,552 | 0,0418 | 0,391 | 0,0061 | 3556,7 | 3556,7 | 20633,99 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
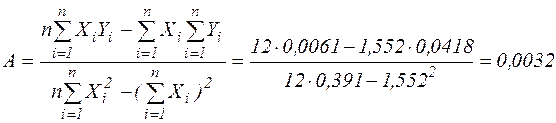 ,
,
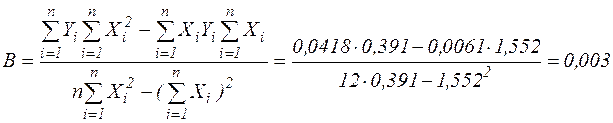 .
.
За формулами переходу знайдемо значення параметрів  і
і  дробово-раціональної функціональної залежності:
дробово-раціональної функціональної залежності: 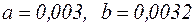 .
.
Отже, дробово-раціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 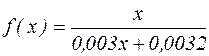 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 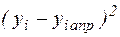 вихідних значень
вихідних значень 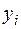 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.7.
. Результати обчислень занесемо в таблицю 3.7.
Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 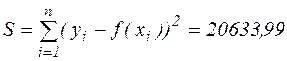 .
.
Ступенева функціональна залежність 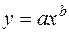 .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 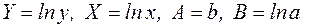 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 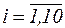 побудуємо нову таблицю
побудуємо нову таблицю 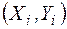 ,
, 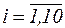 .
.
Таблиця 3.8 – Залежність електричного струму від експозиції взаємодії. Ступенева функціональна залежність

| 0,693 | 1,386 | 1,792 | 2,079 | 2,303 | 2,485 | 2,639 | 2,773 | 2,890 | 2,996 | 3,091 | 3,178 |

| 5,450 | 5,464 | 5,476 | 5,527 | 5,592 | 5,622 | 5,669 | 5,711 | 5,770 | 5,862 | 5,937 | 6,017 |
За даними таблиці 3.8 побудуємо розрахункову таблицю.
Таблиця 3.9 – Розрахункова таблиця для ступеневої залежності
| № | 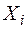
| 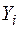
| 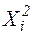
| 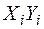
| 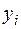 
| 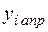
| 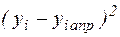
|
| 1 | 0,693 | 5,450 | 0,480 | 3,778 | 232,8 | 201,95 | 951,7225 |
| 2 | 1,386 | 5,464 | 1,922 | 7,575 | 236,1 | 235,66 | 0,1936 |
| 3 | 1,792 | 5,474 | 3,210 | 9,808 | 238,4 | 258,03 | 385,3369 |
| 4 | 2,079 | 5,527 | 4,324 | 11,492 | 251,3 | 275,11 | 566,9161 |
| 5 | 2,303 | 5,592 | 5,302 | 12,877 | 268,4 | 289,18 | 431,8084 |
| 6 | 2,485 | 5,622 | 6,175 | 13,971 | 276,5 | 301,17 | 608,6089 |
| 7 | 2,639 | 5,669 | 6,965 | 14,961 | 289,8 | 311,44 | 468,2896 |
| 8 | 2,773 | 5,711 | 7,687 | 15,835 | 302,3 | 321,08 | 352,6884 |
| 9 | 2,890 | 5,770 | 8,354 | 16,676 | 320,4 | 329,45 | 81,9025 |
| 10 | 2,996 | 5,862 | 8,974 | 17,562 | 351,6 | 337,46 | 199,9396 |
| 11 | 3,091 | 5,937 | 9,555 | 18,352 | 378,8 | 344,75 | 1159,403 |
| 12 | 3,178 | 6,017 | 10,100 | 19,122 | 410,3 | 351,42 | 3466,854 |
| Сума | 28,305 | 68,096 | 73,049 | 162,010 | 3556,7 | 3556,7 | 8673,663 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
 ,
,  .
.
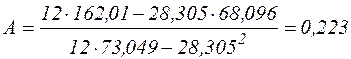 ,
,
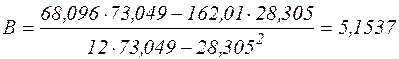 .
.
За формулами переходу параметри  і
і  ступеневої функціональної залежності дорівнюють:
ступеневої функціональної залежності дорівнюють: 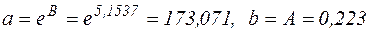 .
.
Отже, ступенева залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 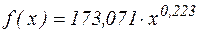 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 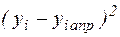 вихідних значень
вихідних значень 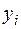 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.9. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції
. Результати обчислень занесемо в таблицю 3.9. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 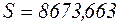 .
.
Експоненціальна функціональна залежність  .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 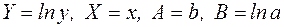 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 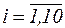 побудуємо нову таблицю
побудуємо нову таблицю 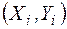 ,
, 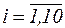 .
.
Таблиця 3.10 – Залежність електричного струму від експозиції взаємодії. Експоненціальна функціональна залежність

| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |

| 5,450 | 5,464 | 5,476 | 5,527 | 5,592 | 5,622 | 5,669 | 5,711 | 5,770 | 5,862 | 5,937 | 6,017 |
За даними таблиці 3.10 побудуємо розрахункову таблицю.
Таблиця 3.11 – Розрахункова таблиця для експоненціальної залежності
| № | 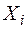
| 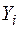
| 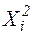
| 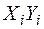
| 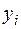 
| 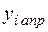
| 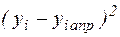
|
| 1 | 2 | 5,450 | 4 | 10,90 | 232,8 | 219,13 | 186,87 |
| 2 | 4 | 5,464 | 16 | 21,86 | 236,1 | 230,83 | 27,77 |
| 3 | 6 | 5,474 | 36 | 32,84 | 238,4 | 243,21 | 23,14 |
| 4 | 8 | 5,527 | 64 | 44,21 | 251,3 | 256,12 | 23,23 |
| 5 | 10 | 5,592 | 100 | 55,92 | 268,4 | 269,79 | 1,93 |
| 6 | 12 | 5,622 | 144 | 67,47 | 276,5 | 284,18 | 58,98 |
| 7 | 14 | 5,669 | 196 | 79,37 | 289,8 | 299,34 | 91,01 |
| 8 | 16 | 5,711 | 256 | 91,38 | 302,3 | 315,32 | 169,52 |
| 9 | 18 | 5,770 | 324 | 103,85 | 320,4 | 332,14 | 137,83 |
| 10 | 20 | 5,862 | 400 | 117,25 | 351,6 | 349,89 | 2,92 |
| 11 | 22 | 5,937 | 484 | 130,61 | 378,8 | 368,54 | 105,27 |
| 20 | 24 | 6,017 | 576 | 144,41 | 410,3 | 388,21 | 487,97 |
| Сума | 68,096 | 900,08 | 3556,7 | 3556,7 | 1316,44 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
 ,
,
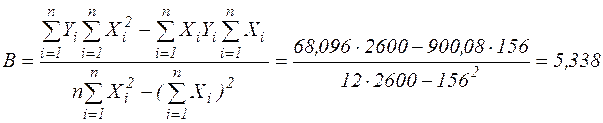 .
.
За формулами переходу параметри  і
і  експоненціальної функціональної залежності дорівнюють:
експоненціальної функціональної залежності дорівнюють: 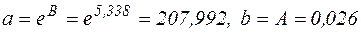 .
.
Отже, експоненціальна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 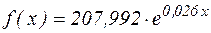 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 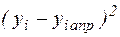 вихідних значень
вихідних значень 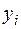 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.11. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції
. Результати обчислень занесемо в таблицю 3.11. Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 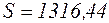 .
.
Логарифмічна функціональна залежність 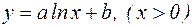 .
.
Побудуємо лінійну модель  , використавши відповідні формули переходу до нових координат
, використавши відповідні формули переходу до нових координат 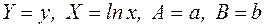 (таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії
(таблиця 2.1). За вихідною таблицею залежності електричного струму від експозиції взаємодії  ,
, 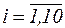 побудуємо нову таблицю
побудуємо нову таблицю 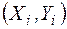 ,
, 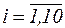 .
.
Таблиця 3.12 – Залежність електричного струму від експозиції взаємодії. Логарифмічна функціональна залежність

| 0,69 | 1,39 | 1,79 | 2,08 | 2,30 | 2,48 | 2,64 | 2,77 | 2,89 | 3,00 | 3,09 | 3,18 |

| 232,8 | 236,1 | 238,4 | 251,3 | 268,4 | 276,5 | 289,8 | 302,3 | 320,4 | 351,6 | 378,8 | 410,3 |
За даними таблиці 3.12 побудуємо розрахункову таблицю.
Таблиця 3.13 – Розрахункова таблиця для логарифмічної залежності
| № | 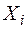
| 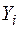
| 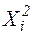
| 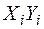
| 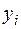 
| 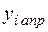
| 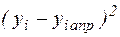
|
| 1 | 0,69 | 232,8 | 0,48 | 161,36 | 232,8 | 187,38 | 2062,86 |
| 2 | 1,39 | 236,1 | 1,92 | 327,30 | 236,1 | 232,75 | 11,25 |
| 3 | 1,79 | 238,4 | 3,21 | 427,16 | 238,4 | 259,28 | 436,11 |
| 4 | 2,08 | 251,3 | 4,32 | 522,56 | 251,3 | 278,11 | 718,86 |
| 5 | 2,30 | 268,4 | 5,30 | 618,01 | 268,4 | 292,72 | 591,26 |
| 6 | 2,48 | 276,5 | 6,17 | 687,08 | 276,5 | 304,65 | 792,34 |
| 7 | 2,64 | 289,8 | 6,96 | 764,80 | 289,8 | 314,74 | 621,87 |
| 8 | 2,77 | 302,3 | 7,69 | 838,15 | 302,3 | 323,48 | 448,45 |
| 9 | 2,89 | 320,4 | 8,35 | 926,08 | 320,4 | 331,19 | 116,32 |
| 10 | 3,00 | 351,6 | 8,97 | 1053,30 | 351,6 | 338,08 | 182,76 |
| 11 | 3,09 | 378,8 | 9,55 | 1170,89 | 378,8 | 344,32 | 1188,95 |
| 12 | 3,18 | 410,3 | 10,10 | 1303,96 | 410,3 | 350,01 | 3634,45 |
| Сума | 28,30 | 3556,7 | 73,05 | 8800,65 | 3556,7 | 3556,7 | 10805,48 |
Знайдемо значення параметрів  і
і  лінійної моделі
лінійної моделі  за формулами:
за формулами:
 ,
,  .
.
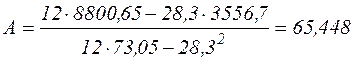 ,
,
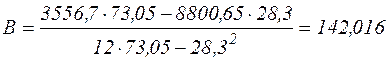 .
.
За формулами переходу параметри  і
і  логарифмічної функціональної залежності дорівнюють:
логарифмічної функціональної залежності дорівнюють: 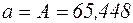 ,
, 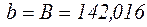 .
.
Логарифмічна функціональна залежність, яка описує залежність електричного струму від експозиції взаємодії, має вигляд 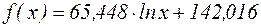 .
.
Знайдемо значення апроксимуючої функції для вихідних значень змінної  і квадрати відхилень
і квадрати відхилень 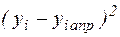 вихідних значень
вихідних значень 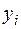 і значень апроксимуючої функції
і значень апроксимуючої функції  . Результати обчислень занесемо в таблицю 3.13.
. Результати обчислень занесемо в таблицю 3.13.
Сума квадратів відхилень вихідних значень і значень апроксимуючої функції 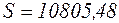 .
.
Оберемо апроксимуючу функцію за






