Векторы.
- скалярное произведение векторов
- скалярное произведение в координатной форме
- условие перпендикулярности век-ров
- условие параллельности (коллинеарности) векторов
- длина вектора
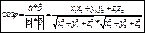- угол между век-рами
- векторное произведение век-ров
- смешанное произведение векторов
- формула вычисления смешанного произ-ния век-ров
Прямая на плоскости.
- уравнение прямой с угловым коэффициентом k
- уравнение прямой, проходящей через одну точку
- уравнение прямой, проходящей через 2 точки
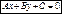- общее уравнение прямой
- уравнение прямой в отрезках
- угловой коэффициент
- условие параллельности
- условие перпендикулярности
- угол между прямыми
- расстояние от точки до прямой
Плоскость в пространстве.
- общее ур-ие плоскости
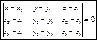- уравнение плоскости, проходящей через 3 точки
- уравнение плоскости в отрезках
- нормальное уравнение плоскости
- направляющие косинусы вектора
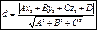- расстояние от точки до плоскости
- условие параллельности плоскостей
- условие перпендикулярности плоскостей
- угол между плос-ми
Прямая в пространстве.
- общее уравнение прямой
- каноническое уравнение прямой
- параметрическое уравнение прямой
- условие параллельности прямых
- условие перпендикулярности прямых
- угол между прямыми
Этапы перехода от общего уравнения прямой к каноническому:
1) Находится вектор 
.
2) Находится точка М0 (x0, y0, z0), любая из этих координат приравнивается к 0,
оставшиеся координаты находятся из системы уравнений общего уравнения прямой.
3) Составляется каноническое или параметрическое уравнение прямой.
Производные.
(u±v)’=u’±v’; (uv)’ = u’v + uv’; (u/v)’ = u’v - uv’/v2
(un)’=n*un-1*u’; yx’=yt’/xt’; F’=-Fx’/Fy’; (f(u(x)))’=f’(u(x))*u’(x)
| функция | произв-ая | функция | произв-ая |
| k | sin x | cos x | |
| kx | k | cos x | -sin x |
| xn | n*xn-1 | tg x | 1/ cos2 x |
| 1/x | -1/x2 | ctg x | -1/ sin2 x |
| 1/xn | -n/xn+1 | sin2 x | sin 2x |
| 1/2
| cos2 x | -sin 2x |
| 
| arcsin x | 
|
| logax | 1/x*ln a | arccos x | 
|
| ln x | 1/x | arctg x | 
|
| ex | ex | arcctg x | 
|
Таблица неопределенных интегралов
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
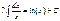
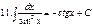
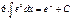
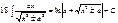
Подведение под знак дифференциала: 
 Дифференциальные уравнения с пост-ми коэффициентами
| |||
| № | корни k2+pk+q=0 | вид общего решения | |
| D>0, k1≠k2 | 
| ||
| D=0, k1=k2 |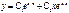 
| ||
| D<0, k1/2=α±βi | 
| ||
| № | f(x) | кратность корней | вид yчаст. |
| p*eαx (p-число) | α≠k1, α≠k2 | A*eαx | |
| α=k1, α≠k2 | A*x*eαx | ||
| α=k1, α=k2 | A*x2*eαx | ||
| Pn(x)*eαx (Pn(x)-выражение) | α≠k1, α≠k2 | (Anxn+An-1xn-1+…+A0)eαx | |
| α=k1, α≠k2 | (Anxn+…+A0)x*eαx | ||
| α=k1, α=k2 | (Anxn+…+A0)x2*eαx | ||
| Pn(x) | k1≠0, k2≠0 | Anxn+An-1xn-1+…+A0 | |
| k1=0 или k2=0 | (Anxn+…+A0)x | ||
| Mcosβx+Nsinβx | k1/2≠α±βi | Acosβx+Bsinβx | |
| k1/2=α±β | (Acosβx+Bsinβx)x |
Методы интегрирования:
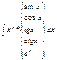I. Интегрирование по частям: 
1) u = xn
2) u = 
3) u = ex
II. Замена переменных: 
| Таблица первообразных | |||
| функция | первообразная | функция | первообразная |
| xn (n≠-1) | xn+1/n+1 | cos x | sin x |
| 1/ x | ln x | 1/sin2 x | -ctg x |
| 1/ xn | -1/(n-1)*xn-1 | 1/cos2 x | tg x |
1/ 
| 2*
| sin(kx+b) | -1/k*cos(kx+b) |
| k | kx | cos(kx+b) | 1/k*sin(kx+b) |
| ex | ex | (kx+b)n | (kx+b)n+1/k(n+1) |
| ax | ax/ln a | 1/kx+b | 1/k*ln(kx+b) |
| sin x | -cos x | ekx+b | 1/k* ekx+b |
Интегрирование тригонометрических функций
I. 
1) m - чёт.: cos x = t
n - нечёт.: sin2x = 1- cos2x
2) m - нечёт.: cos2x = 1- sin2x
n - чёт.: sin x = t
3) m - чёт.:
 |
n - чёт.:
4) m - нечёт.: cos2x = 1- sin2x
n - нечёт.: sin x = t
II.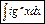 
; 
Обязательно отделяется tg2x или ctg2x:
III. 
Действует унив-ная триг-кая подстановка:
; 
; 
 |
x = 2arctg t;
IV. 
; 
;
sinα*cosβ=1/2(sin(α+β)-sin(α-β))
cosα*cosβ=1/2(cos(α-β)+cos (α+β))
sinα*sinβ=1/2(cos(α-β)-cos(α+β))
Пределы:
I. Неопределённость 
:
1) если степени чис-ля и зн-ля равны, то предел
равен отношению коэфицентов при степенях.
2) если степень чис-ля > зн-ля, то предел = ∞.
3) если степень зн-ля > чис-ля, то предел = 0.
II. Неопределённость 
:
Необходимо чис-ль и зн-ль разложить на
множ-ли, при этом должно присутствовать
выражение x-a (а-число, к которому стрем-ся х).
 |
1-ый замечательный предел:
 |
2-ой замечательный предел:
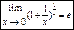
Достаточные признаки сходимости числовых рядов:
1) 1 признак сравнения: Пусть даны два ряда Un и Vn, причем эл-ты 1 не превосходят эл-тов 2, тогда:
Если ряд 2 сход-ся, то и ряд 1 сход-ся
Если ряд 1 расход-ся, то и ряд 2 расход-ся
2) 2 признак сравнения: Если для рядов Un и Vn сущ-ет предел 
, то ряды одновременно сход-ся или расход-ся
3) признак Даламбера: Если сущ-ет предел
то, если D>1- ряд расх-ся; D<1 - ряд сходится;
D=1 -?
4) радикальный признак Коши: Если сущ-ет предел
k>1 - ряд расх-ся; k<1 - ряд сход-ся; k=1 -?
5) интегральный признак Коши: Пусть дан ряд Un, в котором U1≥U2≥…≥Un…., тогда ряд сход-ся, если в рез-те решения данного интеграла получ-ся число и расх-ся, если получ-ся ∞.
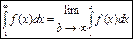
Основные виды сходящихся и расходящихся рядов:
1) геометрический ряд:
|q|<1- ряд сход-ся
|q|≥1- ряд расход-ся
2) гармонический ряд:
 |
- ряд расход-ся
3) обобщённый геометрический ряд:
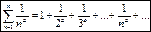α>1- ряд сход-ся
α≤1- ряд расход-ся
