МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Лабораторная работа
ИССЛЕДОВАНИЕ АПЕРИОДИЧЕСКОГО УСИЛИТЕЛЯ
НЕПРЕРЫВНЫХ СИГНАЛОВ
Утверждено
на заседании кафедры
_____________________
Москва, 2005 г.
Цель работы – теоретическое и экспериментальное исследование малосигнального транзисторного апериодического усилителя. Условие малости сигнала позволяет ограничиться изучением линейных искажений, возникающих при усилении.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ.
Апериодическими называются такие усилители, нагрузкой которых служат апериодические (нерезонансные) цепи. Такие усилители получили широкое распространение в различных областях современной радиоэлектроники. Они применяются и как усилители низкой частоты, и как широкополосные или импульсные усилители.
Для оценки свойств апериодических усилителей используются основные показатели: коэффициент усиления, амплитудно-частотная (АЧХ) и фазочастотная (ФЧХ) характеристики, полоса частот, переходная характеристика, динамический диапазон и амплитудная характеристика, входная и выходная проводимости и другие.
Свойства апериодических усилителей будем изучать на примере каскада, принципиальная схема которого изображена на рис.1.
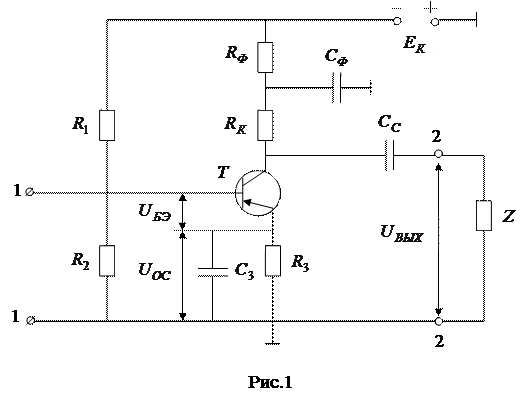 |
Нагрузкой транзистора Т по переменному току являются резистор 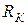 и включенная через разделительный конденсатор (ёмкость связи)
и включенная через разделительный конденсатор (ёмкость связи) 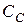 цепь потребителя (Z). Резисторы
цепь потребителя (Z). Резисторы 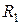 ,
, 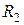 и
и 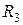 предназначены для задания режима транзистора по постоянному току и стабилизации этого режима по отношению к технологическому и температурному разбросу параметров транзистора.
предназначены для задания режима транзистора по постоянному току и стабилизации этого режима по отношению к технологическому и температурному разбросу параметров транзистора.
Стабилизация основана на действии отрицательной обратной связи по току. Для того, чтобы эта обратная связь не уменьшала усиление на переменном токе, резистор 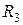 шунтируют конденсатором
шунтируют конденсатором 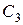 .
.
1.Расчёт параметров транзистора.
В качестве активного элемента в изучаемом апериодическом усилителе используется биполярный транзистор, включенный по схеме с общим эмиттером (ОЭ). Поэтому начнём с описания свойств транзистора ОЭ, определяющих работу апериодического усилителя.
Гибридная П-образная физическая эквивалентная схема транзистора ОЭ приведена на рис.2.
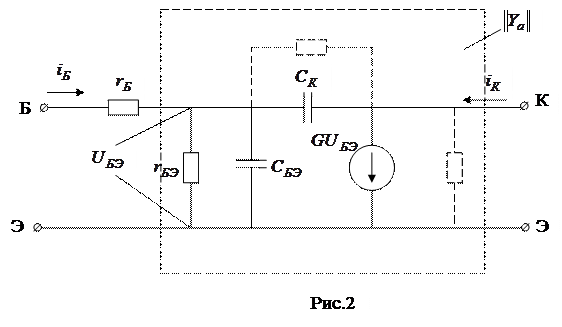
Точка «Б» разделяет «пассивную» и «активную» области транзистора. «Пассивная» область учитывает сопротивление тела базы (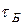 ). «Активная» - собственно эмиттерный переход (
). «Активная» - собственно эмиттерный переход (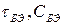 ), выходной управляемый генератор тока (
), выходной управляемый генератор тока (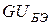 ) с проводимостью
) с проводимостью 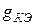 , а также элементы, представляющие коллекторный переход (
, а также элементы, представляющие коллекторный переход (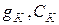 ). Крутизна выходного генератора тока G (действительная величина, имеющая размерность проводимости) связывает величину тока с напряжением на собственно эмиттерном переходе (
). Крутизна выходного генератора тока G (действительная величина, имеющая размерность проводимости) связывает величину тока с напряжением на собственно эмиттерном переходе (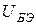 ).
).
Расчёт элементов эквивалентной схемы обычно основывается на справочных данных. Справочные данные представляют совокупность измеряемых параметров, которые контролируются в ходе изготовления транзисторов. Режим транзистора при измерениях (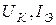 ) оговаривается (типовой режим). Наиболее просто расчёт осуществляется тогда, когда режим транзистора в усилителе близок к типовому. В этом случае достаточен следующий минимум справочных данных:
) оговаривается (типовой режим). Наиболее просто расчёт осуществляется тогда, когда режим транзистора в усилителе близок к типовому. В этом случае достаточен следующий минимум справочных данных:
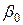 – низкочастотный коэффициент передачи тока в схеме ОЭ;
– низкочастотный коэффициент передачи тока в схеме ОЭ;
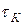 – постоянная времени коллекторной цепи;
– постоянная времени коллекторной цепи;
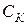 - ёмкость коллекторного перехода;
- ёмкость коллекторного перехода;
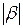 - модуль коэффициента передачи тока в схеме ОЭ;
- модуль коэффициента передачи тока в схеме ОЭ;
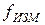 - частота, на которой измерена величина
- частота, на которой измерена величина 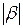 .
.
Элементы эквивалентной схемы определяются по формулам:
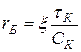 ;
; 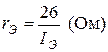 ;
; 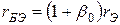 ; (1)
; (1)
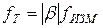 ;
; 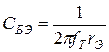 ;
; 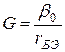 .
.
Для сплавных транзисторов 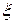 =1, а для сплавно-диффузионных
=1, а для сплавно-диффузионных 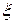 =2.
=2.
Ток покоя эмиттера 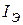 берется в мА (эта формула верна только для температуры 20° С).
берется в мА (эта формула верна только для температуры 20° С).
Частота 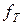 называется граничной частотой транзистора.
называется граничной частотой транзистора.
Рекомендуем учащимся самостоятельно провести расчёт сплавно- диффузионного транзистора П-416А, для которого в режиме 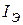 =5мА и
=5мА и 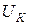 =5В справочные данные имеют следующие значения:
=5В справочные данные имеют следующие значения:
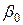 =60¸125;
=60¸125; 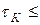 500псек;
500псек; 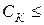 8пф;
8пф; 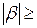 3;
3; 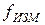 =20МГц.
=20МГц.
Проводимости 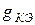 и
и 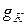 (пунктир на рис.2) невелики и их влиянием на работу усилителей часто можно пренебречь; промышленность, как правило, не информирует потребителей о величинах этих проводимостей. Поэтому в дальнейшем будем полагать
(пунктир на рис.2) невелики и их влиянием на работу усилителей часто можно пренебречь; промышленность, как правило, не информирует потребителей о величинах этих проводимостей. Поэтому в дальнейшем будем полагать 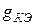 =0 и
=0 и 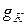 =0.
=0.
Последующее изложение основано на использовании Y -параметров эквивалентной схемы рис.2. Напомним кратко процедуру вычисления этих параметров. Эквивалентную схему рис.2 можно рассматривать как четырехполюсник с матрицей коэффициентов 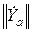 , представляющий «активную» область транзистора, во входную цепь которого последовательно включено сопротивление
, представляющий «активную» область транзистора, во входную цепь которого последовательно включено сопротивление 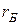 . Y – параметры в этом случае выражаются следующим образом:
. Y – параметры в этом случае выражаются следующим образом:
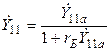 ;
; 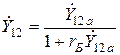 ;
; 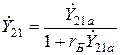 ;
;
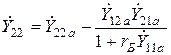 (2)
(2)
Определим выражение 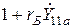 , входящее во все формулы, а поэтому имеющее первостепенное значение. Пользуясь входной проводимостью
, входящее во все формулы, а поэтому имеющее первостепенное значение. Пользуясь входной проводимостью 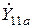 четырёхполюсника, представляющего «активную» область транзистора
четырёхполюсника, представляющего «активную» область транзистора
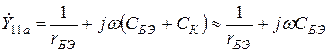 (3)
(3)
Находим
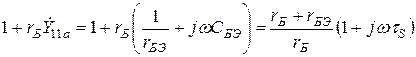 . (4)
. (4)
Здесь 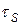 - постоянная времени, обратная граничной частоте транзистора по крутизне
- постоянная времени, обратная граничной частоте транзистора по крутизне 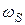 :
:
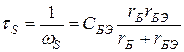 . (5)
. (5)
Для элементов матрицы 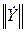 теперь приведем приближенные формулы без вывода:
теперь приведем приближенные формулы без вывода:
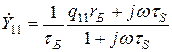 ;
; 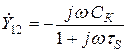 ;
;
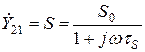 ;
; 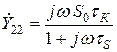 . (6)
. (6)
Правильным являются обозначения 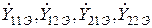 , где буквенный индекс «Э» показывает принадлежность параметра к схеме включения транзистора (ОЭ). Здесь индекс «Э» опущен, так как другие схемы включения в данной работе не рассматриваются.
, где буквенный индекс «Э» показывает принадлежность параметра к схеме включения транзистора (ОЭ). Здесь индекс «Э» опущен, так как другие схемы включения в данной работе не рассматриваются.
Проводимости 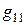 и
и 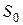 представляют низкочастотные параметры транзистора:
представляют низкочастотные параметры транзистора:
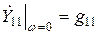 ;
; 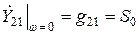 .
.
При определении низкочастотных параметров достаточно мысленно разомкнуть цепи 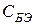 и
и 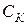 эквивалентной схемы транзистора:
эквивалентной схемы транзистора:
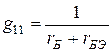 ;
; 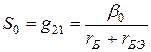 . (7)
. (7)
2.Предварительный анализ усилителя.
Общие выражения, представляющие свойства апериодического усилителя (рис.1), достаточно громоздки. Поэтому для описания свойств такого усилителя используются специфические приёмы. Эти приёмы поясняет частный случай, к анализу которого мы переходим.
Предположим, что падением переменного напряжения на конденсаторах 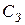 и
и 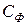 можно пренебречь. Тогда цепи этих конденсаторов можно считать закороченными для переменных токов. Далее, предположим, что используемый транзистор безынерционен (
можно пренебречь. Тогда цепи этих конденсаторов можно считать закороченными для переменных токов. Далее, предположим, что используемый транзистор безынерционен (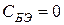 ,
, 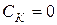 ). Эквивалентная схема каскада для этого случая показана на рис.3.
). Эквивалентная схема каскада для этого случая показана на рис.3.
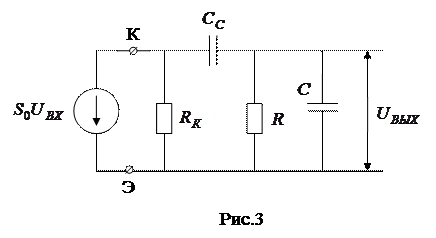 |
Здесь цепь потребителя (Z) составлена из включенных параллельно R и C. Транзистор на схеме отображён генератором тока 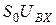 , управляемый переменным входным напряжением
, управляемый переменным входным напряжением 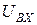 (выходная проводимость этого генератора
(выходная проводимость этого генератора 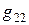 принята равной нулю), а все остальные элементы вместе являются его нагрузкой (
принята равной нулю), а все остальные элементы вместе являются его нагрузкой (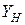 ).
).
Найдём комплексный коэффициент усиления по напряжению для рассматриваемого случая 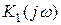 ; представляющий отношение выходного напряжения
; представляющий отношение выходного напряжения 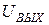 к входному
к входному 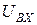 для разных частот:
для разных частот:
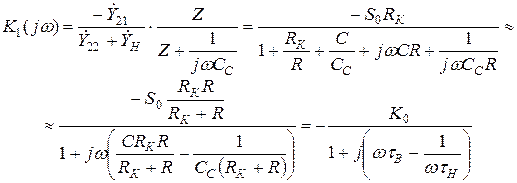 (8)
(8)
Правый сомножитель учитывает, что выходное напряжение является частью напряжения нагрузки из-за падения напряжения на разделительном конденсаторе.
Сделанное приближение
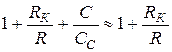
справедливо, так как обычно 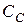 выбирается на несколько порядков больше С. Окончательная запись полученной формулы использует следующие обозначения:
выбирается на несколько порядков больше С. Окончательная запись полученной формулы использует следующие обозначения:
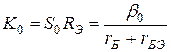 ; (9)
; (9) 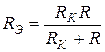 ; (10)
; (10)
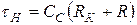 ; (11)
; (11)
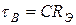 . (12)
. (12)
Из (8) видно, что 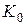 представляет усиление на частоте
представляет усиление на частоте  , называемой средней частотой, при которой
, называемой средней частотой, при которой 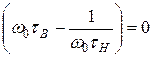 .
.
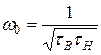 . (13)
. (13)
Знак минус перед 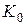 в формуле (8) показывает, что на средней частоте входной и выходной сигналы имеют противоположные полярности.
в формуле (8) показывает, что на средней частоте входной и выходной сигналы имеют противоположные полярности.
По мере удаления от  в обе стороны становятся заметными частотные искажения амплитуды и фазы. При описании этих искажений удобно использовать характерное для апериодических усилителей неравенство
в обе стороны становятся заметными частотные искажения амплитуды и фазы. При описании этих искажений удобно использовать характерное для апериодических усилителей неравенство 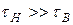 :
:
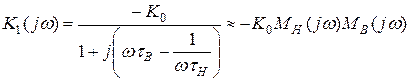 , (14)
, (14)
где
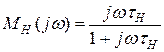 (15)
(15)
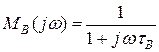 (16)
(16)
Преобразуя (14)
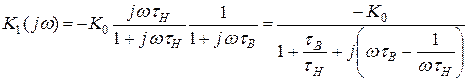
убеждаемся, что при 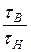 <<1 выражения (8) и (14) практически совпадают.
<<1 выражения (8) и (14) практически совпадают.
Из двух зависящих от частоты сомножителей (14) один проявляет себя тогда, когда другой фактически равен единице. На низких частотах (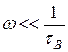 ) в единицу обращается
) в единицу обращается 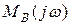 и частотные искажения усилителя описывает
и частотные искажения усилителя описывает 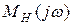 ; на высоких частотах (
; на высоких частотах (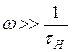 ) единицей становится
) единицей становится 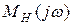 и частотные искажения усилителя представляет
и частотные искажения усилителя представляет 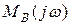 .
.
Раздельное рассмотрение частотных искажений усилителя на низких и высоких частотах составляет существо специфических приёмов апериодического усилителя (рис.1), о которых говорилось выше. Эти приемы используют также для анализа других схем апериодических усилителей.
Сопоставим выражения (15), (16) и (9) с эквивалентной схемой рис.3. На низких частотах велико падение напряжения на разделительном конденсаторе, а шунтирующие действие ёмкости потребителя невелико. Мысленно разомкнув на рис.3 цепь ёмкости потребителя С, получим так называемую эквивалентную схему усилителя для низких частот. Нагрузкой транзистора на этой эквивалентной схеме оказывается дифференцирующая цепочка с постоянной времени 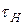 (11). Выражение (15) является частотной характеристикой этой дифференцирующей цепочки. На высоких частотах заметно шунтирующее действие ёмкости потребителя, а падение напряжения на разделительном конденсаторе близко к нулю. Мысленно закоротив на рис.3 цепь разделительного конденсатора
(11). Выражение (15) является частотной характеристикой этой дифференцирующей цепочки. На высоких частотах заметно шунтирующее действие ёмкости потребителя, а падение напряжения на разделительном конденсаторе близко к нулю. Мысленно закоротив на рис.3 цепь разделительного конденсатора 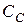 , приходим к так называемой эквивалентной схеме усилителя для высоких частот. Нагрузкой транзистора на высоких частотах оказывается интегрирующая цепочка с постоянной времени
, приходим к так называемой эквивалентной схеме усилителя для высоких частот. Нагрузкой транзистора на высоких частотах оказывается интегрирующая цепочка с постоянной времени 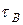 (12). Формула (16) является частотной характеристикой этой интегрирующей цепочки. На средней частоте падение напряжения на разделительном конденсаторе уже близко к нулю, а шунтирующее действие ёмкости потребителя ещё не проявляется. Мысленно закоротив на рис.3 цепь
(12). Формула (16) является частотной характеристикой этой интегрирующей цепочки. На средней частоте падение напряжения на разделительном конденсаторе уже близко к нулю, а шунтирующее действие ёмкости потребителя ещё не проявляется. Мысленно закоротив на рис.3 цепь 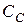 и разомкнув цепь С, найдём эквивалентную схему усилителя для средней частоты.
и разомкнув цепь С, найдём эквивалентную схему усилителя для средней частоты.
Коэффициент усиления 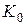 (9) представляет усиление этой эквивалентной схемы, так как нагрузкой транзистора теперь является сопротивление
(9) представляет усиление этой эквивалентной схемы, так как нагрузкой транзистора теперь является сопротивление 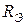 (10).
(10).
Раздельное рассмотрение искажений усилителя на разных частотах основывается на предварительной оценке влияния реактивных элементов и составлении эквивалентных схем. Построенные таким образом схемы позволяют наиболее просто изучить влияние элементов усилителя на усилительные свойства каскада. Предварительная оценка влияния реактивных элементов обычно не вызывает затруднений. Так, ёмкость фильтра и ёмкость в цепи эмиттера проявляют себя на низких частотах, а ёмкости переходов транзистора – на высоких. Поэтому в дальнейшем учёт емкостей 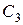 и
и 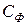 ведётся с использованием низкочастотных параметров транзистора (7), а при учёте инерционности транзистора падение напряжения на конденсаторах
ведётся с использованием низкочастотных параметров транзистора (7), а при учёте инерционности транзистора падение напряжения на конденсаторах 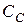 ,
, 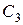 и
и 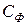 принято равным нулю.
принято равным нулю.
Мерой частотных искажений амплитуды, возникающих при усилении, являются значения нормированной АЧХ усилителя. Используя (14), (15) и (16), найдём нормированную АЧХ для рассматриваемого случая:
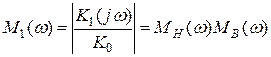 (17)
(17)
Здесь
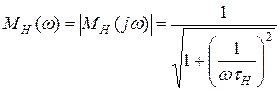 (18)
(18)
и
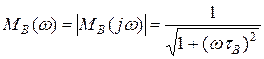 (19)
(19)
График 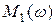 показан на рис.4.
показан на рис.4.
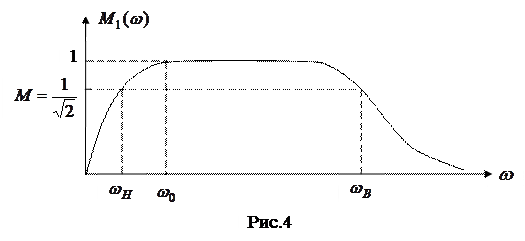 |
Частоты, на которых усиление уменьшается до заданной (допустимой) величины относительно величины 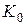 , называют граничными. В дальнейшем заданное уменьшение принято равным
, называют граничными. В дальнейшем заданное уменьшение принято равным 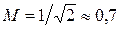 . Из (18) и (19) найдем соответственно нижнюю
. Из (18) и (19) найдем соответственно нижнюю 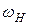 и верхнюю
и верхнюю 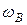 граничные частоты:
граничные частоты:
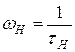 (20)
(20)
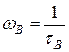 (21)
(21)
У апериодических усилителей 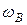 значительно превосходит
значительно превосходит 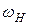 :
:
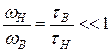 (22)
(22)
Фазовые искажения усилителя представляет ФЧХ. ФЧХ может быть определена из (14), (15) и (16). Рекомендуем учащимся самостоятельно получить и проанализировать выражение для ФЧХ.
3.Влияние цепей эмиттера и фильтра на низких частотах.
В этом и следующем параграфах уточняются полученные ранее характеристики апериодического усилителя (рис.1) в области низких частот.
Влияние цепи эмиттера (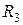 ,
, 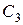 ) на усилительные свойства каскада связано с появлением напряжения обратной связи
) на усилительные свойства каскада связано с появлением напряжения обратной связи 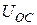 на низких частотах. Для математического описания действия обратной связи по цепи эмиттера обратимся к рис.5.
на низких частотах. Для математического описания действия обратной связи по цепи эмиттера обратимся к рис.5.
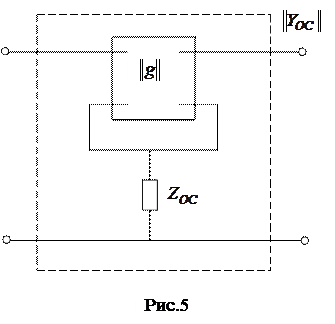 |
Четырехполюсник 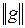 , представляющий транзистор на низких частотах, и сопротивление обратной связи (
, представляющий транзистор на низких частотах, и сопротивление обратной связи (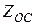 ), включённое в общий провод, образуют новый четырехполюсник, матрицу которого будем обозначать
), включённое в общий провод, образуют новый четырехполюсник, матрицу которого будем обозначать 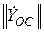 . Элементы матрицы этого нового четырехполюсника можно найти по формулам:
. Элементы матрицы этого нового четырехполюсника можно найти по формулам:
 ;
; 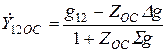
(23)
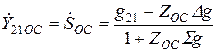 ;
; 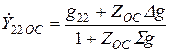
Здесь 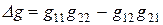 и
и 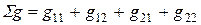 .
.
Поскольку 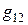 и
и 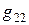 приняты равными нулю, формулы (23) упрощаются:
приняты равными нулю, формулы (23) упрощаются:
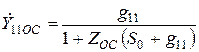 ;
; 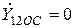 ;
;
(24)
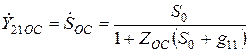 ;
; 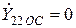 .
.
Возвращаясь к эквивалентной схеме усилителя, приведённой на рис. 3 и заменив в ней 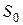 на
на 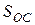 , можно найти коэффициент усиления каскада, учитывающий действие обратной связи по цепи эмиттера. Если при этом исключить частотные зависимости, изученные ранее, будет видно влияние цепи обратной связи, взятой в отдельности. Для этого нагрузку транзистора следует взять равной
, можно найти коэффициент усиления каскада, учитывающий действие обратной связи по цепи эмиттера. Если при этом исключить частотные зависимости, изученные ранее, будет видно влияние цепи обратной связи, взятой в отдельности. Для этого нагрузку транзистора следует взять равной 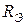 (как на средних частотах).
(как на средних частотах).
Коэффициент усиления, учитывающий только влияние цепи эмиттера 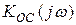 , при этом оказывается равным
, при этом оказывается равным
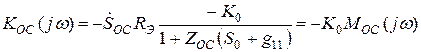
Сравнивая (24) и (25) видим, что частотная зависимость 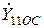 ,
, 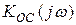 и
и 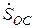 от действия обратной связи по цепи эмиттера во всех случаях одинакова (
от действия обратной связи по цепи эмиттера во всех случаях одинакова (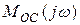 ). Каково физическое содержание этой частотной зависимости?
). Каково физическое содержание этой частотной зависимости?
По закону Кирхгофа
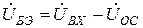 (26)
(26)
В отсутствие обратной связи (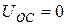 ) весь входной сигнал (
) весь входной сигнал (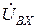 ) подводится к транзистору для усиления. При появлении напряжения обратной связи (
) подводится к транзистору для усиления. При появлении напряжения обратной связи (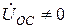 ) транзистор усиливает не весь входной сигнал усилителя (так как
) транзистор усиливает не весь входной сигнал усилителя (так как 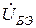 становится меньше
становится меньше 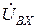 ), а лишь некоторую его часть. Можно показать, что вследствие обратной связи крутизна, входная проводимость и коэффициент усиления уменьшаются во столько раз, во сколько раз на данной частоте
), а лишь некоторую его часть. Можно показать, что вследствие обратной связи крутизна, входная проводимость и коэффициент усиления уменьшаются во столько раз, во сколько раз на данной частоте 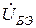 меньше
меньше 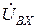 :
:
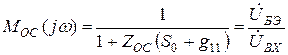 (27)
(27)
Выражение (27) можно преобразовать к виду
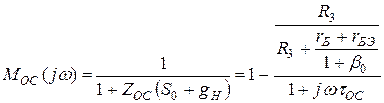 (28)
(28)
откуда следует, что частотная зависимость, вносимая обратной связью по цепи эмиттера, характеризуется параметром 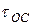 , имеющим смысл постоянной времени:
, имеющим смысл постоянной времени:
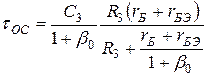 (29)
(29)
В апериодических усилителях обычно
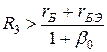 (30)
(30)
Поэтому выражения (28) и (29) можно упростить:
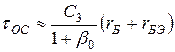 (31)
(31)
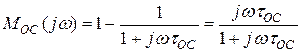 (32)
(32)
Используем эти результаты в (25)
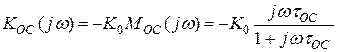 (33)
(33)
После чего можно найти нормированную АЧХ:
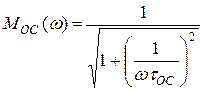 (34)
(34)
Сравнение (15) и (32), а также (18) и (34) показывает на качественное совпадение действия цепей связи и эмиттера. Поэтому можно говорить о нижней граничной частоте от цепи эмиттера 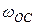 :
:
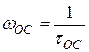 (35)
(35)
Действие цепи связи будет преобладать над действием цепи эмиттера, если 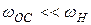 или если будет выполняться неравенство
или если будет выполняться неравенство
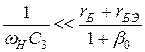 (36)
(36)
Условие (36) часто ошибочно заменяют менее жестким требованием:
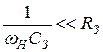
Однако из-за малости правой части, это неравенство обычно не выполняется.
В приведенных выше соотношениях рассматривалось усиление по напряжению. В ряде случаев более показательным является так называемый коэффициент усиления по ЭДС:
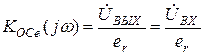 ;
; 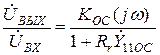 (37)
(37)
Здесь еr – ЭДС генератора сигнала, а Rr – его выходное сопротивление. Величина 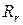 должна учитывать делитель
должна учитывать делитель 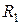 ,
, 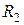 в цепи базы.
в цепи базы.
С учетом (30) характер частотных зависимостей по ЭДС остается таким же, как в (33) и (34). Изменяются только параметры 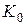 и
и 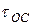 , переходя соответственно в
, переходя соответственно в 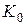 и
и 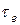 :
:
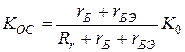 (38)
(38)
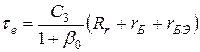 (39)
(39)
Например:
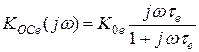 (40)
(40)
Сравнение (9) и (38) показывает, что усиление по ЭДС падает с ростом сопротивления генератора сигнала. В то же время, из (32) и (39) видно, что учет генератора сигнала снижает требования к величине емкости в цепи эмиттера (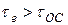 ). Для выбора
). Для выбора 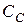 и
и 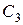 сравним также (11) и (39).
сравним также (11) и (39).
Обычно сопротивления 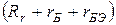 и (
и (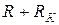 ) одного порядка. Поэтому при выборе емкостей решающим оказывается уменьшение постоянной времени
) одного порядка. Поэтому при выборе емкостей решающим оказывается уменьшение постоянной времени 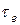 в (1 + b 0) раз от действия обратной связи. Для того чтобы влияние цепи эмиттера не было подавляющим, приходится увеличивать С 3 в десятки раз по сравнению с
в (1 + b 0) раз от действия обратной связи. Для того чтобы влияние цепи эмиттера не было подавляющим, приходится увеличивать С 3 в десятки раз по сравнению с 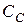 .
.
Результирующая АЧХ по ЭДС для низких частот 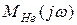 , учитывающая одновременное действие цепей связи и эмиттера, рассчитывается по формуле:
, учитывающая одновременное действие цепей связи и эмиттера, рассчитывается по формуле:
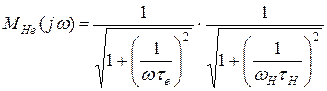 (41)
(41)
Если во входную цепь усилителя последовательно включить сопротивление, имитирующее выходное сопротивление реального генератора сигнала, то зависимость (41) может быть проверена экспериментально.
Проследим теперь влияние цепи фильтра 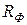 ,
, 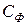 , взятое в отдельности. Для этого вновь обратимся к эквивалентной схеме каскада на средних частотах, дополнив ее цепочкой
, взятое в отдельности. Для этого вновь обратимся к эквивалентной схеме каскада на средних частотах, дополнив ее цепочкой 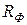 ,
, 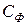 , как это сделано на рис.6 (внутреннее сопротивление источника питания за малостью не учитывается).
, как это сделано на рис.6 (внутреннее сопротивление источника питания за малостью не учитывается).
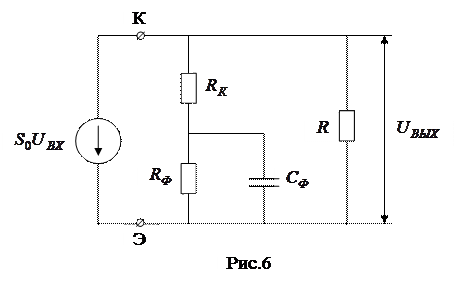 |
Запишем коэффициент усиления этой схемы 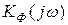 при холостом ходе усилителя (R = ¥):
при холостом ходе усилителя (R = ¥):
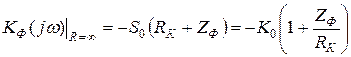 (42)
(42)
Отсюда видно, что 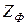 , представляющее параллельное соединение
, представляющее параллельное соединение 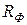 и
и 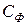 , увеличивает реальную нагрузку в цепи коллектора транзистора, а вместе с ней усиление на низких частотах. Усиление растет с уменьшением
, увеличивает реальную нагрузку в цепи коллектора транзистора, а вместе с ней усиление на низких частотах. Усиление растет с уменьшением 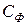 и имеет предел:
и имеет предел:
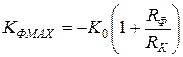 (43)
(43)
С ростом частоты конденсатор 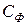 все сильнее шунтирует
все сильнее шунтирует 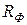 , пока величина усиления не снизится до
, пока величина усиления не снизится до 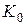 . Таким образом, влияние цепи фильтра проявляется на низких частотах, причем ее действие повышает усиление, т.е. противоположно действию цепей связи и эмиттера. Этим часто пользуются для коррекции искажений на низких частотах.
. Таким образом, влияние цепи фильтра проявляется на низких частотах, причем ее действие повышает усиление, т.е. противоположно действию цепей связи и эмиттера. Этим часто пользуются для коррекции искажений на низких частотах.
4.Учет инерционности транзистора
Запишем общую формулу для коэффициента усиления по напряжению K (jw) через проводимости транзистора и нагрузки:
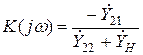 (44)
(44)
Все ранее полученные выражения коэффициентов усиления по напряжению являются частными случаями (44), полученными в предположении, что транзистор безынерционен 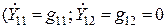 ;
; 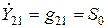 ;
; 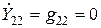 ). На высоких частотах такие упрощения недопустимы. Используя (6) и полагая нагрузку, как у эквивалентной схемы для высоких частот, найдем коэффициент усиления
). На высоких частотах такие упрощения недопустимы. Используя (6) и полагая нагрузку, как у эквивалентной схемы для высоких частот, найдем коэффициент усиления 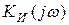 c учетом инерционности транзистора:
c учетом инерционности транзистора:
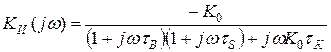 (45)
(45)
Дополнив эквивалентную схему транзистора (рис.2) нагрузкой усилителя для высоких частот, легко проследить частные случаи (45), полагая попеременно С =0 (т.е. 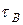 =0),
=0), 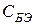 =0 (т.е.
=0 (т.е. 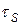 =0) или
=0) или 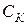 =0 (т.е.
=0 (т.е. 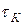 =0).
=0).
Так, частный случай С =0, 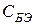 =0,
=0, 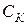 ¹0 показывает, что влияние постоянной времени коллекторной цепи (
¹0 показывает, что влияние постоянной времени коллекторной цепи (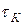 ) зависит от усиления (
) зависит от усиления (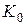 ): с ростом усиления растет выходное напряжение, что приводит к увеличению тока через
): с ростом усиления растет выходное напряжение, что приводит к увеличению тока через 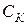 ; ток через
; ток через 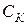 создает на собственно эмиттерном переходе падение напряжения, по знаку противоположное падению напряжения от усиливаемого сигнала.
создает на собственно эмиттерном переходе падение напряжения, по знаку противоположное падению напряжения от усиливаемого сигнала.
Вместо (45) на практике пользуются упрощенной формулой:
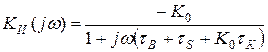 (46)
(46)
Эта формула позволяет определить верхнюю граничную частоту каскада 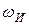 с запасом:
с запасом:
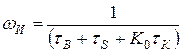 (47)
(47)
Итак, частотные искажения, вносимые усилительным каскадом на высоких частотах, отличаются от найденных при предварительном анализе лишь качественно. Поэтому для описания этих искажений могут быть использованы формулы (16), (19) и (21), если в них заменить 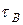 (12) на (
(12) на (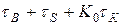 ).
).
Исследование более сложных вопросов работы на высоких частотах, таких как расчет входной проводимости, определение усиления по ЭДС или работа на аналогичный каскад, выходят за рамки данного руководства.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
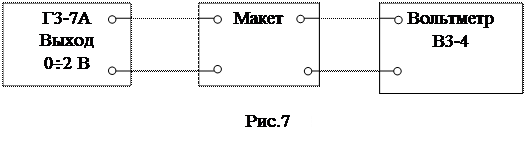
Установка состоит из макета исследуемого усилителя, измерительной аппаратуры и блока питания. Измерительная аппаратура включает звуковой генератор ГЗ-7А и катодный вольтметр (А4-М2 или ВЗ-3). Блок-схема одного из макетов исследуемого усилителя показана на рис.7. назначение переключателей студенты могут проследить самостоятельно.
 |
СОДЕРЖАНИЕ ЭКСПЕРИМЕНТА
1. Снять амплитудные характеристики усилителя для разных нагрузок, построить графики и определить по ним коэффициенты усиления 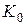 ; выбрать амплитуду сигнала для последующих измерений (вблизи середины линейного участка).
; выбрать амплитуду сигнала для последующих измерений (вблизи середины линейного участка).
2. Экспериментально исследовать влияние элементов усилителя на частотную характеристику:
а) сопротивления нагрузки;
б) емкости разделительного конденсатора;
в) емкости в цепи эмиттера;
г) емкости нагрузки;
д) емкости фильтра.
По результатам эксперимента на одном графике построить нормированные АЧХ.






