Общие указания по изучению курса
И выполнению контрольных работ
В современном обществе статистика является одним из важнейших инструментов управления национальной экономикой. Развитие рыночных отношений в стране поставило перед статистикой новую задачу – реформирование общеметодологических и организационных основ статистической теории и практики. Улучшение хозяйственного руководства неразрывно связано с возрастанием роли статистики и повышением научного уровня статистических исследований.
Главная задача статистики – исчисление и анализ статистических показателей, благодаря чему органы управления получают всестороннюю характеристику управляемых объектов от национальной экономики до подразделений предприятия.
Для составления точного и объективного представления о состоянии и развитии народного хозяйства в целом или отдельных его отраслей, для изучения хозяйственной деятельности и ее результатов необходимы систематизация и обобщение данных об отдельных фактах и явлениях данной отрасли. Наблюдение (учет) отдельных фактов, их систематизация и обобщение выполняются особыми методами на основе использования соответствующей системы понятий и показателей. Эти понятия, показатели и методы разрабатывает особая наука – общая теория статистики. Она устанавливает, как собирать данные об отдельных случаях изучаемого явления, как вести обработку этих данных для получения выраженных в числовой форме обобщающих (статистических) показателей по явлению в целом, как изучать и анализировать полученный таким образом материал.
Для изучения курса необходимо изучить литературу, рекомендованную в данных методических указаниях.
Для закрепления полученных знаний и выработки навыков по расчету статистических показателей студентам необходимо выполнить контрольную работу.
Варианты выбираются в соответствии с первой буквой фамилии и последней цифрой шифра зачетной книжки. По каждому варианту студенту предлагается решить шесть задач.
Решение задач должно сопровождаться приведением формул расчета, а также выводов из произведенных расчетов.
Требования к выполнению контрольных работ:
– работа должна быть выполнена в отдельной тетради;
– с правой стороны должны быть оставлены поля для замечаний преподавателя;
– решение каждой задачи должно содержать ее условие;
– в заключении должен быть приведен список использованной литературы, оформленный в соответствии с требованиями;
– после списка литературы ставится дата и подпись студента.
Распределение задач по вариантам
| Первая буква фамилии | Последняя цифра шифра зачетной книжки | |||||||||
| А, Б, В, Г, Д, е, Ж | 1, 11, 21, 31, 41, 51 | 2, 12, 22, 32, 42, 52 | 3,13, 23, 33, 43, 53 | 4, 14, 24, 34, 44, 54 | 5, 15, 25, 35, 45, 55 | 6, 16, 26, 36, 46, 56 | 7, 17, 27, 37, 47, 57 | 8, 18, 28, 38, 48, 58 | 9, 19, 29, 39, 49, 59 | 10, 20, 30, 40, 50, 60 |
| З, И, К, Л, М, Н, о | 6, 14, 22, 32, 43, 57 | 8, 15, 23, 33, 44, 58 | 9, 16, 24, 34, 45, 59 | 10, 17, 25, 35, 46 | 1, 18, 26, 36, 47, 60 | 2, 19, 27, 37, 48, 51 | 3, 20, 28, 38, 49, 52 | 4, 11, 29, 39, 50, 53 | 5, 12, 30, 40, 44, 58 | 6, 13, 21, 24, 45, 59 |
| П, Р, С, Т, У, Ф, Х | 9, 14, 22, 38, 46, 60 | 7, 15, 23, 39, 47, 51 | 1, 16, 24, 37, 48, 52 | 2, 17, 25, 31, 49, 53 | 3, 18, 26, 39, 50, 54 | 4, 19, 27, 32, 41, 55 | 5, 20, 28, 34, 42, 56 | 6, 12, 29, 33, 43, 57 | 7, 13, 30, 41, 44, 58 | 8, 14, 21, 33, 45, 59 |
| Ц, Ч, Ш, Щ, Э, Ю, Я | 2, 15, 22, 35, 46, 60 | 10, 16, 23, 36, 47, 51 | 8, 17, 24, 37, 48, 52 | 3, 18, 25, 38, 49, 53 | 4, 19, 26, 39, 50, 54 | 5, 20, 27, 40, 41, 55 | 6, 11, 28, 32, 44, 56 | 7, 12, 29, 33, 45, 57 | 8, 13, 30, 34, 46, 58 | 9, 14, 25, 36, 47, 59 |
Тема 1 АБСОЛЮТНЫЕ, ОТНОСИТЕЛЬНЫЕ
И СРЕДНИЕ ПОКАЗАТЕЛИ
АБСОЛЮТНЫЕ ВЕЛИЧИНЫ
Статистическое изучение отдельных производственных процессов неразрывно связано с необходимостью измерения каждого явления, процесса, отображения их в абсолютных объемных показателях и характеристики явлений или процессов системой относительных и средних величин.
Абсолютные величины выражают объемы или размеры социально-экономических явлений в определенных границах места и времени. Так, по автотранспортному предприятию устанавливаются объем перевозок в тоннах, общая сумма затрат на перевозки, объем доходов и прибыли в тыс. руб. и т. д.
Статистические абсолютные величины – числа именованные, они выражают объемы явлений и процессов в определенных единицах измерения. Выбор единиц измерения зависит от характера изучаемого явления и задач исследования. Единицы измерения могут быть натуральными (численность, меры веса, объема, длины и т. д.), условными натуральными, трудовыми и стоимостными.
Натуральные единицы – бывают простыми и составными (комбинированными). Например, объем грузовых перевозок измеряется количеством перевезенных тонн груза, а грузооборот (объем транспортной работы при перевозке грузов – в тонно-километрах: в первом случае натуральная единица измерения простая, во втором – комбинированная.
Достаточно широкое применение имеют абсолютные величины, выраженные в условно-натуральных единицах измерения. Они используются для получения общего итога производства или потребления нескольких видов продукции. Например, общий расход нескольких видов топлива выражается в тоннах условного топлива с учетом теплотворной способности различных видов топлива.
Трудовые единицы (человеко-час, человеко-день) используются для определения общих затрат труда на производство продукции, выполнение какой-либо работы.
В стоимостных единицах измерения (тыс. руб. и т. д.) характеризуются: общий объем продукции предприятия, отрасли, национальный доход страны. Общий результат работы автотранспортных предприятий также выражается в денежных единицах и называется общим объемом доходов.
ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
В научном анализе для раскрытия явления, выявления определенных закономерностей, разносторонней характеристики изучаемого явления приходится прибегать к сопоставлению абсолютных показателей друг с другом и исчислению на этой основе относительных и средних величин.
Относительные показатели получают в результате сравнения двух абсолютных величин. В числителе стоит сравниваемая величина, а в знаменателе – база сравнения.
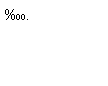Если база сравнения приравнивается к единице – единицей измерения будет коэффициент; если к 100 – процент %; если к 1000 – промилле ‰; если к 10000 – продецимилле
Основным условием правильного расчета относительных величин является сопоставимость сравниваемого показателя.
В соответствии с различными задачами и направлениями сопоставления статистических данных различают несколько видов относительных величин.
Виды относительных величин:
1. Относительная величина планового задания представляет собой отношение уровня по плану на предстоящий (отчетный) период к фактическому уровню показателя в базисном периоде.
;
2. Относительная величина выполнения плана – это отношение фактического уровня показателя в отчетном периоде к плановому уровню показателя того же отчетного периода.
;
3. Относительная величина динамики – это отношение фактического уровня показателя отчетного периода к фактическому уровню показателя базисного периода.
; 
Эти виды относительных величин взаимосвязаны между собой:
ОПД=ОППЗ×ОПВП
4. Относительная величина структуры – характеризует долю, которую занимает каждая группа во всей совокупности и исчисляется отношением объема отдельной единицы совокупности к объему всей совокупности.
5. Относительная величина координации характеризует соотношение отдельных частей целого между собой (соотношение мужчин и женщин)
6. Относительная величина интенсивности характеризует степень распространения какого-либо явления в определенной среде (приходится врачей на 1000 человек населения, коэффициент рождаемости, смертности):
7. Относительная величина уровня экономического развития характеризует производство или потребление продукции в расчете на душу населения
8. Относительная величина сравнения – это соотношение одноименных абсолютных показателей, относящихся к одному и тому же периоду времени, но к разным объектам (производство молока в Пензенской области по сравнению с производством молока в Саратовской области, Ульяновской).
СРЕДНИЕ ВЕЛИЧИНЫ
Особое место среди обобщающих показателей занимают средние величины. С помощью средней величины можно одним числом охарактеризовать уровень изучаемого признака для всей совокупности.
Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени.
Средние, применяемые в статистике, могут принимать две формы: простую и взвешенную.
В экономических исследованиях и плановых расчетах применяется несколько видов средних величин, которые относятся к классу степенных средних и объединяются общими формулами (при различных значениях к):
| Простая степенная средняя | Взвешенная степенная средняя |
| 
|
где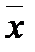 
– среднее значение исследуемого явления; к – показатель степени средней; х – текущее значение (вариант) осредняемого признака; n – число единиц совокупности; f – число единиц в i -ой группе.
В зависимости от значения показателя степени к различают следующие виды степенных средних:
При к = 1 – средняя арифметическая;
При к = 2 – средняя квадратическая;
При к = 0 – средняя геометрическая;
При к = –1 – средняя гармоническая.
| Средние показатели |
| Средняя арифметическая |
| Средняя гармоническая |
Средняя хронологическая
|
Средняя арифметическая простая
|
Средняя арифметическая взвешенная
|
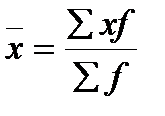
Средняя гармоническая простая
|
Средняя гармоническая взвешенная
|
Средняя геометрическая
 или
|
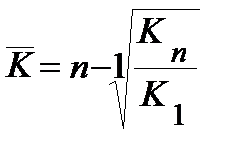
Рисунок 1 – Виды средних величин
Чтобы правильно выбрать форму средней, используется специальный критерий, который называется логической формулой средней:
Кроме них используются структурные средние – мода; медиана.
Мода и медиана рассчитывается в дискретном и интервальном ряду.
Мода – это численное значение признака, которое наиболее часто встречается в статистическом ряду.
Медиана – это численное значение признака, которое находится в середине ранжированного ряда (расположенного в порядке возрастания или убывания) и делит этот ряд на две равные по численности части.
Если дискретный ряд имеет нечетное значение членов, то медианой будет варианта, находящаяся в середине ранжированного ряда. Если ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Мода в дискретном вариационном ряду находится без каких-либо расчетов, для этого надо отыскать наибольшую частоту и варианту, которой она соответствует.
| Структурные средние |
| Мода |
| Медиана |
| В дискретном ряду распределения |
| В интервальном ряду распределения |
| В дискретном ряду распределения |
| В интервальном ряду распределения |
|
|
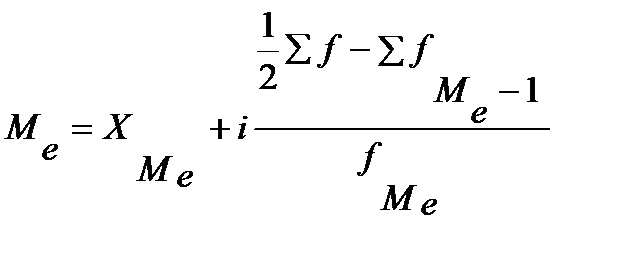
Рисунок 2 – Классификация структурных средних
где М0 – модальное значение признака; ХМ0 – нижняя граница модального интервала; i – величина интервала; fM0 – частота модального интервала; fM0-1 – частота предмодального интервала; fM0+1 – частота послемодального интервала.
Ме – медиана; ХМе – нижняя граница медианного интервала;
i – величина интервала; 
f – общая сумма частот; fMе – частота медианного интервала.
Тема 2 Показатели вариации
Для углубленного анализа той или совокупности средняя должна дополняться показателями вариации, то есть показателями отклонений индивидуальных единиц совокупности от средней.
Вариацией называется различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.
Статистический анализ вариации предполагает выполнение следующих этапов:
1. Построение вариационного ряда;
2. Графическое изображение вариационного ряда;
3. Расчет показателей центра распределения и структурных характеристик вариационного ряда;
4. Расчет показателей размера и интенсивности вариации;
Построение вариационного ряда (ряда распределения) – это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным его значением.
В составе любого вариационного ряда можно выделить три основных элемента: варианты, частоты, частости.
Варианты – это значения, которые принимает исследуемый признак (x). Если варианты представлены в виде целочисленных величин, вариационный ряд называют дискретным, если в виде интервалов – интервальным.
Частоты вариационного ряда – абсолютная численность отдельных групп с различными значениями признака (f).
Частости – удельные веса (доли) отдельных групп в общей численности совокупности (w):
Вариация, порождаемая существенными факторами, носит систематический характер и называется систематической вариацией.
Вариация, обусловленная случайными факторами, называется случайной вариацией. Здесь не наблюдается систематического изменения вариант от случайных факторов.
Вариация, образовавшаяся под действием всех без исключения факторов, влияющих на результат, называется общей вариацией.
Все показатели вариации делятся на:
1. Показатели центра распределения – средняя арифметическая, мода и медиана.
2. Показатели степени распределения – размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
3. Показатели типа распределения.
2. Расчет средней величины признака в вариационном ряду осуществляется по формуле средней арифметической:
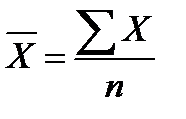
Однако сама по себе средняя арифметическая недостаточна для обобщающей характеристики совокупности. Показатели вариации служат характеристикой типичности самой средней. Чем меньше вариация, тем средняя более типична.
В отличие от средней мода и медиана характеризуют величину варианты, занимающей центральное место в ранжированном ряду (см. тему «Средние величины»).
К структурным средним относятся также квартили, децили и перцентили.
Квартили – значение признака, делящее ранжированную совокупность на четыре равные части. Различают квартили первого порядка (нижний квартиль) и квартиль третьего порядка (верхний квартиль). Каждый из них отсекает соответственно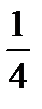 
и 
совокупности. Для расчета квартилей используются следующие формулы:
Децили – варианты, делящие ранжированный ряд на десять равных частей. Первый дециль отсекает 1/10 часть совокупности, а девятый дециль отсекает 9/10 частей. Рассчитываются децили по аналогичным формулам:
Перцентили – варианты, которые делят ранжированную совокупность на 100 частей.
Для измерения вариации признака применяются различные абсолютные и относительные показатели.
1. Размах вариации R = Xmax - Xmin
Этот показатель является приближенной характеристикой совокупности, так как отражает колеблемость лишь крайних значений признака.
Для характеристики средней величины всех отклонений от средней служит:
2. Среднее линейное отклонение
| Простое (для несгруппированных данных) | Взвешенное (для сгруппированных данных) |
| 
|
Недостатком среднего линейного отклонения является то, что не учитываются знаки отклонения. Поэтому для определения общего объема вариации отклонения от средней с разными знаками применяются дисперсия и среднее квадратическое отклонение.
3. Дисперсия – это средняя из квадратов отклонений вариантов значений признака от их средней величины:
| Простая (для несгруппированных данных) | Взвешенная (для сгруппированных данных) |
| 
|
4. Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
| Простое (для несгруппированных данных) | Взвешенное (для сгруппированных данных) |
| 
|
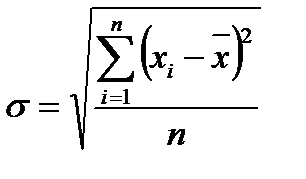
Размах вариации, среднее линейное отклонение и среднее квадратическое отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.
Среднее линейное и среднее квадратическое отклонения показывают на сколько в среднем колеблется величина признака у единиц исследуемой совокупности.
5. Коэффициент вариации
Его используют для сравнения вариации разных совокупностей, а также для характеристики однородности совокупности. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается однородной, если коэффициент вариации не превышает 33 %. При коэффициенте вариации от 30 до 60 % однородность совокупности средняя, при 60 % и более – совокупность неоднородна.
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее сделать расчеты.
Вариация сгруппированных данных оценивается дисперсией. Если совокупность разделена на группы по одному фактору, в ней могут рассматриваться следующие виды дисперсий:
1. общая дисперсия, которая изучает вариацию признака во всей совокупности под влиянием всех факторов:
|
|
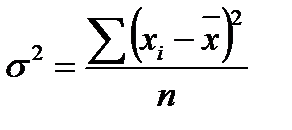
2. Внутригрупповая дисперсия измеряет вариацию признака внутри групп и характеризует вариацию результативного признака под действием всех неучтенных факторов, кроме фактора, положенного в основу группировки:
где: 
– групповая средняя;
ni – объем (численность) i -ой группы
3. Средняя из внутригрупповых дисперсий
,
где: 
– дисперсия результативного признака в i -ой группе;
ni – объем (численность) i -ой группы.
3. Межгрупповая дисперсия измеряет колеблемость групповых средних вокруг общих средних и характеризует систематическую вариацию результативного признака, обусловленную признаком, положенным в основание группировки.
,
где: 
– среднее значение результативного признака по i -ой группе;
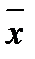– общая средняя по совокупности в целом;
ni – объем (численность) i -ой группы.
Таким образом, вариация под действием всех факторов раскладывается на вариацию, обусловленную систематическими признаками и случайными. И соответственно общая дисперсия равна сумме дисперсий межгрупповой и внутригрупповой:
,
где: 
– общая дисперсия;
– средняя из внутригрупповых дисперсий;
– межгрупповая дисперсия.
На среднее квадратическое отклонение и коэффициент вариации это правило сложения вариации не распространяется.
Чтобы оценить, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки, рассчитывается коэффициент детерминации:
Корень из коэффициента детерминации называется корреляционным отношением и показывает тесноту связи между группировочным и результативным признаком:
Тема 3 РЯДЫ ДИНАМИКИ
Все явления природы и общества находятся в постоянном движении и развитии. Те из них, которые поддаются количественному измерению, изучаются путем построения и анализа рядов динамики.
Ряд динамики – это временная последовательность статистических показателей.
Каждый временной ряд состоит из двух элементов: 1) моменты или периоды времени; 2) статистические показатели, которые характеризуют изучаемый объект на определенный момент или за указанный период времени.
Статистические показатели, характеризующие изучаемый объект, называют уровнями ряда.
| Динамические ряды |
| Составные элементы динамического ряда |
| Виды динамических рядов |
| По форме представления уровней |
| Уровни или показатели |
| Время или период |
| По времени |
| Моментный |
| Абсолютных величин |
| Относительных величин |
| Интервальный (периодический) |
| Средних величин |
| По расстоянию между датами |
| По числу показателей |
| Полные |
| Неполные |
| Изолированные |
| Комплексные (многомерные) |
Рисунок 3 – Классификация динамических рядов
В зависимости от характера изучаемого явления ряд динамики может отражать его уровень за определенный период времени или на какую-либо дату. В связи с этим различают два вида рядов динамики: моментный и интервальный.
По полноте времени, отраженному в динамических рядах они бывают полные и неполные. В неполных рядах интервалы между моментами времени неодинаковые.
По способу выражения уровней динамические ряды могут быть представлены абсолютными, относительными и средними величинами.
Для изучения интенсивности изменения уровней ряда от срока к сроку исчисляются показатели динамики, которые могут быть рассчитаны с постоянной и переменной базой (цепная и базисная система расчета).
Если каждый последующий уровень сравнивается с предыдущим – это цепная система расчета; а если с базой сравнения – базисная система расчета.
Для записи показателей применяются обозначения:
y1 – начальный уровень динамического ряда
yn – последний уровень ряда
yi – уровни между y1 и yn
n – число уровней ряда
Таблица 1 – Показатели динамики
| Показатели динамики | Условное обозначение | Система расчета | |
| базисная | цепная | ||
| Абсолютный прирост | ∆y | yi – y1 | yi – yi–1 |
| Темп роста | Tр |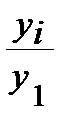 
| 
|
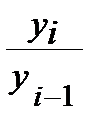
| Темп прироста | Тпр | Тр – 1 | Тр – 1 |
| Абсолютное значение 1 % прироста | А | – | 0,01 yi –1 |
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели динамики, которые также могут быть рассчитаны цепным и базисным методом.
Таблица 2 – Средние показатели динамики
| Средние показатели динамики | Условное обозначение | Система расчета | |
| базисная | цепная | ||
| Средний абсолютный прирост | 
| 
| 
|
| Средний темп роста | 
| 
| 
|
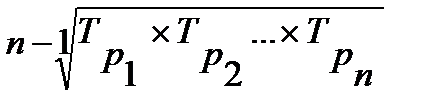
| Средний темп прироста | 
| 
| 
|
Составной частью анализа динамического ряда является выявление тенденции в развитии изучаемого явления.
Основной тенденцией ряда динамики называется устойчивое изменение уровня явления во времени, относительно свободное от случайных колебаний.
Для выявления тенденции применяются следующие основные методы:
- метод укрупнения периодов;
- метод скользящей средней;
- метод аналитического выравнивания.
Метод укрупнения периодов заключается в замене существующих уровней динамического ряда укрупненными уровнями с последующей характеристикой этих периодов средней величиной.
Метод скользящей средней заключается в замене существующих уровней динамического ряда укрупненными периодами при включении в эти периоды одного или нескольких уровней при одновременном исключении из этих периодов одного или нескольких уровней. Вновь полученные периоды также характеризуются средними величинами.
Метод аналитического выравнивания заключается в выражении тенденции развития через определенную математическую функцию (уравнение). Для выравнивания динамического ряда могут быть использованы различные виды функций:
Таблица 3 – Виды функций и их алгебраическое выражение
| Наименование функций | Алгебраические формулы | |
| 1. | Линейная | 
|
| 2. | Квадратическая |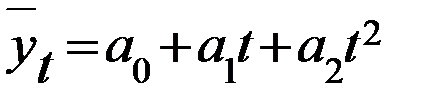 
|
| 3. | Гиперболическая | 
|
| 4. | Степенная |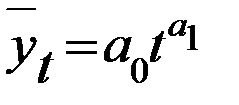 
|
| 5. | Показательная | 
|
где
yt –расчетные (выровненные) значения уровней;
t – порядковый номер года;
a0 – свободный член уравнения;
а1 и а2 – коэффициенты регрессии.
Тема 4 ИНДЕКСЫ
Индексы представляют собой сложные относительные показатели, характеризующие среднее изменение массовых явлений, состоящих из непосредственно несоизмеримых показателей.
По степени охвата явления индексы подразделяют на индивидуальные (охватывают единичные явления) и общие (охватывают все явление целиком, например, сельскохозяйственное предприятие, сельское хозяйство).
По содержанию индексируемых величин различают индексы объемных и качественных показателей.
При необходимости сопоставления более чем двух периодов используют цепные и базисные индексы. Базисными индексами называются те, в которых величины, характеризующие изучаемое явление в последовательные отчетные периоды, сопоставляются все время с величиной, характеризующей явление в одном определенном базисном периоде. Цепными называются индексы, в которых индексируемая величина каждого из отчетных периодов сопоставляется с величиной, характеризующей явление в предыдущем периоде. Между цепными и базисными индексами существует взаимосвязь: произведение цепных индексов равняется последнему базисному.
| Индексы |
| Объемных показателей |
| Качественных показателей |
| Общие |
| Групповые |
| Индивидуальные |
| Агрегатные |
| Средние из индивидуальных |
| Цепные |
| Базисные |
Рисунок 4 – Основные виды индексов
В зависимости от методологии расчета различают:
- агрегатные индексы;
- средние из индивидуальных индексов:
Если информационная база не дает возможности проведения индексного анализа в агрегатной форме, индексы могут быть построены в форме средних из индивидуальных индексов (средний арифметический индекс, средний гармонический индекс).
Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы фиксированного (постоянного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, а в индексах фиксированного состава – на базе неизменной структуры явления.
Таблица 4 – Основные виды индексов
| Название индекса | Индивидуальный индекс | Общий индекс | Средние индексы |
| Индекс цен | 
| 
| 
|
| Индекс физического объема | 
| 
| 
|
| Индекс выручки | 
| 
| |
| Индекс себестоимости | 
| 
| |
| Индекс затрат | 
| 
| |
| Индекс валового сбора сельскохозяйственных культур |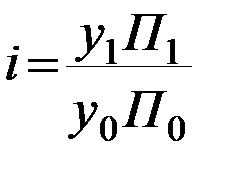 
| 
| |
| Индекс урожайности постоянного состава | 
| ||
| Индекс структурных сдвигов | 
|
Тема 5 Выборочное наблюдение
Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом.
Совокупность отобранных для обследования единиц называют выборочной, а совокупность единиц, из которых производится отбор – генеральной.
По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом – группы единиц, а при комбинированном отборе производится сочетание группового и индивидуального отбора.
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.
Бесповторным называется отбор, при котором попавшая в выборку единица не возвращается в генеральную совокупность. При повторном отборе – попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную совокупность и может снова участвовать в процедуре отбора.
Способ отбора определяет конкретный механизм выборки единиц из генеральной совокупности. Существуют следующие способы отбора:
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад без каких-либо элементов системности.
Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, то есть имеется определенная последовательность в расположении единиц.
Типический отбор используется, когда все единицы генеральной совокупности можно разбить на несколько типических групп.
Серийный отбор удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии, равные по объему. Внутри групп обследуются все без исключения единицы.
В каждом конкретном случае рассчитываются средняя и предельная ошибки выборки, которые позволяют распространить результаты выборочного обследования на генеральную совокупность.
В зависимости от способа отбора используются различные формулы для расчета ошибок (см. таблицу).
Комбинированный отбор предполагает сочетание всех перечисленных способов отбора. Ошибка выборки в этом случае рассчитывается отдельно на каждом этапе.
Для определения необходимой численности выборки задается уровень точности выборочной совокупности с определенной вероятностью. Формула для расчета необходимой численности выборки выводится из формулы предельной ошибки. Поэтому расчет необходимой численности выборки будет осуществляться исходя из способа отбора.
Таблица – Предельная ошибка выборки для различных способов отбора
| Метод отбора Вид выборки | Повторный | Бесповторный | ||
| для средней | для доли | для средней | для доли | |
| Собственно случайная и механическая | 
| 
| 
| 
|
| Типическая |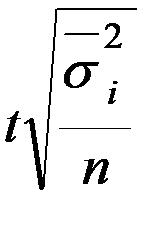 
| 
| 
| 
|
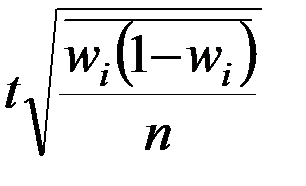
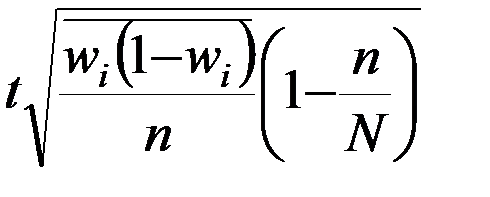
| Серийная | 
| 
| 
| 
|
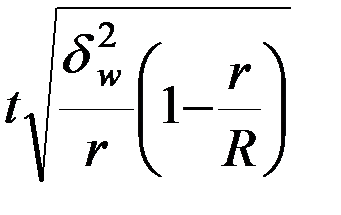
Однако каждая из формул численности показывает, что с увеличением предполагаемой ошибки выборки значительно уменьшается ее необходимый объем. Кроме того, для определения численности выборки необходимо также задать уровень колеблемости, выражаемый дисперсией или средним квадратическим отклонением. Формулы для расчета необходимой численности выборки представлены в таблице. Эти методы расчета численности используются в тех случаях, когда речь идет о количественных признаках.
Способ выражения качественных признаков не позволяет рассчитать по ним средние значения, дисперсию и среднее квадратическое отклонение, поэтому оценка колеблемости производится исходя из долей единиц, обладающих значениями этих признаков, то есть выборочных долей.
Если расчет проводится по качественному альтернативному признаку и не известна его доля в генеральной совокупности, то рекомендуется принять ее равной 0,5. Именно при этом значении дисперсия доли достигает своего максимума 0,25.
Таблица – Необходимый объем выборки для некоторых способов формирования выборочной совокупности
| Виды выборочного наблюдения | Повторный отбор | Бесповторный отбор |
| Собственно-случайная выборка | ||
| При определении среднего размера признака | 
| 
|
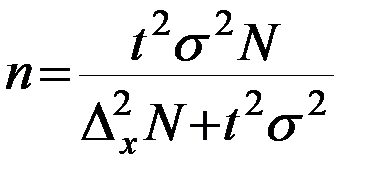
| При определении доли признака | 
| 
|
| Механическая выборка | То же | То же |
| Типическая выборка | ||
| При определении среднего размера признака | 
| 
|
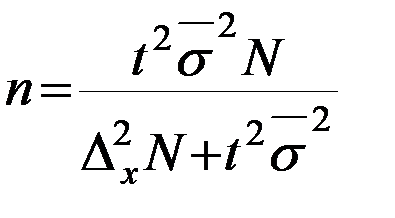
| При определении доли признака | 
| 
|
| Серийная выборка | ||
| При определении среднего размера признака | 
| 
|
| При определении доли признака | 
| 
|
Заключительный этап – распространение результатов выборочного обследования на генеральную совокупность. Вывод о возможности распространения зависит от полноты выборки. Под полнотой понимается наличие или представленность всех типов и групп данной генеральной совокупности в основе выборки.
Более точной основой суждения о распространении результатов является расчет относительной ошибки:
- для средней: 
- для доли: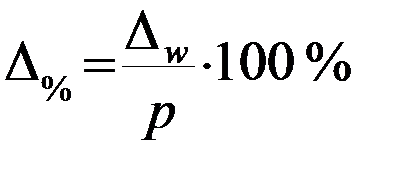 
Если величина относительной ошибки не превышает заранее установленного для данного обследования предельного значения, то данные выборочного наблюдения являются представительными и могут быть распространены на генеральную совокупность.
Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 30.
При оценке результатов малой выборки величина генеральной дисперсии в расчетах не используется. Для определения возможных пределов ошибки пользуются так называемым критерием Стьюдента:
,
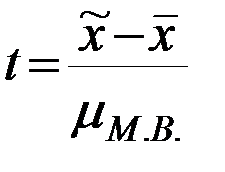где 
– мера случайных колебаний выборочной средней в малой выборке.
Величина s и предельная ошибка малой выборки вычисляются на основе данных выборочного наблюдения:
и 
Но в данном случае вероятная оценка зависит не только от величины t, но и от объема выборки. Величина коэффициента доверия t при различных объемах малой выборки представлена в таблице.
Таблица – Распределение вероятности в малых выборках в зависимости от коэффициента доверия t и объема выборки n
| n t | ∞ | |||||||||
| 0,5 | 0,348 | 0,356 | 0,362 | 0,366 | 0,368 | 0,370 | 0,372 | 0,376 | 0,378 | 0,383 |
| 1,0 | 0,608 | 0,626 | 0,636 | 0.644 | 0,650 | 0,654 | 0.656 | 0,666 | 0,670 | 0.683 |
| 1,5 | 0,770 | 0,792 | 0,806 | 0,816 | 0,832 | 0,828 | 0,832 | 0,846 | 0,850 | 0,865 |
| 2,0 | 0,860 | 0,884 | 0,908 | 0,908 | 0,914 | 0,920 | 0,924 | 0,936 | 0,940 | 0,954 |
| 2,5 | 0,933 | 0,946 | 0,955 | 0,959 | 0,963 | 0,966 | 0,968 | 0,975 | 0,978 | 0,988 |
| 3,0 | 0,942 | 0,960 | 0,970 | 0,976 | 0,980 | 0,938 | 0,984 | 0,992 | 0,992 | 0,997 |
Независимо от вида выборки на заключительном этапе определяются доверительные интервалы, в которых может находиться генеральная средняя (для количественных признаков) или генеральная доля (для качественных признаков).
Доверительные интервалы – это область тех значений генеральной средней, выход за пределы которой имеет весьма малую вероятность. Доверительные интервалы определяются по формулам:
- для средней 
- для доли 
- для малой выборки 
Тема 6 КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
Каждое явление есть следствие многих факторов и причин, и в свою очередь, каждое явление влияет на многие другие явления.
В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины ведет к изменению другого - следствия.
В статистике различают функциональную связь и стохастическую зависимость. Функциональной называют связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Связь, при которой каждому определенному значению влияющего фактора соответствует не одно, а ряд различных, не имеющих строго определенной величины значений рассматриваемого признака. Эти значения колеблются вокруг средней из них. Стохастическая зависимость проявляется только в средних величинах и выражает числовое соотношение между ними в виде тенденции к возрастанию или убыванию одной переменной величины при возрастании или убыванию другой.
Стохастические связи можно классифицировать:
1) по направлению – связи прямые (положительные) и обратные (отрицательные). При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются под воздействием факторного в противоположном направлении по сравнению с изменением факторного признака;
2) по аналитической форме – линейные и нелинейные. Если статистическая связь между явлениями может быть выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии – то нелинейной или криволинейной;
3) по количеству взаимодействующих факторов – парные и множественные. Практическое значение парной линейной корреляции состоит в выделении одного важнейшего фактора, который определяет вариацию результативного признака;
4) по силе – слабые и сильные, теснота которых определяется специальными критериями.
Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками.
Теснота связи количественно выражается величиной коэффициентов корреляции.
Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:
Линейный коэффициент корреляции измеряется в пределах от
–1 до +1.
По степени тесноты связи различают количественные критерии оценки тесноты связи:
| Величина коэффициента корреляции | Характер связи |
| До ±0,3 | Практически отсутствует |
| ±0,3 – ±0,5 | Слабая |
| ±0,5 – ±0,7 | Умеренная |
| ±0,7 – ±1,0 | Сильная |
Чем ближе линейный коэффициент корреляции по абсолютной величине к 1, тем теснее связь. Если он равен 1, то зависимость является не стохастической, а функциональной.
Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение: 
Теоретическое корреляционное отношение рассчитывается по формулам:
С помощью теоретического корреляционного отношения измеряется теснота связи любой формы, а посредством линейного коэффициента корреляции – только прямолинейной связи.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин (факторов).
По форме зависимости различают
- линейную регрессию, которая выражается уравнением прямой (линейной функции) вида: 
- нелинейную регрессию, которая выражается уравнениями вида:
Парабола – 
Гипербола – 
По направлению связи различают:
- прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно уменьшается или увеличивается.
Парная регрессия характеризует связь между двумя признаками: результативным и факторным.
Оценка параметров уравнения регрессии а0 и а1 осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели, при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии:
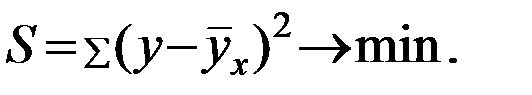
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
где n – объем исследуемой совокупности (число единиц наблюдений).
В уравнениях регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных факторов; параметр а1 – коэффициент регрессии показывает, на сколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.
Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множественной регрессии требуется определить аналитическое выражение связи между результативным признаком (Y) и множеством факторных признаков (х1, х2, х3, … хn).
Практика построения многофакторных моделей показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать, используя пять типов моделей:
- линейная ;
- степенная ;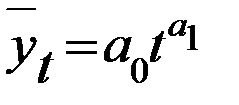
- показательная ;
- параболическая ;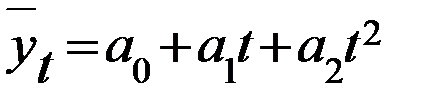
- гиперболическая .
При наличии линейной связи между результативным и несколькими факторными признаками, а также между парой факторных признаков определяется множественный коэффициент корреляции:
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Чем ближе R к единице, тем сильнее связь между признаками.
Часто исследуемые признаки имеют разные единицы измерения, поэтому для оценки влияния факторного признака на результативный применяется коэффициент эластичности. Он рассчитывается для каждой точки и в среднем по всей совокупности по формуле:
где
Коэффициент эластичности показывает, на сколько процентов изменяется результативный признака при изменении факторного
на 1 %.
Чтобы иметь возможность судить о сравнительной связи влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные (средние) коэффициенты эластичности, а также бета-коэффициенты и дельта-коэффициенты.
Различия в единицах измерения факторов устраняют с помощью частных (средних) коэффициентов эластичности, которые рассчитываются по формуле:
где
Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1 % каждого фактора при фиксированном значении других факторов.
Бета-коэффициент используется для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя; необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Он вычисляется по формуле:
где
Бета-коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.
Дельта-коэффициент показывает, какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. Он может быть вычислен по формуле:
где R2 – коэффициент множественной детерминации, который представляет собой квадрат линейного коэффициента корреляции. Его числовое значение всегда заключено в пределах от 0 до 1. Он характеризует долю вариации (разброса) зависимой переменной. Значение коэффициента детерминации непосредственно указывает степень влияния независимого фактора на результативный показатель.
Задачи для контрольной работы
Задача 1
По магазину имеются данные по объему продаж:
| Вид товара | Фактически за 2005 год | 2006 год | ||||||||||
| 1 полугодие | 2 по |
|
|
|
|
|
Дата добавления: 2017-02-25; Мы поможем в написании ваших работ!; просмотров: 431 | Нарушение авторских прав
Лучшие изречения:
| 2072 - 
Ген: 0.015 с.