ЦЕЛЬ РАБОТЫ
Целью работы является:
- знакомство с компьютерным моделированием электрического поля точечных зарядов;
- экспериментальное подтверждение закономерностей для электрического поля точечного заряда и электрического диполя;
- экспериментальное определение величины электрической постоянной.
КРАТКАЯ ТЕОРИЯ
Два точечных заряда 
и 
взаимодействуют в вакууме между собой с силой, величина которой определяется законом Кулона:
, (2.1) где
r – расстояние между зарядами,
- электрическая постоянная.
Напряженностью электрического поля в некоторой точке называется векторная величина
, (2.2)
(2.3)
где
- сила, действующая на пробный заряд 
, помещенный в данную точку поля.
Обозначим
= 
, (2.4)
= 
.
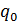Подставим (2.1) и (2.4) в (2.3)
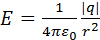. (2.5)
Справедливость закона (2.5) можно проверить, построив экспериментально линеаризованный график зависимости
. (2.6)
Электрический диполь представляет собой два жестко связанные между собой точечные заряды равные по величине и противоположные по знаку (рис. 2.1),
 |
Рис. 2.1 – Электрический диполь
При этом
, (2.7)
- расстояние между зарядами диполя.
Электрическим дипольным моментом называется векторная величина
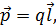(2.8)
(2.9)
Поместим пробный заряд 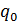на прямой, перпендикулярной оси диполя и проходящей через середину расстояния между зарядами диполя (рис. 2.2),
 |
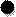
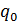
Рис. 2.2 – Электрический диполь и пробный точечный заряд
На пробный заряд действует сила
(2.10)
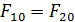(2.11)
Модуль силы равен
, (2.12)
Здесь - расстояние от зарядов диполя до точечного заряда.
На линии, проходящей через центр диполя, перпендикулярно его оси и на большом расстоянии от его центра, в случае, когда выполняется условие 
величина напряженности электрического поля равна
(2.13)
где
– электрический дипольный момент
Справедливость закона (2.13) проверяется построением экспериментального линеаризованного графика
. (2.14)
ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Эксперимент 1.
Напряженность электрического поля вычисляется по формуле
, (3.1.1)
(3.1.2)
где
– сила взаимодействия двух точечных зарядов и ,
- пробный заряд, 
Угловой коэффициент графика зависимости 
равен
, (3.1.3)
Отсюда следует, что электрическая постоянная равна
. (3.1.4)
Абсолютная погрешность 
равна
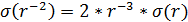, (3.1.5)
где
- расстояние между зарядами,
- абсолютная погрешность измерения расстояния между зарядами,
.
Эксперимент 2.
Напряженность электрического поля вычисляется по формуле
, (3.2.1)
, (3.2.2)
где
– сила взаимодействия двух точечных зарядов и ,
- пробный заряд, 
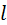- расстояние между зарядами диполя,
- расстояние между зарядами и .
Угловой коэффициент графика равен
, (3.2.3)
Отсюда следует, что электрическая постоянная равна
. (3.2.4)
Абсолютная погрешность 
равна
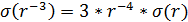, (3.2.5)
где
- расстояние между зарядами,
- абсолютная погрешность измерения расстояния между зарядами,
.
РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Вариант 7.
Таблица 4.1. Результаты измерений (эксперимент 1):
| 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | Примечание | |
| 11,111 | 6,25 | 2,777 | 2,04 | 1,563 | 1,235 | 
| |||
| ||||||||||
|
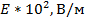
Таблица 4.2. Результаты измерений (эксперимент 2):
|
| 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | Примечание | |
| 37,037 | 15,625 | 4,629 | 2,915 | 1,953 | 1,371 |
| |||
|
| ||||||||||
|
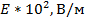
| 16,5 | 10,5 | 7,5 | 5,5 | 3,5 | 2,5 |
Таблица 4.3. Результаты измерений погрешностей:
| 1,250 | 0,370 | 0,156 | 0,080 | 0,046 | 0,029 | 0,020 | 0,014 | 0,010 |
| 9,375 | 1,852 | 0,586 | 0,240 | 0,116 | 0,062 | 0,037 | 0,023 | 0,015 |
Таблица 4.4:
| 1 эксперимент | 
| 539,957 |
|
| 8,847* 
| |
| 2 эксперимент | 
| 98,328 |
|
| 4,858*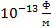 
|
ВЫЧИСЛЕНИЯ
Эксперимент 1:
1) 
2) 
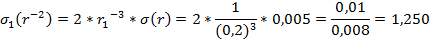
3) 
4) 
Эксперимент 2:
1)
2) 
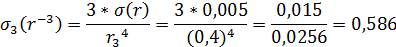
3) 
4) 
ВЫВОД
Проделав эту лабораторную работу, мы ознакомились с компьютерным моделированием электрического поля точечных зарядов, экспериментально подтвердили закономерность для электрического поля точечного заряда и электрического диполя, а также определили величины электрической постоянной.
