МАТЕМАТИКА 2
Дневная, 4 года, 1 курс
рус
Искаков С.А.
Частная производная функции 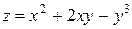 по
по  :
:
A) 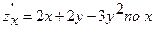 ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)&  ;
;
*****
Частная производная функции 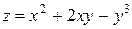 по
по  :
:
A)  ;
;
B)&  ;
;
C)  ;
;
D) 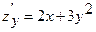 ;
;
E)  ;
;
*****
Частная производная функции  по
по  :
:
A) 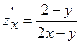 ;
;
B)  ;
;
C)&  ;
;
D) 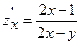 ;
;
E) 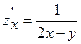 ;
;
*****
Частная производная функции  по
по  :
:
A)  ;
;
B)&  ;
;
C) 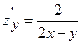 ;
;
D)  ;
;
E) 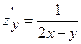 ;
;
*****
Частная производная функции  по
по  :
:
A)  ;
;
B)  ;
;
C)  ;
;
D) 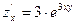 ;
;
E)&  ;
;
*****
Частная производная функции  по
по  :
:
A)  ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Интеграл  :
:
A)  ;
;
B)&  ;
;
C) 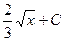 ;
;
D)  ;
;
E)  ;
;
*****
Интеграл  :
:
A)  ;
;
B) 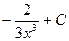 ;
;
C) 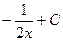 ;
;
D)&  ;
;
E)  ;
;
*****
Интеграл  :
:
A)  ;
;
B) 2  ;
;
C) 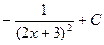 ;
;
D)&  ;
;
E)  ;
;
*****
Интеграл 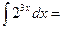 :
:
A)&  ;
;
B)  ;
;
C) 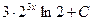 ;
;
D) 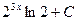 ;
;
E)  ;
;
*****
Интеграл  :
:
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Интеграл  :
:
A)  ;
;
B)& 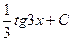 ;
;
C)  ;
;
D)  ;
;
E) 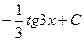 ;
;
*****
Интеграл 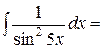 :
:
A)  ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Формула  называется формулой:
называется формулой:
A) Лейбница;
B) Коши;
C)& Ньютона-Лейбница;
D) Ньютона;
E) Даламбера;
*****
Площадь криволинейной трапеции является геометрическим смыслом:
A) производной;
B) дифференциала;
C) приращения функции;
D)& определённого интеграла;
E) частной производной;
*****
Формула Ньютона-Лейбница:
A)& 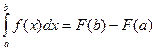
B)  ;
;
C)  ;
;
D)  ;
;
E) 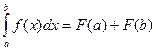 ;
;
*****
Геометрический смысл  :
:
A)& площадь криволинейной трапеции;
B) точка;
C) прямая;
D) плоскость;
E) круг;
*****
Свойство интеграла: 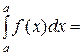 :
:
A) 
 ;
;
B)  ;
;
C)  ;
;
D)& 0;
E) 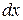 ;
;
*****
Интеграл  :
:
A) 12;
B) 1;
C)  ;
;
D) 0;
E)& 4;
*****
Интеграл  :
:
A)& 2;
B) 4;
C) ln 2;
D) 1;
E) 0;
*****
Интеграл  :
:
A) 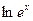 ;
;
B)  ;
;
C)  ;
;
D) 0;
E)& 1;
*****
Интеграл  :
:
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Интеграл  :
:
A) 2;
B) -2;
C)  ;
;
D) 1;
E)& 0;
*****
Интеграл 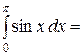 :
:
A) 0;
B) 1;
C)  ;
;
D)& 2;
E) -2;
*****
Интеграл  :
:
A)  ;
;
B)&  ;
;
C)  ;
;
D) 1;
E) 0;
*****
Интеграл  :
:
A) 0;
B)&  ;
;
C) 1;
D) 2;
E)  ;
;
*****
Площадь фигуры, ограниченной линиями  ,
,  ,
,  ,
, 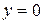 , равна:
, равна:
A) 10 кв.ед.
B) 3 кв.ед.
C) 27 кв.ед.
D)& 9 кв.ед.
E) 15 кв.ед.
*****
Площадь фигуры, ограниченной линиями  ,
, 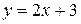 , равна:
, равна:
A)  кв.ед.
кв.ед.
B) 3 кв.ед.
C)&  кв.ед.
кв.ед.
D) 1 кв.ед.
E) 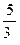 кв.ед.
кв.ед.
*****
Площадь фигуры, ограниченной линиями 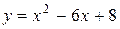 ,
,  , равна:
, равна:
A)  кв.ед.
кв.ед.
B) 3 кв.ед.
C)  кв.ед.
кв.ед.
D) 1 кв.ед.
E)&  кв.ед.
кв.ед.
*****
Площадь фигуры, ограниченной линиями  ,
, 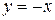 , равна:
, равна:
A) 5 кв.ед.
B)&  кв.ед.
кв.ед.
C)  кв.ед.
кв.ед.
D) 4 кв.ед.
E) 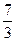 кв.ед.
кв.ед.
*****
Объём вращения фигуры, ограниченной линиями 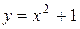 ,
, 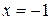 ,
,  ,
, 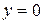 , вокруг оси ОХ равен:
, вокруг оси ОХ равен:
A)  куб.ед.
куб.ед.
B)  куб.ед.
куб.ед.
C)&  куб.ед.
куб.ед.
D)  куб.ед.
куб.ед.
E) 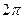 куб.ед.
куб.ед.
*****
Объём вращения фигуры, ограниченной линиями  ,
,  , вокруг оси ОХ равен:
, вокруг оси ОХ равен:
A)  куб.ед.
куб.ед.
B)  куб.ед.
куб.ед.
C)  куб.ед.
куб.ед.
D)&  куб.ед.
куб.ед.
E)  куб.ед.
куб.ед.
*****
Объём вращения фигуры, ограниченной линиями  ,
, 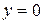 ,
, 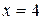 , вокруг оси ОХ равен:
, вокруг оси ОХ равен:
A)  куб.ед.
куб.ед.
B)  куб.ед.
куб.ед.
C)  куб.ед.
куб.ед.
D)  куб.ед.
куб.ед.
E)&  куб.ед.
куб.ед.
*****
Ряд  называется:
называется:
A) рядом геометрической прогрессии
B) знакочередующимся
C) тригонометрическим
D) степенным
E)& гармоническим
*****
Ряд 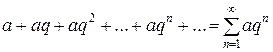 называется:
называется:
A)& рядом геометрической прогрессии;
B) знакочередующимся;
C) тригонометрическим;
D) степенным;
E) гармоническим;
*****
Ряд  , где
, где  , называется:
, называется:
A) рядом геометрической прогрессии;
B)& знакочередующимся;
C) тригонометрическим;
D) степенным;
E) гармоническим;
*****
Ряд 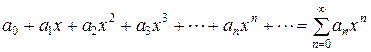 называется:
называется:
A) рядом геометрической прогрессии;
B) знакочередующимся;
C) тригонометрическим;
D)& степенным;
E) гармоническим;
*****
Если ряд  сходится, то
сходится, то  :
:
A) признак Коши;
B) признак Даламбера;
C) признак сравнения;
D) признак Лейбница;
E)& необходимое условие сходимости;
*****
Пусть даны два ряда  и
и 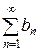 , где
, где  ,
,  и для всех
и для всех 
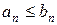 . Тогда, если ряд
. Тогда, если ряд 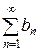 сходится, то сходится и ряд
сходится, то сходится и ряд  , а если ряд
, а если ряд  расходится, то расходится и ряд
расходится, то расходится и ряд 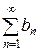 :
:
A) признак Коши;
B) признак Даламбера;
C)& признак сравнения;
D) признак Лейбница;
E) необходимое условие сходимости;
*****
Пусть дан ряд  , где
, где  и существует предел
и существует предел  . Тогда, при
. Тогда, при  ряд сходится; при
ряд сходится; при  ряд расходится, при
ряд расходится, при  вопрос о сходимости ряда остается нерешенным:
вопрос о сходимости ряда остается нерешенным:
A) признак Коши;
B)& признак Даламбера;
C) признак сравнения;
D) признак Лейбница;
E) необходимое условие сходимости;
*****
Пусть дан ряд  , члены которого являются значениями некоторой функции
, члены которого являются значениями некоторой функции 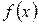 , положительной и убывающей. Тогда, если
, положительной и убывающей. Тогда, если  , то ряд сходится, если
, то ряд сходится, если 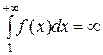 , то ряд расходится:
, то ряд расходится:
A)& признак Коши;
B) признак Даламбера;
C) признак сравнения;
D) признак Лейбница;
E) необходимое условие сходимости;
*****
Знакочередующийся ряд  сходится, если
сходится, если  и
и  :
:
A) признак Коши;
B) признак Даламбера;
C) признак сравнения;
D)& признак Лейбница;
E) необходимое условие сходимости;
*****
Разложение функции  называется рядом:
называется рядом:
A) тригонометрическим;
B) гармоническим;
C) Тейлора;
D)& Маклорена;
E) геометрической прогрессии;
*****
Разложение функции
 называется рядом:
называется рядом:
A) тригонометрическим;
B) гармоническим;
C)& Тейлора;
D) Маклорена;
E) геометрической прогрессии;
*****
Предел общего члена ряда  при
при  равен:
равен:
A)& 0;
B)  ;
;
C) 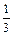 ;
;
D) 3;
E) 1;
*****
Предел общего члена ряда 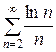 при
при  равен:
равен:
A) 1;
B)  ;
;
C) 

 ;
;
D) 2;
E)& 0;
*****
Предел общего члена ряда 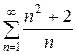 при
при  равен:
равен:
A)&  ;
;
B) 1;
C)  ;
;
D) 2;
E) 0;
*****
Предел общего члена ряда 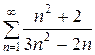 при
при  равен:
равен:
A)  ;
;
B) 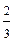 ;
;
C)&  ;
;
D) -1;
E) 0;
*****
Предел общего члена ряда  при
при  равен:
равен:
A) 0;
B) 3;
C)  ;
;
D) 1;
E)&  ;
;
*****
По признаку Даламбера у ряда  предел
предел 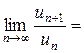 :
:
A)& 3;
B) 0;
C)  ;
;
D) 1;
E)  ;
;
*****
По признаку Даламбера у ряда 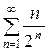 предел
предел 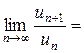 :
:
A) 2;
B) 0;
C)  ;
;
D) 1;
E)&  ;
;
*****
По признаку Даламбера у ряда  предел
предел 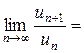 :
:
A)  ;
;
B) 0;
C)  ;
;
D) 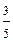 ;
;
E)&  ;
;
*****
Дифференциальное уравнение 1-го порядка с разделяющимися переменными:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  , когда корни характеристического уравнения – действительные и различные числа
, когда корни характеристического уравнения – действительные и различные числа  :
:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  , когда корни характеристического уравнения – действительные равные числа
, когда корни характеристического уравнения – действительные равные числа  :
:
A)& 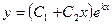 ;
;
B)  ;
;
C) 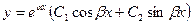 ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  , когда корни характеристического уравнения – комплексные числа
, когда корни характеристического уравнения – комплексные числа 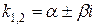 :
:
A)  ;
;
B)  ;
;
C)& 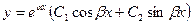 ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения 1-го порядка с разделяющимися переменными  :
:
A)  ;
;
B)  ;
;
C)  ;
;
D) 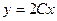 ;
;
E)&  ;
;
*****
Общий интеграл дифференциального уравнения 1-го порядка с разделяющимися переменными  :
:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E) 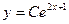 ;
;
*****
Частное решение дифференциального уравнения 1-го порядка с разделяющимися переменными  при начальных условиях
при начальных условиях  и
и 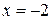 :
:
A)  ;
;
B) 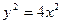 ;
;
C)  ;
;
D)  ;
;
E)& 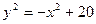 ;
;
*****
Общий интеграл однородного дифференциального уравнения 1-го порядка  :
:
A)  ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение линейного дифференциального уравнения 1-го порядка  :
:
A) 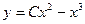 ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  :
:
A) 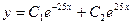 ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  :
:
A)  ;
;
B)  ;
;
C)  ;
;
D)&  ;
;
E)  ;
;
*****
Общее решение дифференциального уравнения  :
:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение уравнения  :
:
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Общее решение уравнения  :
:
A)& 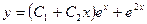 ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Результат испытания, который нельзя заранее прогнозировать, называется:
A) невозможным;
B) противоположным;
C)& случайным;
D) достоверным;
E) элементарным;
*****
Событие, которое неизбежно происходит в данном испытании, называется:
A) невозможным
B) противоположным
C) случайным
D)& достоверным
E) элементарным
*****
Событие, которое заведомо не происходит в данном испытании, называется:
A)& невозможным
B) противоположным
C) случайным
D) достоверным
E) элементарным
*****
Событие называется достоверным в данном испытании, если:
A) оно заведомо не происходит;
B)& оно неизбежно происходит;
C) его нельзя заранее прогнозировать;
D) оно не зависит от другого события;
E) оно зависит от другого события;
*****
Событие называется невозможным в данном испытании, если:
A)& оно заведомо не происходит;
B) оно неизбежно происходит;
C) его нельзя заранее прогнозировать;
D) оно не зависит от другого события;
E) оно зависит от другого события;
*****
Вероятность случайного события принимает значение:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Вероятность достоверного события:
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Вероятность невозможного события:
A)  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)&  ;
;
*****
Вероятность противоположного события:
A)  ;
;
B)&  ;
;
C) 
D) 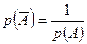 ;
;
E)  ;
;
*****
Число сочетаний из n элементов по m:
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Формула сложения вероятностей несовместных событий:
A)&  ;
;
B) 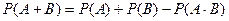 ;
;
C)  ;
;
D) 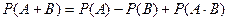 ;
;
E) 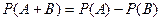 ;
;
*****
Формула сложения вероятностей событий:
A)  ;
;
B)&  ;
;
C)  ;
;
D) 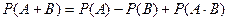 ;
;
E) 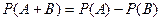 ;
;
*****
Формула умножения вероятностей независимых событий:
A)&  ;
;
B)  ;
;
C) 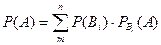 ;
;
D)  ;
;
E)  ;
;
*****
Формула умножения вероятностей событий:
A)  ;
;
B)  ;
;
C)  ;
;
D)&  ;
;
E)  ;
;
*****
Формула полной вероятности:
A)  ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Формула Бейеса:
A)  ;
;
B)&  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Формула Бернулли:
A)  ;
;
B)  ;
;
C)  ;
;
D)&  ;
;
E)  ;
;
*****
Формула математического ожидания дискретной случайной величины Х:
A) 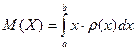 ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
Формула математического ожидания непрерывной случайной величины Х:
A)& 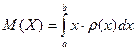 ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Формула дисперсии случайной величины Х:
A)  ;
;
B)&  ;
;
C) 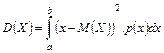 ;
;
D) 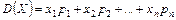 ;
;
E) 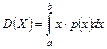 ;
;
*****
Неверное свойство математического ожидания:
A)  ;
;
B)  ;
;
C)& 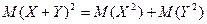 ;
;
D)  ;
;
E)  ;
;
*****
Интегральная функция распределения принимает значения:
A)  ;
;
B)&  ;
;
C) 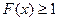 ;
;
D)  ;
;
E)  ;
;
*****
Эмпирическая функция распределения принимает значение:
A)  ;
;
B)& 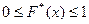 ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Формула относительной частоты, где  - объём выборки, а
- объём выборки, а  - число вариант:
- число вариант:
A)  ;
;
B) 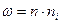 ;
;
C)& 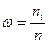 ;
;
D) 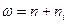 ;
;
E)  ;
;
*****
Сумма частот  :
:
A) 0;
B) 1;
C)& 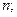
D)  ;
;
E) 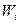 ;
;
*****
Сумма относительных частот  :
:
A) 0;
B)& 1;
C) 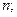 ;
;
D)  ;
;
E) 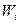 ;
;
*****
В урне 3 белых, 4 черных и 5 красных шаров. Какова вероятность вынуть из урны черный шар?
A)& 1/3;
B) 1/4;
C) 5/12;
D) 0;
E) 1;
*****
В урне 4 белых, 5 черных и 6 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется синим?
A) 1;
B) 1/3;
C) 4/15;
D)& 0;
E) 2/5;
*****
В группе деталей детали I сорта – 100, II сорта – 50, III сорта – 50 деталь. Из этой группы извлечена одна деталь. Найти вероятность того, что извлеченная деталь окажется I-го сорта.
A)&  ;
;
B)  ;
;
C)  ;
;
D)  ;
;
E)  ;
;
*****
Стрелок стреляет по мишени, разделенный на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
A) 0,2;
B) 0,9;
C) 0,35;
D) 0,45;
E)& 0,8;
*****
В денежно-вещевой лотерее на каждые 1000 билетов разыгрывается 120 денежных и 80 вещевых выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета.
A)  ;
;
B)  ;
;
C)&  ;
;
D)  ;
;
E)  ;
;
*****
В урне 6 белых и 4 черных шаров. Вынули два шара. Какова вероятность того, что оба шара белые?
A) 1/15;
B)& 1/3;
C) 0;
D) 1;
E) 4/5;
*****
В ящике 6 белых и 4 черных шаров. Найти вероятность того, что случайно выбранные 2 шара черные.
A) 0;
B) 1/2;
C)& 2/15;
D) 1/3;
E) 1;
*****
В ящике 7 не бракованных и 3 бракованных деталей. Найти вероятность того, что случайно взятые из ящика две детали окажутся бракованными.
A) 3/10;
B) 9/100;
C) 1/3;
D) 1/2;
E)& 1/15;
*****
Бросают два кубика. Какова вероятность того, что сумма выпавших очков равна 6?
A) 1/18;
B) 1/6;
C)& 5/36;
D) 1/12;
E) 1/36;
*****
Бросают два кубика. Какова вероятность того, что сумма выпавших очков равна 5?
A) 1/12;
B) 1/18;
C) 1/6;
D)& 1/9;
E) 5/36;
*****
Два охотника стреляют в зайца, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель 0,8, для второго 0,75. Какова вероятность попадания в зайца одним из стрелков?
A)& 0,95;
B) 0,8;
C) 0,75;
D) 0,35;
E) 0,7;
*****
Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель:
A) 17;
B)& 18;
C) 16;
D) 19;
E) 20;
*****
Имеется 20 ящиков однородных деталей. Вероятность того, что в одном взятом наудачу ящике детали окажутся стандартными, равна 0,75. Найти наивероятнейшее число ящиков, в которых все детали стандартные:
A) 13;
B) 14;
C)& 15;
D) 26;
E) 7;
*****
Монету подбросили три раза. Какова вероятность, что три раза монета выпала гербом вверх?
A)& 1/8;
B) 0;
C) 1/2;
D) 1/4;
E) 1;
*****
В семье 5 детей. Найти вероятность того, что среди этих детей два мальчика. Вероятность рождения мальчика принять равной 0,5:
A)  ;
;
B) 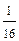 ;
;
C)  ;
;
D) 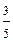 ;
;
E)&  ;
;
*****
Случайная величина характеризуется таблицей распределения:

Определить математическое ожидание:
A) 2;
B) 1,5;
C) 0;
D)& 1;
E) 0,5;
*****
Случайная величина характеризуется таблицей распределения:

Определить дисперсию.
A) 0,5;
B)& 0,6;
C) 0,7;
D) 0,8;
E) 1;
*****
Случайная величина характеризуется таблицей распределения:

Определить математическое ожидание.
A)& 2,2;
B) 2;
C) 1,5;
D) 3;
E) 2,5;
*****
Случайная величина характеризуется таблицей распределения:

Определить дисперсию.
A) 0,5;
B)& 0,56;
C) 0,3;
D) 0,4;
E) 0,6;
*****
Найти дисперсию случайной величины Х, зная закон ее распределения. 
A)& 2,01;
B) 5,75;
C) 10,85;
D) 0,95;
E) 15,5;
*****
В урне 4 белых и 8 черных шаров. Вынуто 3 шара. Какова вероятность того, что хотя бы один из них будет белым?
A) 
B) 
C)& 
D) 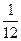
E) 
*****
Случайно выбранная кость домино оказалась не дублем. Найти вероятность того, что вторую, также взятую наудачу кость домино можно приставить к первой?
A) 
B)& 
C) 
D) 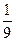
E) 
*****
Десять книг на одной полке расставляются наудачу. Определить вероятность того, что при этом 3 определенные книги окажутся поставленными рядом.
A) 
B) 
C) 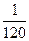
D)& 
E) 
*****
На восьми одинаковых карточках написаны соответственно числа 2, 4, 6, 7, 8, 11, 12 и 13. Наудачу берутся две карточки. Определить вероятность того, что образованная из двух полученных чисел дробь сократима.
A)& 
B) 
C) 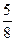
D) 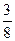
E) 
*****
Имеется 5 отрезков, длины которых равны соответственно 1, 3, 5, 7 и 9 единицам. Определить вероятность того, что с помощью взятых наудачу трех отрезков из данных пяти можно построить треугольник.
A) 
B) 
C)& 
D) 
E) 
*****
На полке в случайном порядке расставлено 20 книг, среди которых находиться трехтомник Л.Н.Толстого. Найти вероятность того, что эти тома стоят в порядке возрастания слева направо (но не обязательно рядом).
A) 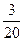
B) 
C)& 
D) 
E) 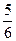
*****
Колода из 36 карт хорошо перемешана (т.е. все возможные расположения карт равновероятны). Найти вероятность того, что 4 туза расположены рядом.
A)& 
B) 
|
|
|
|
|
Дата добавления: 2017-02-25; Мы поможем в написании ваших работ!; просмотров: 667 | Нарушение авторских прав
Лучшие изречения:






