Тема 6. Эвклидово пространство.

§1. Понятие эвклидова пространства. Неравенство Коши – Буняковского.

Действительное n-мерное линейное пространство называют эвклидовым (и обозначают ), если в нем определена операция, ставящая в соответствие любым двум векторам и вещественное число, называемое их скалярным произведением (и обозначаемое · ), и при этом для любых векторов , и и любых действительных чисел выполнены аксиомы:

а – 1. · = · .

а – 2. ( + )· = · + · .

а – 3. (μ ) · =μ ( · ).

а – 4. · >0, если ≠ .

Следствия из аксиом.

1⁰. По а –1 и а – 3 .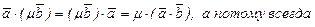

2⁰. По а - 2 и а – 1 а –1

.

3⁰. По а – 2 и а – 3 1⁰ и 2⁰.

4⁰. Из 1⁰ и т.е.

Всякий вектор эвклидова пространства имеет длину (норму). У нулевого вектора она равна нулю, у всякого другого положительна. Длина вектора в обозначается символом и по определению , где скалярное произведение называется скалярным квадратом (и обозначается ). Из определению следует, что , т.е. квадрат длины вектора равен его скалярному квадрату.

Вектор называют нормальным, если его длина равна 1. Замену вектора сонаправленным с ним нормальным вектором осуществляют умножением вектора на число и называют нормированием вектора , так что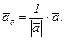

Докажем, что в для любых векторов и 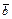имеет место неравенство

По а – 4 имеем (μ – )·(μ – ) ≥ 0 для любого действительного числа μ. Преобразуем левую часть этого неравенства: (μ – )·(μ – )= μ ·(μ – )– ·(μ – ) = = μ ·μ – μ · – ·μ + + · = μ²·( · ) – 2μ·( · ) + · . Неравенство принимает вид μ²·( · ) – 2μ ( · ) + · ≥ 0 и оно верно для любого μ. А тогда дискриминант квадратного относительно μ трехчлена не может быть положительным и верно неравенство 4( · )² – 4( · )·( · ) ≤ 0 или ( · )² ≤ ( · )·( · ), откуда после извлечения корня получаем

Из доказанного следует, что и т.к. на отрезке [0; π] функция cos j монотонная, то равенство

cos j = 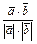(16)

верно только при одном значении j, которое по определению называют углом между n-мерными векторами и .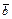

§2. Ортонормированный базис. Матрица Грама. Скалярное произведение векторов. Процесс ортогонализации.

Векторы и из называют ортогональными, если их скалярное произведение равно нулю. Из соотношения (16) следует, что для ортогональности ненулевых векторов необходимо и достаточно, чтобы угол между ними был равен . Нулевой вектор полагают ортогональным любому вектору.

В система векторов называется ортогональной, если любые два ее вектора ортогональны, и – нормальной, если все ее векторы нормальны.

Если система векторов ортогональна и ни один из векторов системы не является нулевым, то, нормируя эти векторы, получим так называемую ортонормированную систему векторов.

Если система векторов S(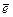) = () ортонормированная, то для всех k и s от 1 до n имеем 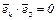при k ≠ s, т. к. векторы и ортогональны, и 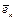· 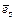= 1 при k = s, т.к.

В любая ортонормированная система S(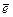) из n векторов линейно независима, т. е. образует ортонормированный базис. Действительно, умножив на скалярно обе части равенства 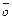, для любого k от 1 до n получим 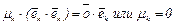и система S(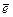) линейно независима по определению.

Каким бы ни был базис S(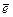), всевозможные попарно скалярные произведения базисных векторов – числа запишем в виде квадратной матрицы:

Матрица Г называется матрицей Грама базиса S(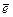). В силу коммутативности скалярного умножения верно равенство и, следовательно, матрица Грама не меняется при транспонировании, т.е. является симметрической.

В некотором произвольном базисе S(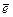) = () вычислим скалярное произведение векторов:

Базис ортонормирован тогда и только тогда, когда его матрица Грама – единичная матрица. Поэтому для ортонормированного базиса в R_n скалярное произведение векторов вычисляется по формуле:

т.е.

.

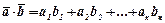Из этой формулы следует, что в ортонормированном базисе 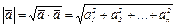, угол φ между векторами и 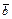находят из соотношения

а условие ортогональности этих векторов имеет вид:

Примером ортонормированного базиса в R_n является система ортов , где для всех k и s от 1 до n имеем:

Если произвольный вектор разложен по ортонормированному базису, то, умножив скалярно обе части разложения на , для каждого k от 1 до n получим число , называемое проекцией вектора 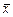на направление вектора .

В существовании ортонормированного базиса можно также убедиться, применив к произвольному базису из R_n так называемый метод ортогонализации.

Задача 0.61. В пространстве R₄ векторы = (–1, 0, 2, 1)^T, 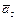= (0, –2, 1, 1)^T, = (1, 1, –1, 0)^T и
= (2, 1, 0, –1)^T образуют базис. С помощью векторов этого базиса построить ортонормированный базис.

Решение. Построим в R₄ ортогональный базис 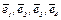. Пусть .

(1) Полагаем . Действительное число a подберем так, чтобы выполнялось условие

Обе части равенства (1) умножим скалярно на 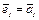. Получим: 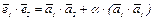или
0 = 3 +6a, a = – 0,5. И тогда или

(2) Полагаем Числа и подберем так, чтобы выполнялись условия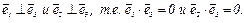

Умножим скалярно обе части равенства (2) сначала на а затем на

а)

б)

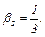
Следовательно, или

(3) Полагаем 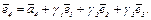Числа подберем так, чтобы выполнялись условия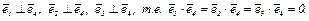

Умножим скалярно обе части равенства (3) отдельно на затем на затем на .

а)

б)

в)

Следовательно,

Остается нормировать векторы , разделив каждый на его длину.

Т.к. и то векторы образуют ортонормированный базис.

Ответ:

Задача 0.62. Дана матрица перехода от ортонормированного базиса к базису . Доказать, что базис ортонормированный.

Доказательство. Векторы системы имеют вид:

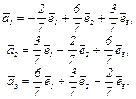
Т.к. detT = 1 ≠ 0, то векторы линейно независимы и образуют базис. Векторы этого базиса нормальны, т.к. и попарно ортогональны, т.к. 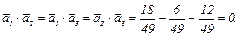Следовательно, базис ортонормированный.